
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие дифференциала функции
Пусть функция f дифференцируема в точке x, т.е. пусть ее приращение может быть записано в виде
где
Таким образом, дифференциал функции равен произведению ее производной на приращение аргумента. Дифференциал- от латинского слова differentio- разность. Теорема 2. Если функция f дифференцируема в точке x, причем производная от f не обращается в нуль в этой точке, то дифференциал функции f и ее приращение являются при
Доказательство. Мы имеем
Поскольку дифференциал эквивалентен при Заметим, что
Заметим, что дифференциал может быть и больше, чем приращение функции (это будет иметь место, если Пример 5. Найдем приращение и дифференциал функции Решение. Так как При Приращение же функции Найдем дифференциал для функции f, где f (x)= x. Так как Из формулы
Запись
Глава 2. Применение производной к решению задач Исследование функции
Дифференциальное исчисление широко используется при исследовании функций. С помощью производной можно найти промежутки монотонности функции, ее экстремальные точки, наибольшие и наименьшие значения.
Возрастание и убывание функций. Как известно функция, заданная на множестве
Если
то функция Аналогично определяются понятия убывающей и невозрастающей функций. Теорема 3. Если функция Доказательство. Рассмотрим две любые точки
где точка Поскольку оба множителя правой части равенства (18) положительны (
а значит, и
Итак, Теорема 4. Если функция Доказательство этой теоремы аналогично. Пример 6. Докажем, что функция Решение. Имеем
Так как при любом Определение 7. Пусть функция то Точки максимума называют точками экстремума. [2, c. 85] Определение 8. Точки, в которых производная равна нулю или не существует, называют критическими (иногда точки, где производная равна нулю, называют стационарными). [2, c. 86] Теорема 5. пусть функция
Если на Доказательство. Пусть производная По условию функция Таким образом, в
Это означает, что Рассмотрим случай, когда производная не меняет знака при переходе через точку Остальные два случая рассматриваются аналогично. Теорема доказана. [2, c. 101] Таким образом, чтобы исследовать функцию Пример 7. Исследуем на экстремум функцию Решение. Имеем
Приравняв производную к нулю, находим
|
||||||
|
Последнее изменение этой страницы: 2021-04-20; просмотров: 116; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.208.117 (0.021 с.) |
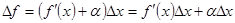 ,
, . Это приращение состоит из двух слагаемых:
. Это приращение состоит из двух слагаемых: 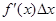 , пропорционального
, пропорционального 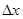 , и
, и 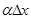 , зависимость которого от
, зависимость которого от 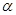 тоже зависит от
тоже зависит от 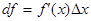 . (19)
. (19)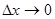 эквивалентными бесконечно малыми, т.е.
эквивалентными бесконечно малыми, т.е.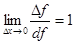 .
.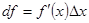 и
и 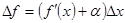 . Так как
. Так как 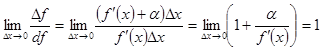 .
.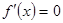 , то дифференциал функции f в точке
, то дифференциал функции f в точке 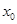 равен нулю. В этом случае
равен нулю. В этом случае  и поэтому приращение является бесконечно малой более высокого порядка, чем
и поэтому приращение является бесконечно малой более высокого порядка, чем 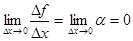 .
. ). [2, c. 14]
). [2, c. 14]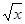 при x = 1,
при x = 1, 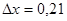 .
.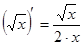 , то
, то 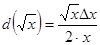 .
.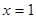 ,
, 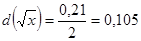 .
.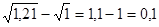 .
.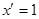 , то
, то 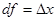 . Поскольку для этой функции f (x)= x, то пишут
. Поскольку для этой функции f (x)= x, то пишут 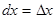 . Таким образом, считают дифференциал независимой переменной равным приращению этой переменной. В соответствии с этим формулу (17) обычно записывают в следующем виде:
. Таким образом, считают дифференциал независимой переменной равным приращению этой переменной. В соответствии с этим формулу (17) обычно записывают в следующем виде: 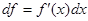 . В приложениях функции обычно записывают в виде
. В приложениях функции обычно записывают в виде 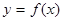 , обозначая буквой x аргумент, а буквой y - значение функции. При такой записи производную от функции f обозначают
, обозначая буквой x аргумент, а буквой y - значение функции. При такой записи производную от функции f обозначают 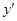 или
или 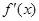 . Соответственно дифференциал функции y = f (x) обозначают
. Соответственно дифференциал функции y = f (x) обозначают 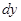 , причем употребляют как запись
, причем употребляют как запись 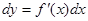 , так и запись
, так и запись 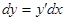 .
.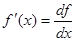 .
.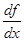 (или
(или 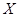 , называется возрастающей на этом множестве, если для любых
, называется возрастающей на этом множестве, если для любых 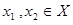 , таких, что
, таких, что 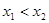 , имеем
, имеем 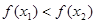 :
: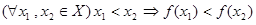 .
.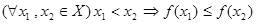 ,
,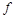 называется неубывающей на множестве
называется неубывающей на множестве 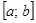 , а ее производная положительна на интервале
, а ее производная положительна на интервале 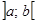 , то
, то 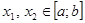 , такие, что
, такие, что 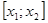 выполняется условие теоремы Лагранжа, то
выполняется условие теоремы Лагранжа, то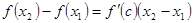 , (18)
, (18)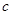 лежит между
лежит между 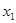 и
и 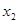 .
.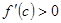 по условию,
по условию, 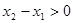 в силу выбора точек), то
в силу выбора точек), то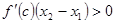 , (19)
, (19)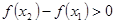 .
.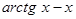 убывает на всей числовой прямой.
убывает на всей числовой прямой.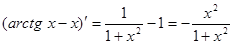 .
.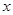 выполняется неравенство
выполняется неравенство 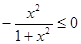 и, кроме того, равенство
и, кроме того, равенство 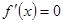 выполняется только в одной точке
выполняется только в одной точке 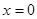 , то на всей числовой прямой
, то на всей числовой прямой 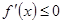 , причем
, причем 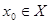 и непрерывна в этой точке. Если существует такая окрестность точки
и непрерывна в этой точке. Если существует такая окрестность точки 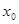 , что для всех точек
, что для всех точек 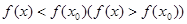 ,
,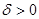 , такое, что функция
, такое, что функция 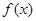 непрерывна на отрезке
непрерывна на отрезке 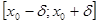 , дифференцируема на интервалах
, дифференцируема на интервалах 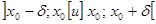 , причем производная данной функции сохраняет знак на каждом из этих интервалов.
, причем производная данной функции сохраняет знак на каждом из этих интервалов.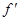 положительна на интервале
положительна на интервале 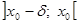 и отрицательна на
и отрицательна на 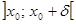 . Докажем, что
. Докажем, что 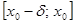 , дифференцируема в интервале
, дифференцируема в интервале 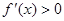 . Значит по теореме 1 функция
. Значит по теореме 1 функция 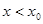 , где
, где 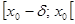 , следует
, следует 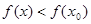 . Аналогично устанавливаем, что функция
. Аналогично устанавливаем, что функция 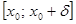 , а поэтому из неравенства
, а поэтому из неравенства 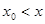 , где
, где 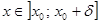 , следует
, следует 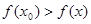 .
.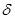 - окрестности точки
- окрестности точки 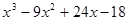 .
.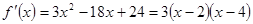 .
.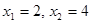 . При переходе через точку
. При переходе через точку 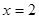 производная меняет знак с «+» на «-», значит, в этой точке функция имеет максимум. При переходе через точку
производная меняет знак с «+» на «-», значит, в этой точке функция имеет максимум. При переходе через точку 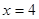 производная меняет знак с «-» на «+», значит, в этой точке функция имеет минимум. Имеем
производная меняет знак с «-» на «+», значит, в этой точке функция имеет минимум. Имеем 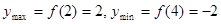 .
.


