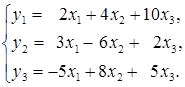Необходимое и достаточное условия идентифицируемости.

Выполнение условий идентифицируемости модели проверяется для каждого уравнения системы.

Обозначим через H – число эндогенных переменных в уравнении, а через D – число экзогенных (предопределенных) переменных, отсутствующих в уравнении, но присутствующих в системе. Тогда необходимое условие идентификации отдельного уравнения принимает вид:

– уравнение идентифицируемо,          если H = D + 1;

– уравнение неидентифицируемо,      если H > D + 1;

– уравнение сверхидентифицируемо, если H < D + 1.

Если необходимое условие выполнено, то далее проверяется достаточное условие идентификации.

Достаточное условие идентификации. Уравнение идентифицируемо, если определитель матрицы, составленной из коэффициентов при переменных, отсутствующих в исследуемом уравнении, не равен нулю, и ранг этой матрицы не менее числа эндогенных переменных системы без единицы.

Пример 1. Требуется:

1. Оценить следующую структурную модель на идентификацию:

Решение:

Исследование модели на идентифицируемость. Модель имеет три эндогенные (у1, у2, у3) и три экзогенные (х1, х2, х3) переменные.

Проверим каждое уравнение системы на необходимое и достаточное условия идентификации.

а) Первое уравнение.

Необходимость: эндогенных переменных – H = 2 (y1, y3), отсутствующих экзогенных – D = 1 (х2).

Выполняется необходимое равенство: 2 = 1+1, следовательно, уравнение точно идентифицируемо.

Достаточность: в первом уравнении отсутствуют у2 и х2. Построим матрицу из коэффициентов при них в других уравнениях системы

Уравнение	Отсутствующие переменные
	у2	x2
Второе	–1	a22
Третье	b32	0

 

Определитель матрицы Det A = –1·0 – b32 a22 ≠ 0.

Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и первое уравнение точно идентифицируемо.

б) Второе уравнение.

Необходимость: эндогенных переменных – H = 3 (y1, y2. y3), отсутствующих экзогенных – D = 2 (х1, х3).

Выполняется необходимое равенство: 3 = 2+1, следовательно, уравнение точно идентифицируемо.

Достаточность: во втором уравнении отсутствуют х1 и х3. Построим матрицу из коэффициентов при них в других уравнениях системы:

 

Уравнение	Отсутствующие переменные
	х1	х3
Первое	a11	a13
Третье	а31	а33

 

Определитель матрицы Det A = a11 a33 – a31 a13 ≠ 0.

Определитель матрицы не равен 0, ранг матрицы равен 2, следовательно, выполняется достаточное условие идентификации, и второе уравнение точно идентифицируемо.

Аналогично доказывается, что и третье уравнение точно идентифицируемо. Следовательно, исследуемая система точно идентифицируема и может быть решена косвенным методом наименьших квадратов.

Пример 2. Исходя из приведенной формы модели уравнений

найти структурные коэффициенты модели.

Решение:

1) из третьего уравнения приведенной формы выразим х2 (так как его нет в первом уравнении структурной формы)

х2=(y3+5х1−5х3)/8.

Данное выражение содержит переменные y3, х1 и х3, которые входят в правую часть первого уравнения структурной формы модели (СФМ). Подставим полученное выражение х2 в первое уравнение приведенной формы модели (ПФМ)

y1= 2x1 + 4(y3+5х1−5х3)/8+ 10x3.

Откуда получим первое уравнение СФМ в виде

y1= 0,5y3 + 4,5x1+ 7,5x3.

2) во втором уравнении СФМ нет переменных х1 и х3. Структурные параметры второго уравнения СФМ можно будет определить в два этапа.

Первый этап: выразим х1 в данном случае из первого или третьего уравнения ПФМ. Например, из первого уравнения

x1=(y1 - 4x2 - 10x3)/2.

Подстановка данного выражения во второе уравнение ПФМ не решило бы задачу до конца, так как в выражении присутствует х3, которого нет в СФМ.

Выразим х3 из третьего уравнения ПФМ

x3=(y3+5x1-8x2)/5.

Подставим его в выражение для х1

x1=0,5y1 - 2x2 - 5(y3+5x1- 8x2)/ 5=0,5y1 +6x2 - y3 - 5x1.Откуда

x1=(0,5y1 +6x2 - y3)/6.

Второй этап: аналогично, чтобы выразить х3 через искомые y1, y3 и х2, заменим в выражении х3 значение х1 на полученное из первого уравнения ПФМ

x3= (5(y1 - 4x2 - 10x3)/2- 8x2+ y3)/5=0,5y1–3,6x2 - 5x3+0,2y3.

Следовательно,

x3= (0,5y1 – 3,6x2 +0,2y3)/6.

Подставим полученные х1 и х3 во второе уравнение ПФМ

y2=3(0,5y1 +6x2 - y3)/6 – 6x2+ 2(0,5y1 – 3,6x2 +0,2y3)/6.

В результате получаем второе уравнение СФМ

y2=0,416y1 -0,434y3 – 4,2x2.

3) из второго уравнения ПФМ выразим х2, так как его нет в третьем уравнении СФМ

x2=(3x1 –y2+ 2x3)/6.

Подставим полученное выражение в третье уравнение ПФМ

y3= -5x1+ 8(3x1 –y2+ 2x3)/6+ 5x3.

В результате получаем третье уравнение СФМ

y3= –1,336y2- x1+ 7,664x3.

Таким образом, СФМ примет вид

y1= 0,5y3 + 4,5x1+ 7,5x3;

y2=0,416y1 -0,434y3 – 4,2x2;

y3= –1,336y2- x1+ 7,664x3.