
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перечень литературы и наглядных пособийСтр 1 из 4Следующая ⇒
Вопросы лекции
1. Основные законы и правила алгебры логики 2. Способы представления ФАЛ 3. Минимизация переключательных функций 4. Комбинационные схемы.(автомат Мили), их анализ и синтез. Понятие о конечном автомате (автомат Мура)
Перечень литературы и наглядных пособий 1. [ 7 ] стр. 50 – 79 2. [ 2 ] стр. 177- 199 Перечень заданий на самостоятельную подготовку.
1. Изучить метод минимизации при помощи диаграмм Вейча
[ 1 ] стр. 50 – 79 [ 2 ] стр. 177- 199 [ 6 ] стр. 33 – 62
Время - 1 час.
Преподаватель:
Логические основы ЭВМ. Понятие о цифровом автомате.
Преобразование информации в ЭВМ осуществляют цифровые автоматы (ЦА), которые бывают двух типов А) без памяти (примитивные автоматы) или комбинационные схемы (КС), автоматы Мими, используемые для построения простейших узлов и цифровых блоков ЭВМ.
-информаторы; -дешифраторы; -суматоры; -преобразователи кодов; -схемы контроля и т.п.;
б) с памятью (покопливающиеся или последовательные схемы, ЦА, полный автомат (автомат Мура). Они используются для построения - триггерных устройств; - регистров; - счетчиков; - распределителей импульсов и др.

  В КС выходные сигналы (результат преобразования информации) зависит только от комбинации сигналов, подаваемых на вход в данный момент времени. Т.к. память отсутствует, то действующие на входе сигналы не сохраняются. В КС выходные сигналы (результат преобразования информации) зависит только от комбинации сигналов, подаваемых на вход в данный момент времени. Т.к. память отсутствует, то действующие на входе сигналы не сохраняются.
Y(t) = F (X(t),t);
В ЦА результат преобразования информации (входные сигналы) зависят не только от значений сигналов на входе в данный момент времени, но и от последовательности предыдущих составляющих входных и выходных т.е. от внутренних состояний схемы

Переход от условий работы ЦА к его функционированию с памятью аппарата логики или булевой алгебры, которая является одной из ветвей мат. логики.
Функции, описывающие работу ЦА, показываются переключательными, т.к. они хорошо отражают в аналитической форме закон функционирования электронных схем, состоящих из элементов с двумя устойчивыми состояниями и осуществляющие переключение из одного состояния в другое.
3. Основные понятия алгебры логики. Впервые идею о возможности формировать процесс логическим рассуждении высказал Аристотель. Позже к ней вернулся Лейбниц. Однако по-настоящему математическая логика была разработана Булем (1815- 1864 г.г.) Его работы развили Э.Пост, К. Шеннон, В. Глушков, С. Яблонский и др.
Логика – это наука о законах и формах мышления.
Математическая логика – наука о применении матаматических методов для решения логических задач. Она служит теоретической основой построения ЭВМ и цифровых устройств. Основное понятие алгебры логики – высказывания. Высказывание – любое утверждение, в отношении которого имеет смысл утверждать истинно оно или ложно. Все теоремы и основы являются высказывания.
Высказывания м. б. - простыми – не зависят от других высказывания - сложные – образующиеся из двух и более простых высказываний.
Простые высказывания являются логическими переменными (или логическими аргументами), а сложные – логическими функциями этих переменных. Простые высказывания обозначаются строчными буквами, сложные – прописными. Высказывания оценивают только по их истинности или ложности.
Х Є {0,1} Высказывание абсолютно истинно, если логическая величина принимает значение Х=1 при любых условиях Например «Земля планета Солнечной системы» Взысказывание абсолютно ложно, если логическая величина принимает значение х=0 при любых условиях. Например «Земля спутник Марса» Кроме того, существуют взысказывания, которые могут быть истинными или ложными в зависимости от определенных условий (например» на улице идет дождь»)
Логическая функция – (функция алгебры логики) это функция вида F (X1 X2 … XN), принимающие значение, равна 0 или1 на наборе логических переменных X1 X2 … XN называется набором аргументов. Упорядоченной набор аргументов, путем присвоения им номеров, приводит к упорядоченной последовательности путей и единицу, называемой кортежем.
Например: для F (X1 X2 X4) При Х1=0, Х2=1, Х3=1 и Х4= 1 Тогда для данного кортежа аргументов функция м.б. записана так. (0,1,1,1) Менять местами в кортеже 0 и1 нельзя, т.к. будет другой кортеже аргументов и ему будет соответствовать другая ФАЛ. Кортеже удобно изображать в виде n- значного двоичного числа, каждый разряд которого равен значению одного из аргументов (наз. 0111) Тогда количество возможных различных наборов (кортежей) равно количеству чисел, которые м.б. изображены с помощью n двоичных разрядов, т.е. k = 2n Т.к. ФАЛ принмает значение 0 или 1, то общее число ФАЛ N=2k Следовательно, Общее число функций, Которые могут быть образованы от n аргументов, равно n N=22
Одноместная ФАЛ
Табл. 1
n 2 N= 2 K=2n=22=4 N = 22 =22 = 16
1. Константа нуля F1 = 0 F1 = всегда ложна, Независимо от высказывания (обозначается F0)
F2(X1 X2) = X1*X2 = X1&X2 = X1^X2
F4= истина только в том случае, когда Х1 истина, от Х2 не зависит. Элемент задержки Х1
F5 – истина только, когда Х2 истина, а Х1 ложна.
F6 истина только тогда, когда Х2 истина, от Х1 не зависит Элемент задержки Х2
7. Неравнозначность или сложение по модулю 2 (Н2)
F7 = истина тогда, когда истина или Х1, или Х2 в отдельности.
8. Дизъюнкция – логическое сложение
F8 истинно тогда, когда истинны или Х1 или Х2 или обе переменные вместе F8= (X1,X2) = X1+X2= X1^X2
9. Функция Пирса (Вебба)
F9= (X1,X2)= X1^X2 = X1*X2 = X1 X2 = X1 0 X2 Др. название стрелка Пирса, функция ИЛИ – НЕ, отрицание конъюнкции Математически Пирс и Вебб, независимо друг от друга изучавшие свойства этой функции, создали алгебру, названную алгеброй Пирса (Вебба)
10. Равнозначность
F10 истина только тогда, Когда переменные равнозначны (эквивалентны друг другу.
Другое название эквивалентность.
11. Инверсия X2
F11 истина только тогда, когда X2 ложна и ложна, когда Х2 истина
12. Импликация Х2 в X1
F12 истина только тогда Х2 истина, а Х1 ложна
Если Х2 истина то Х1 ложно (следствии за истиной лжи) Логическое следование.
13.Инверсия Х1
F13 истина тогда Х1 ложно и ложна, когда Х2 истина.
14. Импликация Х1 вХ2
F14 ложна тогда когда X1 истина, и Х2 ложна
15. Функция Шеффера
F15 (X1,X2) = X1/X2 = X1& X2 = X1^X2
F15 ложна только тогда, когда Х1 и Х2 одновременно истины Другое название штрих Шеффера, И- НЕ Немецкий математик Шеффер на основе этой ФАЛ создал алгебру (Шеффера)
16. Константа единицы F16 = 1
F16 всегда истина, независимо от высказывания.
Все функции в таблице 2 элементарные функции.
Аксиомы алгебры логики Х*1=Х Х^1=1
- возможность выражать дизъюнкцию через конъюнкцию и отрицание - конъюнкцию через дизъюнкцию и отрицание
Представление ФАЛ
1. Основные определения
Существует много способов описания ЦА.
- табличный - с помощью ФАЛ (аналитический); - секвенциальное - с помощью граф-схем и логических схем алгоритмов и др.
Первый способ представлен в табл. 1 и Табл. 2. В них каждому из возможных наборов переменных ставится в соответствие значение функции (0 или 1) Этот способ нагляден и может быть применен для представления функции любого числа переменных. Однако для больших n такая форма уже не компактна, т.к. таблица будет громоздкой. Кроме того, в табличной форме преобразование данных затруднено.
Таблица, описывающая работу ЦА, называется таблицей истинности. Ее построение является чаще всего лишь первым этапом при проектировании сложных ЦА, в том числе и ЭВМ. Проще выглядит аналитическая запись переключательной функции в виде формул.
Прежде рассмотрим элементарные понятия
Терм – языковое выражение, обозначающее объекты. Симтатически характеризуется тем, что термы можно подставлять вместо переменных в другие выражения языка – термы и формулы, получая при этом соответственно новые термы и формы.
Минтермом – или конституэнтой еденицы называют функцию принимающие еденичное значение при фиксированном наборе аргументов. Макстермом – или конституэнтой нуля называют функцию принимающую нулевое значение при фиксированном наборе аргументов.
Например
Суммарное число минтермов и макстермов совпадает с числом наборов различных аргументов.
Например Х1^Х2^Х3 или Х1*Х2*Х3*Х4 r = 3 r = 4 Число переменных, составляющих элементарную конъюнкцию (дизъюнкцию), называется ее рангом r Рассмотрим различные формы аналитической записи переключательной функции. Нормальные формы - представляют лишь дизъюнкции элементарных конъюнкций или конъюнкцию элементарных конъюнкций.
Нормальная форма, представляет дизъюнкций элементарных конъюнкций
Fдиф. (Х1,Х2,Х3)= Х1*Х2*Х3^Х1*Х2, называется ДИФ нормальная форма, представленная конъюнкций элементарных дизъюнкций
Набора |
Аргументы | F(X1,X2,X3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Х1 | Х2 | Х3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0 | 0 | 0 | 0 | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 0 | 0 | 1 |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 0 | 1 | 0 |   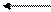 1 1
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 0 | 1 | 1 | 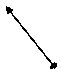 0 0
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 1 | 0 | 0 | 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 1 | 0 | 1 |  0 0
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | 1 | 1 | 0 | 
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | 1 | 1 | 1 | 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 СНДФ представления переключательных функций – это запись функции в виде дизъюнктивной, (сумма произведений) для которых значение функции равно 1, т.е. в виде дизъюнкции минтермов. Каждая конъюнкция этой дизъюнкции включает каждую переменную только один раз в прямом или инверсном виде.
СНДФ представления переключательных функций – это запись функции в виде дизъюнктивной, (сумма произведений) для которых значение функции равно 1, т.е. в виде дизъюнкции минтермов. Каждая конъюнкция этой дизъюнкции включает каждую переменную только один раз в прямом или инверсном виде.
Алгоритм перехода от табл. Представления ПФ к СДНФ следующий:
- Составить минтермы для строк таблицы истинности, для которой ПФ= 1. Если значение переменной Хi = 0, то в минтерме записывается отрицание этой переменной.
- Записать дизъюнкцию составленных минтермов, которая и представляет ПФ в СДНФ.
Это правило – правило записи ПФ по единицам для Табл.3





 FСДНФ (Х1,Х2,Х3) = Х1*Х2*Х3^ Х1*Х2*Х3^ Х1*Х2*Х3^ Х1*Х2*Х3 (6)
FСДНФ (Х1,Х2,Х3) = Х1*Х2*Х3^ Х1*Х2*Х3^ Х1*Х2*Х3^ Х1*Х2*Х3 (6)
СДНФ – это запись функции в виде конъюнкции дизъюнкции (произведения суммы), для которых значение функции = 0.
|
|
Алгоритм перехода - от таблицы ПФ к ее СКНФ.
1. Составить макстермы для строк табл. истинности, на которых функция = 0. Если значение переменной Хi= 1, то в макстерме записывается отрицание этой переменной
2. Записать конъюнкцию составных макстермов, которая и есть ПФ в СДНФ.
Это правило – правило записи ПФ по нулям.
Для табл. 3





 FСДНФ(Х1,Х2,Х3) = (Х1^Х2^Х3) (Х1^Х2^Х3) (Х1^Х2^Х3) (Х1^Х2^Х3) (7)
FСДНФ(Х1,Х2,Х3) = (Х1^Х2^Х3) (Х1^Х2^Х3) (Х1^Х2^Х3) (Х1^Х2^Х3) (7)
Применив операцию инвертирования к (7), получим связь между СДНФ и СКНФ ПФ
|
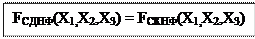
Не полностью определенные ПФ - ПФ, для которых не определено их значение хотябы на одном наборе переменных (аргументов)
Доопределение такой ПФ, (т.е. положение = 0 или 1) производится на разных этапах обработки информации в зависимости от конкретной задачи.
Иногда при доопределении рассматривают 2 варианта СКНФ и 2 варианта СДНФ.
Конституенты СДНФ и СКНФ, соответствующие наборам аргументов, на которых ПФ не определена, называют условными.
Конституенты разложения 1, вошедшие в СДНФ, и Конституенты разложения 0, вошедшие в СКНФ, называют обязательными, е\а не вошедшие - запрещенными коституентами.
СДНФ и СКНФ широко используют при синтезе и анализе ложных схем ЭВМ.
Аналитический способ
СДНФ и СКНФ содержат, в отличии от нормальной, дизъюнкции и конъюнкции только максимального ранга r.
Это дает возможность производить переход по следующим правилам.
 Правило 1. для перехода от произвольной ДНФ К- го ранга (К<r) к СДНФ r- го ранга необходимо конъюнкции ДНФ последовательно умножать на логическое выражение (Хi^Xi) где,
Правило 1. для перехода от произвольной ДНФ К- го ранга (К<r) к СДНФ r- го ранга необходимо конъюнкции ДНФ последовательно умножать на логическое выражение (Хi^Xi) где,
Xi – она из переменных, не вошедшая в данную конъюнкцию.
Число таких преобразований для каждой конъюнкции д.б. (r-k)
Пример. Преобразовать ДНФ
FСДНФ(Х1,Х2,Х3) = Х1*Х2^Х3 в СДНФ
R = 3-го ранга

 А) Х1*Х2(Х3^Х3) = Х1*Х2*Х3^ Х1*Х2*Х3
А) Х1*Х2(Х3^Х3) = Х1*Х2*Х3^ Х1*Х2*Х3



 Б) Х3(Х1^Х1)= Х3*Х1^Х3*Х1 – 1-е преобразование
Б) Х3(Х1^Х1)= Х3*Х1^Х3*Х1 – 1-е преобразование



 В) (Х3*Х1^Х3*Х1)(Х2^Х2) = Х1*Х2*Х3^Х1*Х2*Х3^ Х1*Х2*Х3^ Х1*Х2*Х3 = 2-е преобразование.
В) (Х3*Х1^Х3*Х1)(Х2^Х2) = Х1*Х2*Х3^Х1*Х2*Х3^ Х1*Х2*Х3^ Х1*Х2*Х3 = 2-е преобразование.




 Г) FСДНФ(Х1,Х2,Х3) = Х1*Х2*Х3^ Х1*Х2*Х3^ Х1*Х2*Х3^ Х1*Х2*Х3^ Х1*Х2*Х3
Г) FСДНФ(Х1,Х2,Х3) = Х1*Х2*Х3^ Х1*Х2*Х3^ Х1*Х2*Х3^ Х1*Х2*Х3^ Х1*Х2*Х3
 Правило 2: Для перехода от произвольной КНФ к СКНФ r-го ранга необходимо дизъюнкции, входящие в КНФ к-го ранга последовательно симулировать с логическим выражением Хi*Хi (Х^0) = Х
Правило 2: Для перехода от произвольной КНФ к СКНФ r-го ранга необходимо дизъюнкции, входящие в КНФ к-го ранга последовательно симулировать с логическим выражением Хi*Хi (Х^0) = Х
Где Хi - одна из переменных, не входящая в данную дизъюнкцию. Число преобразований для каждой дизъюнкции д.б. (r-k)
Минимизация ПФАЛ.
Минимальной формой представления ПФ называюттакую, которая не допускает дальнейшее упрощение
Минимизация ПФАЛ – это процесс получения минимальной нормальной формы.
При минимизации исходят из требования минимальных затрат оборудования при физической реахлизации ПФАЛ, т.к. каждой элементарной логической функции соответствует определенной логической элемент.
Как правило, минимизация сигнала осуществляется в базисе и, ИЛИ-НЕ, а затем, с помощью специальных методов переходт к заданному базису.
Методы:
- последовательного исключения переменных с помощью законов, правил и аксиом алгебры логики.
- метод Кванта – для ПФ невысокого порядка при условии, что исходные функции заданы в СДНФ.
- минимизирующих карт Карно – для функций небольшого числа переменных
- метод диаграмм Вейча – разновидность метода Карно.
Диаграмма Вейча
Количество клеток K = 2n n – число аргументов.
|

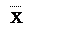
  X*Y X*Y
|
 X*Y X*Y
| ||||
 X*Y X*Y
| X*Y |
Каждому кортежу своя клетка
Содержимое клетки – конъюнкция переменных
|

 Пример 1. F(X,Y) = XY^XY
Пример 1. F(X,Y) = XY^XY
|


|

| ||||||||

|
|
 Д-но: F(X,Y) = X(Y^Y)
Д-но: F(X,Y) = X(Y^Y)










 Пример 2. F(x,y) =XY^ XY^ XY^XY=(XY^ XY)(XY^ XY) = X(Y^Y)^Y(X^X)=X^Y
Пример 2. F(x,y) =XY^ XY^ XY^XY=(XY^ XY)(XY^ XY) = X(Y^Y)^Y(X^X)=X^Y
 |

|

| ||||||||

|
|
|
|
XYZ | 110 XYZ | 100 XYZ | 101 XYZ | ||
| 011 XYZ | 010 XYZ | 000 XYZ | 001 XYZ |
|


Можно инвертировать как развертку боковой поверхности цилиндра.
Поэтому единицу в крайнем левом и правом столбцах находятся рядом.


|
A= log2Q
Где Q – число рядом стоящих единиц, образующих импликатуру.
А- целое число, показывающее, на сколько переменных в импликанте меньше, чем в конституенте 1.
Импликатой ФАЛ
F(*) называют любую другую ФАЛ q(*) меньшей сложности, которая на тех наборах аргументов, на которых F(*)=0, обязательно обращается в 0, (т.е. если F(*)=0,то q(*)=0); а на тех наборах аргументов, на которых F(*)=1, импликанта обращается либо в 0, либо в 1. т.е. если F(*)=1,то q(*)=0^q(*)=1
Если а=1, то Q=2 – охватывается контуром две единицы.
Если а=2, то Q=4 – четыре единицы.
В первом случае в импликанте будет на одну, а во втором на два аргумента меньше, чем в конституенте единицы.








 Пример 3. F(x,y,z) = XYZ^ XYZ^ XYZ^ XYZ^ XYZ
Пример 3. F(x,y,z) = XYZ^ XYZ^ XYZ^ XYZ^ XYZ


| ||||
 | ||||
|

| 


| |||||||||||
 
|
|
|
|


|
|
Второй контур охватывает четыре «1». Импликанта = Z
|
|

 Д-но:
Д-но:

 XY YZ = XZ м.в. YZ тогда
XY YZ = XZ м.в. YZ тогда




 X(t) = X1 X2 X3... XN
X(t) = X1 X2 X3... XN 
 Y(t) =
Y(t) = 

 Считают, что высказывания = 1, если оно истинно и = 0, если ложно. Т.о. логическая (булева) переменная – это такая величина Х, которая может применять только значения 0 или 1 т.е.
Считают, что высказывания = 1, если оно истинно и = 0, если ложно. Т.о. логическая (булева) переменная – это такая величина Х, которая может применять только значения 0 или 1 т.е. n=1 k=2n = 21 = 2 N=22 = 4 ФАЛ
n=1 k=2n = 21 = 2 N=22 = 4 ФАЛ Тождественная ФАЛ Fз (x)= x
Тождественная ФАЛ Fз (x)= x


 F10(X1,X2) = X1∞X2 = X1 = X2
F10(X1,X2) = X1∞X2 = X1 = X2
 F12 = (X1,X2)= X2 X1
F12 = (X1,X2)= X2 X1

 F14 (X1,X2) = X1 X2
F14 (X1,X2) = X1 X2
 1
1


 0
0







