
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Олимпиада по математике тусур, 2019. Курс задача 1 ⇐ ПредыдущаяСтр 3 из 3
Курс задача 1 Вычислить интеграл Решение. Сделаем замену
1-й элементарный, а во 2-м циклический интеграл. Рассмотрим
Вернёмся к сумме интегралов.
Ответ.
Примечание. Проверка.
Олимпиада по математике ТУСУР, 2019 Курс задача 2 Найти
Решение.
Здесь присутствует интегральная сумма функции В пределе эта интегральная сумма сходится к интегралу Ответ.
Олимпиада по математике ТУСУР, 2019 Курс задача 3 Найти общее решение дифференциального уравнения: Решение. Можно заметить, что правая часть - это производная от
Исследуем следующие производные от
Итак, уравнение сводится к Уравнение имеет вид Характеристическое: Общее решение
Олимпиада по математике ТУСУР, 2019 Курс задача 4 Найти сумму функционального ряда Решение. Заметим, что Запишем подробнее: Заметим, что при вычислении 2-й производной, в первой скобке получится точно такая же сумма, как и была, а во 2-й вместо степеней 1,5,9,... будут другие нечётные степени, которых не было ранее, а именно 3,7,...
Сумма исходной функции и её 2 производной содержит все степени,
Характкристическое уравнение Итак, общее решение неоднородного уравнения: Найдём константы. По строению ряда видно, что
Частное решение: Ответ.
Олимпиада по математике ТУСУР, 2019 Курс задача 5 Вычислить интеграл
Решение.
Далее оба интеграла решаются с помощью разложения рациональных дробей в сумму простейших.
Сравнивая числители, получаем
Тогда
Во втором интеграле (мнимая часть):
Ответ.
Олимпиада по математике ТУСУР, 2019 Курс задача 6 Три точки случайным образом брошены на отрезок [0,1]. Найти вероятность того, что произведение их абсцисс больше, чем
Решение.
На верхней грани выполнено
Ответ.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 70; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.186.92 (0.016 с.) |
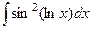 .
.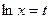 . Тогда
. Тогда  ,
, 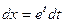 .
.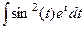 . По формуле понижения степени,
. По формуле понижения степени,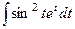 =
=  =
= 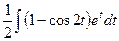 =
= 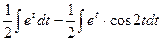
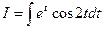 .
.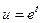
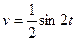

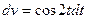
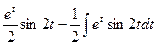 . Применив 2-е интегрирование по частям,
. Применив 2-е интегрирование по частям,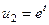
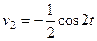
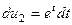

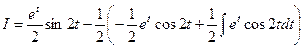

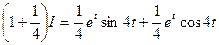

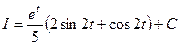 .
. =
=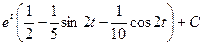 . После обратной замены:
. После обратной замены: 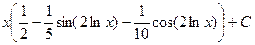 =
= .
.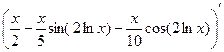 =
=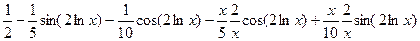 =
=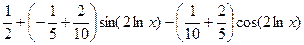 =
=  =
= 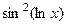 .
.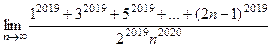 .
.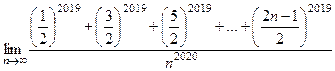 =
=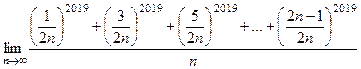
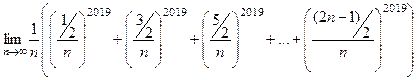
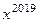 на отрезке [0,1], где значения функции рассматриваются ровно в серединах интервалов
на отрезке [0,1], где значения функции рассматриваются ровно в серединах интервалов 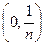 ,
, 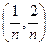 ,
, 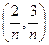 ,...
,...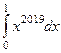 =
= 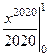 =
=  .
.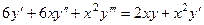
 :
: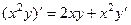
 =
= 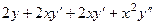 =
= 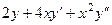 . Тогда 3-я производная:
. Тогда 3-я производная: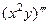
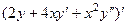 =
= 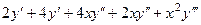 =
= 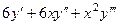 , что как раз и равно левой части.
, что как раз и равно левой части.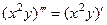 . Обозначим
. Обозначим 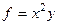 .
.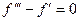 . Это линейное однородное уравнение.
. Это линейное однородное уравнение.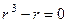 .
.  , корни 0, 1,
, корни 0, 1,  .
.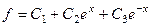 , то есть
, то есть 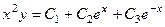 , тогда
, тогда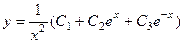 . Ответ.
. Ответ.  .
.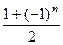 = 1 при чётном
= 1 при чётном  , и 0 при нечётном.
, и 0 при нечётном. =
= 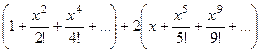 .
. .
.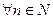 :
: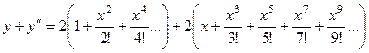 =
= 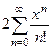 =
= 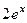 .
. - линейное неоднородное дифференциальное уравнение.
- линейное неоднородное дифференциальное уравнение.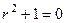 , корни
, корни 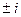 ,общее решение соответствующего однородного уравнения:
,общее решение соответствующего однородного уравнения: 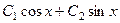 . По правой части
. По правой части 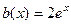 строим частное решение неоднородного уравнения. Число 1 не принадлежит множеству чисел
строим частное решение неоднородного уравнения. Число 1 не принадлежит множеству чисел  . Тогда
. Тогда 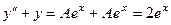 , откуда
, откуда 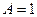 .
.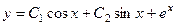 .
.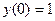 ,
,  .
.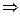
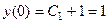
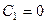

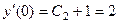
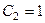
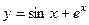 .
. 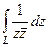 по неограниченной кривой
по неограниченной кривой 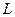 в комплексной плоскости, где
в комплексной плоскости, где 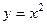 правее точки
правее точки  .
. 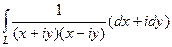 =
=  =
=  . При этом
. При этом 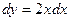 ,
,  .
. 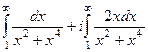 . Во втором подведём под знак дифференциала. При этом происходит замена
. Во втором подведём под знак дифференциала. При этом происходит замена 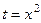 , и
, и 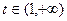
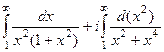 =
= 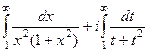 .
. =
= 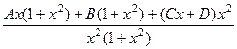 ,
,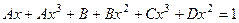
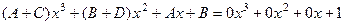 , откуда получаем 4 равенства:
, откуда получаем 4 равенства: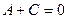 ,
, 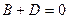 ,
,  ,
, 
 ,
, 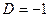 .
.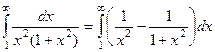 =
= 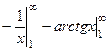 =
= 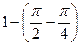 =
= 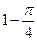 .
.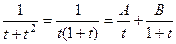 =
= 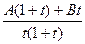 ,
, 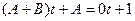
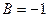 .
.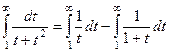 =
= 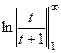 =
= 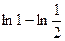 =
= 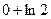 .
.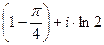 .
.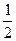 .
.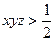 . Нужно найти отношение объёма тела, для точек которого выполняется
. Нужно найти отношение объёма тела, для точек которого выполняется  .
.

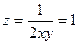
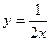 , это определяет границу проекции тела на горизонтальную плоскость, т.е. границы для двойного интеграла по
, это определяет границу проекции тела на горизонтальную плоскость, т.е. границы для двойного интеграла по  .
.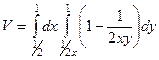 =
= 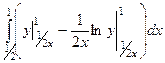 =
= 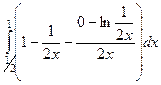 =
= 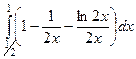 =
= 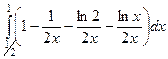 =
=  =
=  =
=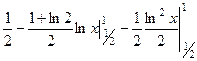 =
=  =
= 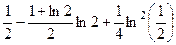 =
= 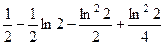 =
= 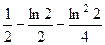 .
.


