
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема сложения вероятностей для НЕсовместных и совместных событий. Вероятность появления хотя бы одного события. Теоремы умножения для двух независимых и зависимых событий
Суммой А+В двух событий А и В называется событие, состоящее в появлении либо события А, либо события В, либо обоих этих событий вместе (рис.2.1). Теорема. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:
Теорема. Вероятность суммы нескольких попарно несовместных событий равна сумме вероятностей этих событий:
Следствие 1. Если события А1, А2, … А n образуют полную группу событий, то сумма их вероятностей равна 1:
Пример 2.5. В лотерее 1000 билетов, из них на один билет выпадает выигрыш 5000 рублей, на 10 билетов – выигрыш по 1000 рублей, на 50 билетов – выигрыши по 200 рублей, на 100 билетов – выигрыши по 50 рублей, остальные билеты невыигрышные. Некто покупает один билет. Найти вероятность выигрыша не менее 200 рублей. Решение: Рассмотрим события: А – выиграть не менее 200 руб., А1 – выиграть 200 руб., А2 – выиграть 1000 руб., А3 – выиграть 5000 руб. Очевидно, что А=А1+А2+А3 По теореме сложения вероятностей несовместных событий Р(А)=Р(А1)+Р(А2)+Р(А3)=0,05+0,01+0,001=0,061. Теорема. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Произведением двух событий А и В называется событие, состоящее в появлении и события А, и события В (рис.2.2). Пусть события А и В – зависимые события. Условной вероятностью РА(B) события В называется вероятность события В, найденная в предположении, что событие А уже наступило. Событие В называют независимым от события А, если появление события А не изменяет вероятности события В.
Теорема. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
В частности, для независимых событий:
т.е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий. Пример 2.6. Игральный кубик подбрасывают 2 раза. Какова вероятность того, что оба раза выпадет «шестерка»? Решение: Рассмотрим события: А – первый раз выпадет «шестерка» Пример 2.7. В цехе работают семь мужчин и три женщины. По табельным номерам наудачу отобраны три человека. Найти вероятность того, что все отобранные лица окажутся мужчинами.
Решение: Введем обозначение событий. А – первым отобран мужчина, В – вторым отобран мужчина, С – третьим отобран мужчина.
Теорема. Вероятность появления хотя бы одного из событий А1, А2,…, А n, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий
Пример 2.8. Три стрелка независимо друг от друга стреляют по цели. Вероятность попадания в цель первым стрелком равна 0,7; вторым – 0,8; третьим – 0,9. Найти вероятность того, что: a) все три стрелка попадут в цель; b) все три стрелка промахнутся; c) только один попадет; d) только два стрелка попадут в цель; e) не более двух стрелков попадут; f) хотя бы один стрелок попадет в цель. Решение: a) Пусть событие А – все три стрелка попадут в мишень. Обозначим вероятность того, что первый стрелок попадет в цель Р (1)=0,7; второй – Р (2)=0,8; третий – Р (3)=0,9. Тогда b) Обозначим вероятность того, что промахнется первый стрелок - Событие В – все три стрелка промахнулись. Тогда c) Пусть событие С состоит в том, что только один стрелок попадет в цель. Событие С произойдет, если произойдет либо событие А1:
d) Рассуждая аналогично предыдущему случаю, получим:
где D – событие, состоящее в том, что только два стрелка попадут в цель. e) Не более двух стрелков попадут в мишень, если произойдет либо событие B – все три стрелка промахнутся, либо событие С – только один стрелок попадет в мишень, либо событие D – только два стрелка попадут в мишень. Вероятности событий B, С, D известны: Р (B)=0,006, Р(С)= 0,092, Р(D)= 0,398. Следовательно, Р(E) = Р(В) + Р(С) + Р(Д) = 0,496, где E – событие, состоящее в том, что в результате опыта не более двух стрелков попадут в цель. f) Рассмотрим два события: F – хотя бы один стрелок попадет в мишень; событие B- все трое промахнутся. Эти события являются противоположными, следовательно:
Формула полной вероятности
Теорема. Если события Н1, Н2,… Нn образуют полную группу несовместных событий и событие А может наступить лишь при условии появления одного из событий Н i (i=1,2,…, n), то имеет место формула, которая называется формулой полной вероятности:
Входящие в формулу события Н1, Н2,… Нn называют гипотезами. Пример 2.9. В урну, содержащую два шара, опущен белый шар, после чего из неё наудачу извлечен один шар. Найти вероятность того, что извлеченный шар окажется белым, если одинаково возможны все предположения о первоначальном составе шаров (по цвету). Решение: Обозначим через А событие - извлечен белый шар. Возможны следующие предположения (гипотезы) о первоначальном составе шаров: В1 - белых шаров нет, В2 - один белый шар, В3 - два белых шара.
Поскольку всего имеется три гипотезы, причем по условию они равновероятны, и сумма вероятностей гипотез равна единице, то условная вероятность того, что будет извлечен белый шар, при условии, что первоначально в урне не было белых шаров, Условная вероятность того, что будет извлечен белый шар, при условии, что первоначально в урне был один белый шар, Условная вероятность того, что будет извлечен белый шар, при условии, что первоначально в урне было 2 белых шара, Искомую вероятность того, что будет извлечен белый шар, находим по формуле полной вероятности:
Формула Байеса Теорема. Пусть событие А может наступить лишь при условии появления одного из несовместных событий (гипотез) Н1, Н2,… Нn, которые образуют полную группу событий. Если событие А уже произошло, то вероятности гипотез могут быть переоценены по формуле Байеса
Пример 2.10. В группе из 10 студентов, пришедших на экзамен, 3 подготовлены отлично, 4 – хорошо, 2 – удовлетворительно и 1 – плохо. Имеется 20 вопросов, причем: отлично подготовленный студент может ответить на все вопросы, хорошо подготовленный – на 16, удовлетворительно подготовленный – на 10 и плохо подготовленный – на 5. Найти вероятность того, что случайно выбранный студент сможет ответить на доставшийся ему вопрос, и вероятность того, что этот студент плохо подготовлен и ему просто повезло с вопросом. Решение: Введем следующие обозначения для заданных величин: Н1 – студент отличник Н2 – студент учится хорошо Н3 - студент учится удовлетворительно Н4 – студент учится плохо А – вопрос “хороший” P (H 1)= 0,3 (3 из 10) P (Н2) =0,4 (4 из 10) P (Н3) =0,2 (2 из 10) P (Н4) =0,1 (1 из 10) P (A / H 1) =20/20=1 P (А/Н2) = 16/20=0,8 P (А/Н3)= 10/20=0,5 P (А/Н4)= 5/20=0,25 Воспользуемся формулой полной вероятности для вычисления P (А): и формулой Байеса для вычисления P (Н4/А):
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 142; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.153.69 (0.02 с.) |

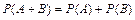
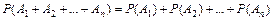
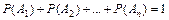


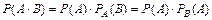
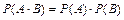
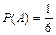 и В – второй раз выпадет «шестерка»
и В – второй раз выпадет «шестерка» 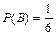 . События А и В независимы. Тогда
. События А и В независимы. Тогда 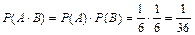
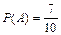
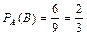
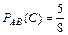
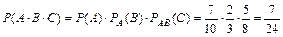
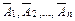 :
: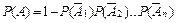
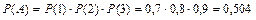 .
.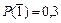 ; промахнется второй –
; промахнется второй – 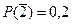 ; промахнется третий –
; промахнется третий – 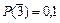 .
. .
.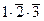 , либо событие А2:
, либо событие А2: 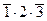 , либо событие А3:
, либо событие А3: 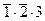 . Переходя к вероятностям, получим:
. Переходя к вероятностям, получим: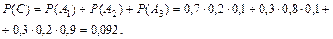
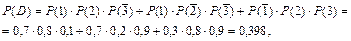
 .
.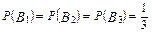
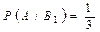
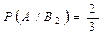 .
.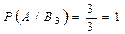 .
.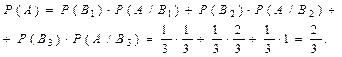 .
.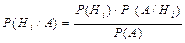 , (i =1,2,… n),
где Р(А) =Р(Н1) Р(А/ Н1)+…+ Р(Н n) Р(А/ Н n).
, (i =1,2,… n),
где Р(А) =Р(Н1) Р(А/ Н1)+…+ Р(Н n) Р(А/ Н n).
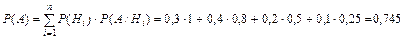
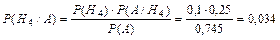 .
.


