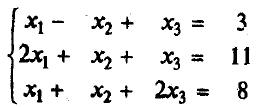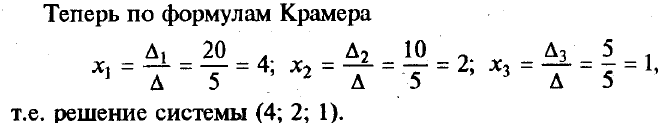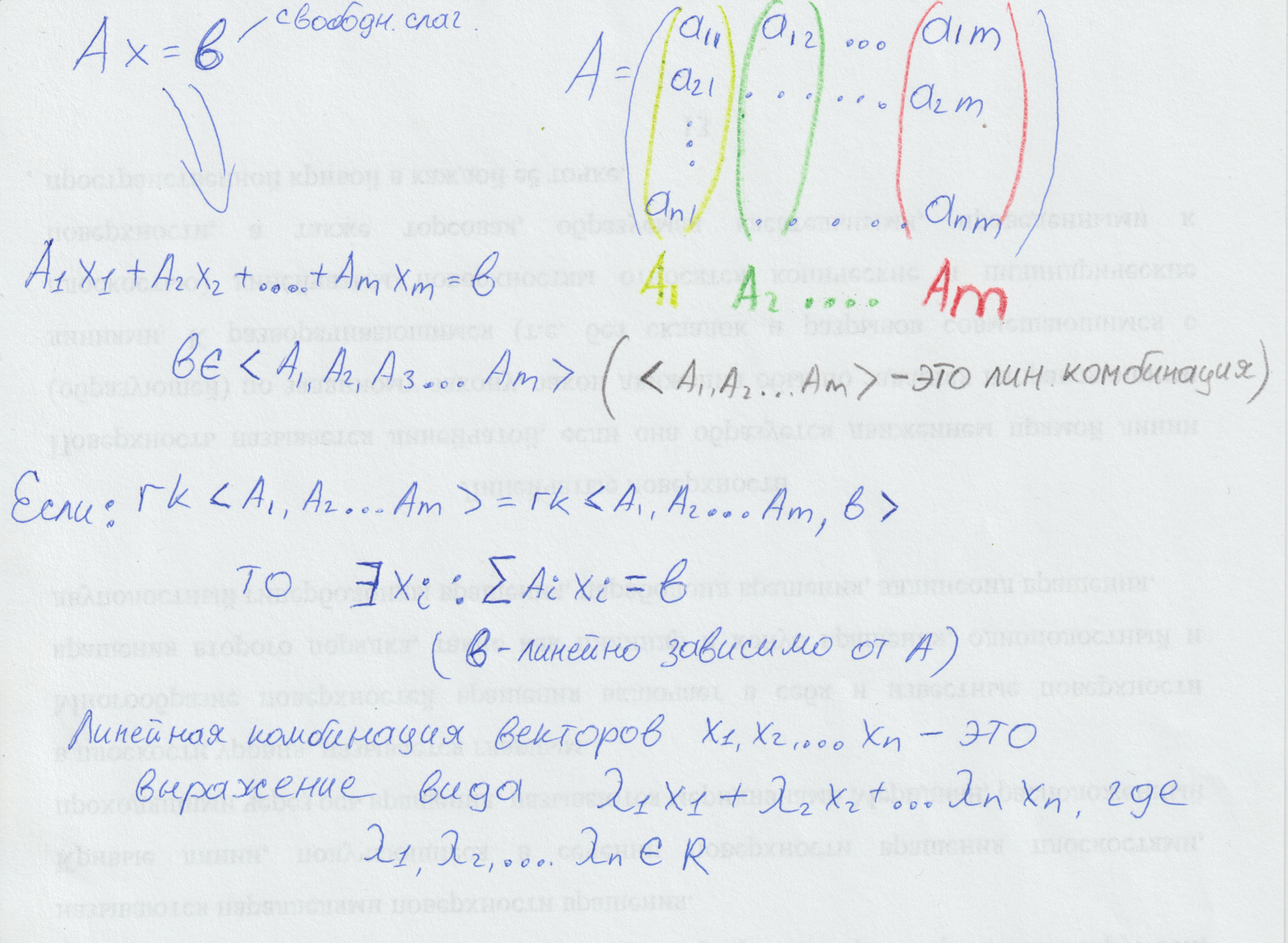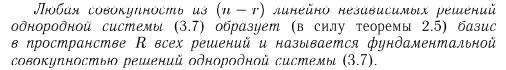Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод решения систем линейных уравнений с квадратной матрицей по формулам Крамера
Пусть n = 2:
Если обе части первого уравнения умножить на a22, а обе части второго – на (-a12), и затем сложить полученные уравнения, то мы исключим из системы переменную x2. Аналогично можно исключить переменную x1 (умножив обе части первого уравнения на (-a21), а обе части второго – на a11). В результате получим систему:
Выражение в скобках есть определитель системы
Обозначим
Тогда система примет вид:
Из полученной системы следует, что если определитель системы
Теорема Крамера (доказательство опустим). Если определитель матрицы системы n уравнений D не равен нулю, то система имеет единственное решение, определяемое по формулам:
где Dj - определитель матрицы, получаемой из матрицы А заменой j-го столбца столбцом свободных членов. В качестве примера решим этим методом систему, которую до этого решали методом обратной матрицы:
Недостатки рассмотренных методов: 1) существенная трудоемкость (вычисление определителей и нахождение обратной матрицы); 2) ограниченная область применения (для систем с квадратной матрицей).
Метод Гаусса (метод последовательного исключения переменных) Этот метод используется для решения системы m линейных уравнений с n переменными в общем виде. Его суть заключается в применении к расширенной матрице системы равносильных преобразований, с помощью которых система уравнений преобразуется к виду, когда ее решения становится легко найти (если они есть). Это такой вид, в котором левая верхняя часть матрицы системы будет представлять собой ступенчатую матрицу. Этого добиваются с помощью тех же приемов, с помощью которых получали ступенчатую матрицу с целью определения ранга. При этом применяют к расширенной матрице элементарные преобразования, которые позволят получить равносильную систему уравнений. После этого расширенная матрица примет вид:
Билет 5. Линейные (векторные) пространства. Линейная зависимость и независимость векторов. Базис и размерность линейного пространства. Координаты вектора в заданном базисе. Множество L называется линейным или векторным пространством, если для всех элементов (векторов) этого множества определены операции сложения и умножения на число и справедливо:
1. Каждой паре элементов x и y из L отвечает элемент x + y из L, называемый суммой x и y, причём: Аксиом 1)x + y = y + x − сложение коммутативно;
2)x + (y + z) = (x + y) + z − сложение ассоциативно;
3)x + 0 = x − существует единственный нулевой элемент 0 (x + 0 = x для любого x из L);
4)x + (− x) = 0 − для каждого элемента x из L существует единственный противоположный элемент −x (x + (−x) = 0 для любого x из L).
Каждой паре x и α, где α − число, а x элемент из L, отвечает элемент α·x, называемый произведением α и x, причём:
5)α·(β·x) = (α·β)·x − умножение на число ассоциативно:;
6)1·x = x − для любого элемента x из L.
7)α·(x + y) = α·x + α·y − умножение на число дистрибутивно относительно сложения элементов;
8)(α + β)·x = α·x + β·x − умножение на вектор дистрибутивно относительно сложения чисел. Следствие аксиом: В линейном пространстве определена операция вычитания.
Система векторов x,y,z называется линейной зависимой, если найдутся такие числа A,S,D, не все =0 одновременно, что выполняется равенство; Ax+Sy+Dz=0 Также система линейно зависима, если одни из векторов является линейной комбинацией остальных. Линейно не зависима, если A,S,D=0
Пусть X — линейное пространство.
Определение: Если существует натуральное число n такое, что X содержит линейно независимую систему из n векторов, а любая система из n + 1 вектора линейно зависима, то X называется n –мерным линейным пространством, а число n – его размерностью.
Будем обозначать n –мерное линейное пространство Xn, где n = dimXn — размерность пространства Xn.
Из определения следует, что размерность линейного пространства равна максимальному количеству линейно независимых векторов.
Замечания.
1. Размерность пространства, состоящего только из одного нулевого вектора, равна нулю. Такое пространство называется тривиальным. 2. Если в линейном пространстве существует любое число линейно независимых векторов, то такое пространство называется бесконечномерным.
Определение. Упорядоченная система векторов e1, e2, …, en ∈ X называется базисом в X, если
1. система векторов e1, e2, …, en линейно независима; 2. любой вектор x пространства X может быть представлен в виде(то есть разложить по базису) x = ξ1e1 + ξ2e2 + … + ξnen. (1)
Выражение (1) называется разложением вектора x по базису e1, e2, …, en.
Коэффициенты ξ1, ξ2, …, ξn в разложении вектора по данному базису определяются однозначно.
Коэффициенты разложения (1) вектора x по базису e1, e2, …, en называются координатами вектора x в этом базисе.
Удобно использовать обозначение для i –ой координаты ξi = бei, xс и для вектора x = {ξ1, ξ2, …, ξn}. Координаты вектора записывают также в виде матрицы–столбца
ξ1 ξ2 … ξn
который называется координатным столбцом вектора x.
В n–мерном линейном пространстве Xn существует базис. Он содержит n векторов.
Замечания.
1. В линейном пространстве существует бесчисленное множество базисов.
2. В бесконечномерном пространстве всегда существует базис. Он содержит бесконечное множество векторов
3. Любая упорядоченная линейно независимая система из n векторов в n–мерном пространстве является базисом.
Свойства базиса 1)Координаты вектора в базисе определяются однозначно. 2)При сложении двух векторов их координаты складываются 3)Если система содержит систему единичных векторов, то они образуют базис этой системы.
Билет 6. Ранг матрицы. Сохранение ранга матрицы при элементарных преобразованиях строк и столбцов матрицы. Методы вычисления ранга матрицы. Ранг матрицы — наивысший из порядков всевозможных ненулевых миноров этой матрицы. Ранг нулевой матрицы любого размера - ноль. Если все миноры второго порядка равны нулю, то ранг равен единице, и т.д. Ранг матрицы — размерность образа линейного оператора, которому соответствует матрица. Минор, который определяет ранг матрицы называется базисным минором. Следствие 1. Ранг матрицы А совпадает с количеством линейно независимых строк(столбцов) матрицы А.
Элементарные преобразования не изменяют ранг матрицы.
· Перестановка строк или столбцов матрицы изменяет только знак определителя. · При умножении строки (столбца) матрицы на ненулевое число определитель умножается на это число. · Определитель не изменяется, если к строке (столбцу) прибавляется другая строка (столбец).
Методы вычисления ранга матрицы
1. Метод окаймляющих миноров. Ранг матрицы будет равен наивысшему порядку минора, отличного от нуля.
2. Приведение матрицы к диагональному виду путем элементарных преобразований. Ранг матрицы будет равен количеству ненулевых диагональных элементов. Билет 7. Совместность систем линейных уравнений. Теорема Кронекера–Капелли. Структура общего решения однородной системы линейных уравнений. Фундаментальная система решений. Нахождение общего решения неоднородной системы линейных уравнений. Линейные операторы в линейном пространстве. Матрица линейного оператора. Совместность систем линейных уравнений означает, что вектор свободных слагаемых является линейной комбинацией столбцов матрицы.
Теорема Кронекера-Копелли – система линейных алгебраических уравнений совместна тогда, и только тогда, когда ранг ее матрицы равен рангу расширенной матрицы (A|b – расширенная матрица) *Если r<n è ОО множество решений
Фундаментальная система решений – всякий базис пространства решений.
Нахождение решения неоднородной системы уравнений происходит по полной аналогии с нахождением решений для однородной системы
* y =образ, x =прообраз
|
|||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 254; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.25.32 (0.025 с.) |

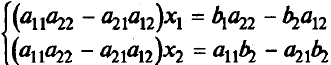
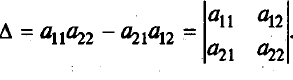
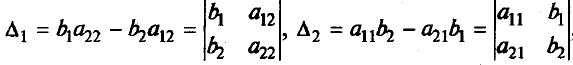
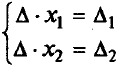
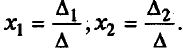
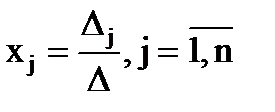 , формула Крамера.
, формула Крамера.