Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определители. Свойства определителя. Методы вычисления определителей второго, третьего и n -ого порядка. Миноры и алгебраические дополнения, разложение определителя по строке или по столбцу.Стр 1 из 6Следующая ⇒
Билет №1 Определение матрицы. Линейные операции с матрицами. Умножение матриц. Транспонирование матриц. Блочные матрицы. Элементарные преобразования матриц. Матрица размера m х n – это прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы. Например, рассмотрим матрицу А размерности 2 х 3:
В этой матрице две строки (m = 2) и три столбца (n = 3), т.е. она состоит из шести элементов aij, где i - номер строки, j - номер столбца. При этом принимает значения от 1 до 2, а от одного до трех (записывается
Матрицы А и В одного размера (m х n) называют равными, если они поэлементно совпадают, т.е. aij = bij для
Матрица-строка – это матрица, состоящая из одной строки, а матрица-столбец – это матрица, состоящая из одного столбца. Например, Квадратная матрица n-го порядка – это матрица, в число строк равно числу столбцов и равно n. Например, Диагональные элементы матрицы – это элементы, у которых номер строки равен номеру столбца (aij, i = j). Эти элементы образуют главную диагональ матрицы. В предыдущем примере главную диагональ образуют элементы a11= 3 и a22= 5. Диагональная матрица – это квадратная матрица, в которой все недиагональные элементы равны нулю. Например, Матрица называется нулевой, если все ее элементы равны нулю. Квадратная матрица называется треугольной, если все ее элементы ниже (или выше) главной диагонали равны нулю. Например, Операции над матрицами Над матрицами можно производить следующие операции:
1. Умножение матрицы на число. Произведением матрицы А на число l называется матрица В = lА, элементы которой bij = laij для любых i и j. Например, если
2. Сложение матриц. Суммой двух матриц А и В одинакового размера m х n называется матрица С = А + В, элементы которой сij = aij + bij для "i, j.
Отметим, что через предыдущие операции можно определить вычитание матриц одинакового размера: разность А-В = А + (-1)*В.
3. Умножение матриц. Произведением матрицы А размера m x n на матрицу В размера n x p называется такая матрица С, каждый элемент которой сij равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В, т.е. Например, если
В этом случае матрица А называется согласованной с матрицей В.
Для нахождения суммы или разности матриц их размер обязательно должен быть одинаковым. Для нахождения произведения матриц число столбцов первой из них должно совпадать с числом строк второй (такие матрицы называют согласованными).
Рассмотрим некоторые свойства рассмотренных операций, аналогичные свойствам операций над числами. 1) Коммутативный (переместительный) закон сложения: А + В = В + А 2) Ассоциативный (сочетательный) закон сложения: (А + В) + С = А + (В + С) 3) Дистрибутивный (распределительный) закон умножения относительно сложения: l(А + В) = lА + lВ А (В + С) = АВ + АС (А + В) С = АС + ВС 5) Ассоциативный (сочетательный) закон умножения: l(АВ) = (lА)В = А(lВ) A(BС) = (АВ)С AB ¹ BA. АЕ = ЕА = А В самом деле,
Подчеркнем еще одно отличие умножения матриц от умножения чисел. Произведение чисел может равняться нулю тогда и только тогда, когда хотя бы одно из них равно нулю. О матрицах этого сказать нельзя, т.е. произведение ненулевых матриц может равняться нулевой матрице. Например,
Продолжим рассмотрение операций над матрицами.
Свойства операции транспонирования: 1) Из определения следует, что если матрицу транспонировать дважды, мы вернемся к исходной матрице: (AT)T = A. 2) Постоянный множитель можно вынести за знак транспонирования: (lА)T = lАT.
3) Транспонирование дистрибутивно относительно умножения и сложения матриц: (AB)T = BTAT и (A + B)T = BT + AT.
Например:
Элементарные преобразования матриц: · Перестановка местами двух параллельных рядов матрицы · Умножение всех элементов ряда матрица на число, отличное от нуля · Прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число. Билет №2 Метод обратной матрицы Рассмотрим в общем виде систему уравнений АХ = В с невырожденной квадратной матрицей А. В этом случае существует обратная матрица А-1. Домножим слева обе части на А-1. Получим А-1АХ = А-1В. Отсюда ЕХ = А-1В и Х = А-1В. Последнее равенство представляет собой матричную формулу для нахождения решения таких систем уравнений. Использование этой формулы получило название метода обратной матрицы
Например, решим этим методом следующую систему:
В конце решения системы можно сделать проверку, подставив найденные значения в уравнения системы. При этом они должны обратиться в верные равенства. Для рассмотренного примера проведем проверку:
Аксиом 1)x + y = y + x − сложение коммутативно;
2)x + (y + z) = (x + y) + z − сложение ассоциативно;
3)x + 0 = x − существует единственный нулевой элемент 0 (x + 0 = x для любого x из L);
4)x + (− x) = 0 − для каждого элемента x из L существует единственный противоположный элемент −x (x + (−x) = 0 для любого x из L).
Каждой паре x и α, где α − число, а x элемент из L, отвечает элемент α·x, называемый произведением α и x, причём:
5)α·(β·x) = (α·β)·x − умножение на число ассоциативно:;
6)1·x = x − для любого элемента x из L.
7)α·(x + y) = α·x + α·y − умножение на число дистрибутивно относительно сложения элементов;
8)(α + β)·x = α·x + β·x − умножение на вектор дистрибутивно относительно сложения чисел. Следствие аксиом: В линейном пространстве определена операция вычитания.
Система векторов x,y,z называется линейной зависимой, если найдутся такие числа A,S,D, не все =0 одновременно, что выполняется равенство; Ax+Sy+Dz=0 Также система линейно зависима, если одни из векторов является линейной комбинацией остальных. Линейно не зависима, если A,S,D=0
Пусть X — линейное пространство.
Определение: Если существует натуральное число n такое, что X содержит линейно независимую систему из n векторов, а любая система из n + 1 вектора линейно зависима, то X называется n –мерным линейным пространством, а число n – его размерностью.
Будем обозначать n –мерное линейное пространство Xn, где n = dimXn — размерность пространства Xn.
Из определения следует, что размерность линейного пространства равна максимальному количеству линейно независимых векторов.
Замечания.
1. Размерность пространства, состоящего только из одного нулевого вектора, равна нулю. Такое пространство называется тривиальным. 2. Если в линейном пространстве существует любое число линейно независимых векторов, то такое пространство называется бесконечномерным.
Определение. Упорядоченная система векторов e1, e2, …, en ∈ X называется базисом в X, если
1. система векторов e1, e2, …, en линейно независима; 2. любой вектор x пространства X может быть представлен в виде(то есть разложить по базису) x = ξ1e1 + ξ2e2 + … + ξnen. (1)
Выражение (1) называется разложением вектора x по базису e1, e2, …, en.
Коэффициенты ξ1, ξ2, …, ξn в разложении вектора по данному базису определяются однозначно.
Коэффициенты разложения (1) вектора x по базису e1, e2, …, en называются координатами вектора x в этом базисе.
Удобно использовать обозначение для i –ой координаты ξi = бei, xс и для вектора x = {ξ1, ξ2, …, ξn}. Координаты вектора записывают также в виде матрицы–столбца
ξ1 ξ2 … ξn
который называется координатным столбцом вектора x.
В n–мерном линейном пространстве Xn существует базис. Он содержит n векторов.
Замечания.
1. В линейном пространстве существует бесчисленное множество базисов.
2. В бесконечномерном пространстве всегда существует базис. Он содержит бесконечное множество векторов
3. Любая упорядоченная линейно независимая система из n векторов в n–мерном пространстве является базисом.
Свойства базиса 1)Координаты вектора в базисе определяются однозначно. 2)При сложении двух векторов их координаты складываются 3)Если система содержит систему единичных векторов, то они образуют базис этой системы.
Билет 6. Ранг матрицы. Сохранение ранга матрицы при элементарных преобразованиях строк и столбцов матрицы. Методы вычисления ранга матрицы. Ранг матрицы — наивысший из порядков всевозможных ненулевых миноров этой матрицы. Ранг нулевой матрицы любого размера - ноль. Если все миноры второго порядка равны нулю, то ранг равен единице, и т.д. Ранг матрицы — размерность образа линейного оператора, которому соответствует матрица. Минор, который определяет ранг матрицы называется базисным минором. Следствие 1. Ранг матрицы А совпадает с количеством линейно независимых строк(столбцов) матрицы А.
Элементарные преобразования не изменяют ранг матрицы.
· Перестановка строк или столбцов матрицы изменяет только знак определителя. · При умножении строки (столбца) матрицы на ненулевое число определитель умножается на это число. · Определитель не изменяется, если к строке (столбцу) прибавляется другая строка (столбец).
Методы вычисления ранга матрицы
1. Метод окаймляющих миноров. Ранг матрицы будет равен наивысшему порядку минора, отличного от нуля.
2. Приведение матрицы к диагональному виду путем элементарных преобразований. Ранг матрицы будет равен количеству ненулевых диагональных элементов. Билет 7. Совместность систем линейных уравнений. Теорема Кронекера–Капелли. Структура общего решения однородной системы линейных уравнений. Фундаментальная система решений. Нахождение общего решения неоднородной системы линейных уравнений. Линейные операторы в линейном пространстве. Матрица линейного оператора. Совместность систем линейных уравнений означает, что вектор свободных слагаемых является линейной комбинацией столбцов матрицы.
Теорема Кронекера-Копелли – система линейных алгебраических уравнений совместна тогда, и только тогда, когда ранг ее матрицы равен рангу расширенной матрицы (A|b – расширенная матрица) *Если r<n è ОО множество решений
Фундаментальная система решений – всякий базис пространства решений.
Нахождение решения неоднородной системы уравнений происходит по полной аналогии с нахождением решений для однородной системы
* y =образ, x =прообраз
Совпадать Если их соответствующие коэффициенты пропорциональны, то есть, существует такое число «лямбда», что выполняются равенства: A 1 / A 2 = B 1 / B 2 = C 1 / C 2 = v 2) быть п а раллельными: Если их коэффициенты при переменных 3) пересекаться в единственной точке: Угол между двумя прямыми В геометрии за угол между двумя прямыми принимается МЕНЬШИЙ угол, из чего автоматически следует, что он не может быть тупым Рассмотрим две прямые, заданные уравнениями в общем виде: · Если прямые не перпендикулярны, то ориентированный угол
Расстояние от точки до прямой – это длина перпендикулярного отрезка, соединяющего данную точку и точку лежащую на прямой. Расстояние
Найти расстояние от точки Решение: всё что нужно, это аккуратно подставить числа в формулу и провести вычисления: Ответ: Билет№16. Прямая в пространстве и ее уравнение. Общие уравнения прямой в пространстве, приведение к каноническому виду. Взаимное расположение двух прямых, прямой и плоскости в пространстве. Угол между прямой и плоскостью, между двумя прямыми.
Билет№18 http://kvm.gubkin.ru/pub/vnz/Pismennyi.pdf Ответы на билет страница 91 Билет №1 Определение матрицы. Линейные операции с матрицами. Умножение матриц. Транспонирование матриц. Блочные матрицы. Элементарные преобразования матриц.
Матрица размера m х n – это прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы. Например, рассмотрим матрицу А размерности 2 х 3:
В этой матрице две строки (m = 2) и три столбца (n = 3), т.е. она состоит из шести элементов aij, где i - номер строки, j - номер столбца. При этом принимает значения от 1 до 2, а от одного до трех (записывается
Матрицы А и В одного размера (m х n) называют равными, если они поэлементно совпадают, т.е. aij = bij для
Матрица-строка – это матрица, состоящая из одной строки, а матрица-столбец – это матрица, состоящая из одного столбца. Например, Квадратная матрица n-го порядка – это матрица, в число строк равно числу столбцов и равно n. Например, Диагональные элементы матрицы – это элементы, у которых номер строки равен номеру столбца (aij, i = j). Эти элементы образуют главную диагональ матрицы. В предыдущем примере главную диагональ образуют элементы a11= 3 и a22= 5. Диагональная матрица – это квадратная матрица, в которой все недиагональные элементы равны нулю. Например, Матрица называется нулевой, если все ее элементы равны нулю. Квадратная матрица называется треугольной, если все ее элементы ниже (или выше) главной диагонали равны нулю. Например, Операции над матрицами Над матрицами можно производить следующие операции:
1. Умножение матрицы на число. Произведением матрицы А на число l называется матрица В = lА, элементы которой bij = laij для любых i и j. Например, если
2. Сложение матриц. Суммой двух матриц А и В одинакового размера m х n называется матрица С = А + В, элементы которой сij = aij + bij для "i, j.
Отметим, что через предыдущие операции можно определить вычитание матриц одинакового размера: разность А-В = А + (-1)*В.
3. Умножение матриц. Произведением матрицы А размера m x n на матрицу В размера n x p называется такая матрица С, каждый элемент которой сij равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В, т.е. Например, если
В этом случае матрица А называется согласованной с матрицей В.
Для нахождения суммы или разности матриц их размер обязательно должен быть одинаковым. Для нахождения произведения матриц число столбцов первой из них должно совпадать с числом строк второй (такие матрицы называют согласованными).
Рассмотрим некоторые свойства рассмотренных операций, аналогичные свойствам операций над числами. 1) Коммутативный (переместительный) закон сложения: А + В = В + А 2) Ассоциативный (сочетательный) закон сложения: (А + В) + С = А + (В + С) 3) Дистрибутивный (распределительный) закон умножения относительно сложения: l(А + В) = lА + lВ А (В + С) = АВ + АС (А + В) С = АС + ВС 5) Ассоциативный (сочетательный) закон умножения: l(АВ) = (lА)В = А(lВ) A(BС) = (АВ)С AB ¹ BA. АЕ = ЕА = А В самом деле,
Подчеркнем еще одно отличие умножения матриц от умножения чисел. Произведение чисел может равняться нулю тогда и только тогда, когда хотя бы одно из них равно нулю. О матрицах этого сказать нельзя, т.е. произведение ненулевых матриц может равняться нулевой матрице. Например,
Продолжим рассмотрение операций над матрицами.
Свойства операции транспонирования: 1) Из определения следует, что если матрицу транспонировать дважды, мы вернемся к исходной матрице: (AT)T = A. 2) Постоянный множитель можно вынести за знак транспонирования: (lА)T = lАT. 3) Транспонирование дистрибутивно относительно умножения и сложения матриц: (AB)T = BTAT и (A + B)T = BT + AT.
Например:
Элементарные преобразования матриц: · Перестановка местами двух параллельных рядов матрицы · Умножение всех элементов ряда матрица на число, отличное от нуля · Прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число. Билет №2 Определители. Свойства определителя. Методы вычисления определителей второго, третьего и n -ого порядка. Миноры и алгебраические дополнения, разложение определителя по строке или по столбцу. Определители матриц порядка N называется алгебраическая сумма n! Членов составленная следующим образом: члены определителя служат все возможные элементы матрицы взятые по одному из каждой строки и из каждой столбца, причем слагаемое берется со знаком плюс, если множество вторых индексов является четной перестановки.
Для матрицы А первого порядка ее определителем называют ее единственный элемент |А| = D1 = а11.
Для матрицы А второго порядка ее определителем называют число, которое вычисляют по формуле |А| = D2 = а11* а22 – а21* а12
Для матрицы А третьего порядка ее определителем называют число, которое вычисляют по формуле
Оно представляет алгебраическую сумму, состоящую из 6 слагаемых, в каждое из которых входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Для запоминания формулы определителя принято пользоваться так называемым правилом треугольников или правилом Сарруса (рисунок 6.1).
Определители более высоких порядков вычисляют рекуррентным способом, т.е. определитель четвертого порядка через определитель третьего порядка, определитель пятого порядка через определитель четвертого порядка и т.д. Минором Мij элемента аij матрицы n-го порядка называют определитель матрицы (n-1)-го порядка, полученной из матрицы А вычеркиванием i-й строки и j-го столбца.
Каждая матрица n-го порядка имеет n2 миноров (n-1)-го порядка.
Алгебраическим дополнением Aij элемента аij матрицы n-го порядка называют его минор, взятый со знаком (-1)(i+j): Aij = (-1)(i+j)*Мij Из определения следует, что Aij = Мij, если сумма номеров строки и столбца четная, и Aij = -Мij, если она нечетная. Например, если
Способ вычисления определителя состоит в следующем: определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
Основные свойства определителей.
1.Если какая-либо строка или столбец матрицы состоит из одних нулей, то определитель равен 0 (следует из способа расчета).
2.Если все элементы какой-либо строки (столбца) матрицы умножить на одно и то же число, то и ее определитель умножится на это число (также следует из способа расчета – на расчет алгебраических дополнений общий множитель не влияет, а все остальные слагаемые умножены именно на это число). Например,
3. При транспонировании матрицы ее определитель не изменяется: |АТ| = |А| (доказательство проводить не будем).
4. При перестановке местами двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.
5. Если матрица содержит две одинаковые строки (столбца), то ее определитель равен 0. В самом деле, если одинаковые строки (столбцы) переставить местами, то будет получена та же самая матрица с тем же самым определителей. С другой стороны, по предыдущему свойству он должен поменять знак, т.е. D = -D Û D = 0.
6. Если элементы двух строк (столбцов) матрицы пропорциональны, то определитель равен 0. 7. Сумма произведений элементов любой строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) той же матрицы всегда равна 0:
8. Определитель матрицы не изменяется, если к элементам строки или столбца матрицы прибавить элементы другой строки (столбца), умноженные на одно и тоже число.
9. Определитель произведения матриц равен произведению их определителей: |АВ| = |А| * |В|.
|
||||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 351; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.23.30 (0.268 с.) |
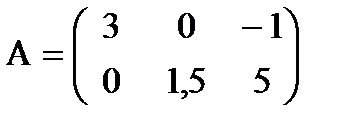
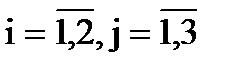 ). А именно, a11= 3; a12= 0; a13= -1; a21= 0; a22= 1,5; a23= 5.
). А именно, a11= 3; a12= 0; a13= -1; a21= 0; a22= 1,5; a23= 5.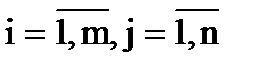 , т.е. для любых i и j (можно записать "i, j).
, т.е. для любых i и j (можно записать "i, j).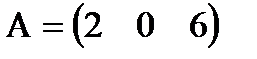 - матрица-строка, а
- матрица-строка, а 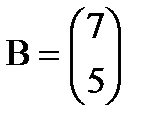 .
.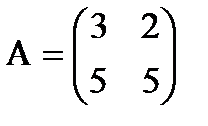 - квадратная матрица второго порядка.
- квадратная матрица второго порядка.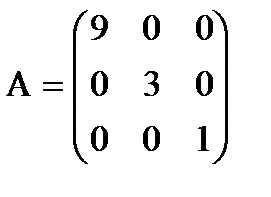 - диагональная матрица третьего порядка. Если при этом все диагональные элементы равны единице, то матрица называется единичной (обычно обозначаются буквой Е). Например,
- диагональная матрица третьего порядка. Если при этом все диагональные элементы равны единице, то матрица называется единичной (обычно обозначаются буквой Е). Например, 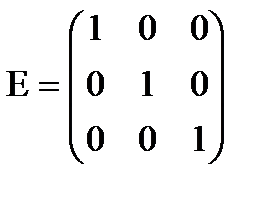 - единичная матрица третьего порядка.
- единичная матрица третьего порядка. - треугольная матрица третьего порядка.
- треугольная матрица третьего порядка.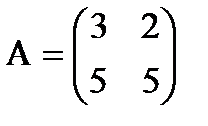 , то
, то 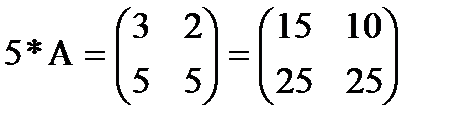 .
.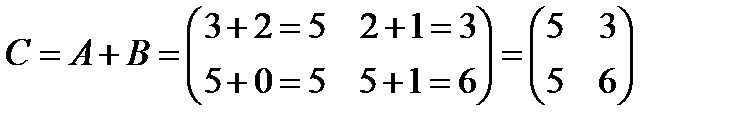 Например, если
Например, если 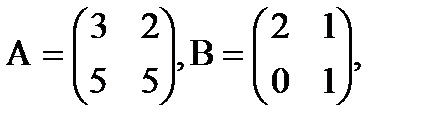 то
то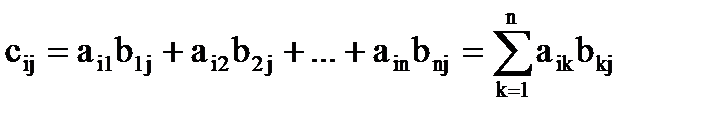 .
.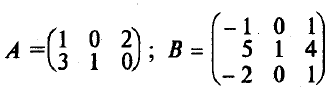 , то размер матрицы-произведения будет 2 x 3, и она будет иметь вид:
, то размер матрицы-произведения будет 2 x 3, и она будет иметь вид: 
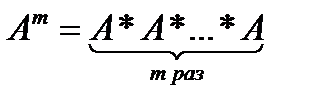 На основе операции умножения для квадратных матриц определена операция возведения в степень. Целой положительной степенью Аm (m > 1) квадратной матрицы А называются произведение m матриц, равных А, т.е.
На основе операции умножения для квадратных матриц определена операция возведения в степень. Целой положительной степенью Аm (m > 1) квадратной матрицы А называются произведение m матриц, равных А, т.е.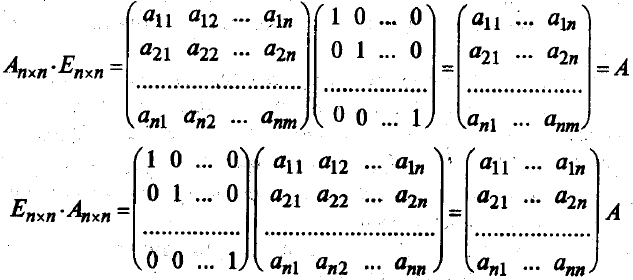
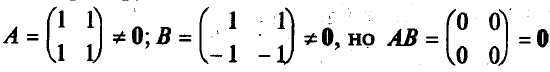
 4. Транспонирование матрицы представляет собой операцию перехода от матрицы А размера m x n к матрице АТ размера n x m, в которой строки и столбцы поменялись местами:
4. Транспонирование матрицы представляет собой операцию перехода от матрицы А размера m x n к матрице АТ размера n x m, в которой строки и столбцы поменялись местами: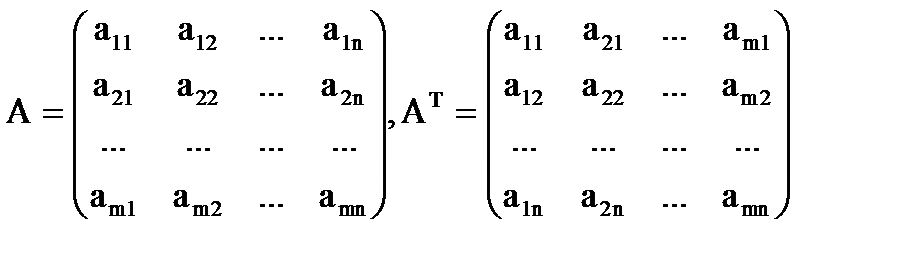 .
.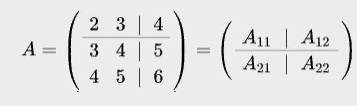 Блочные матрицы- числовая матрица разделенная на блоки каждый из которых являются матрицей.
Блочные матрицы- числовая матрица разделенная на блоки каждый из которых являются матрицей.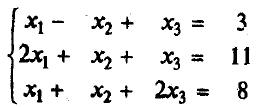
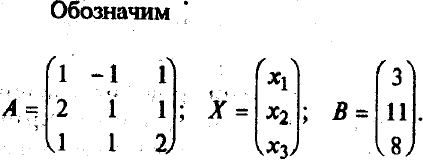

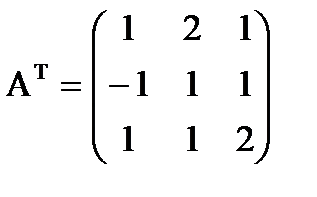 ;
; 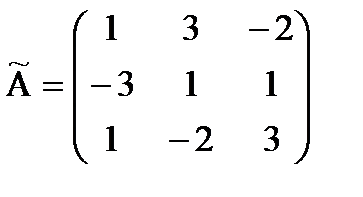
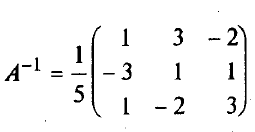
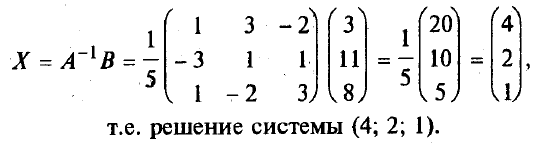
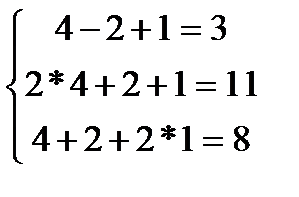



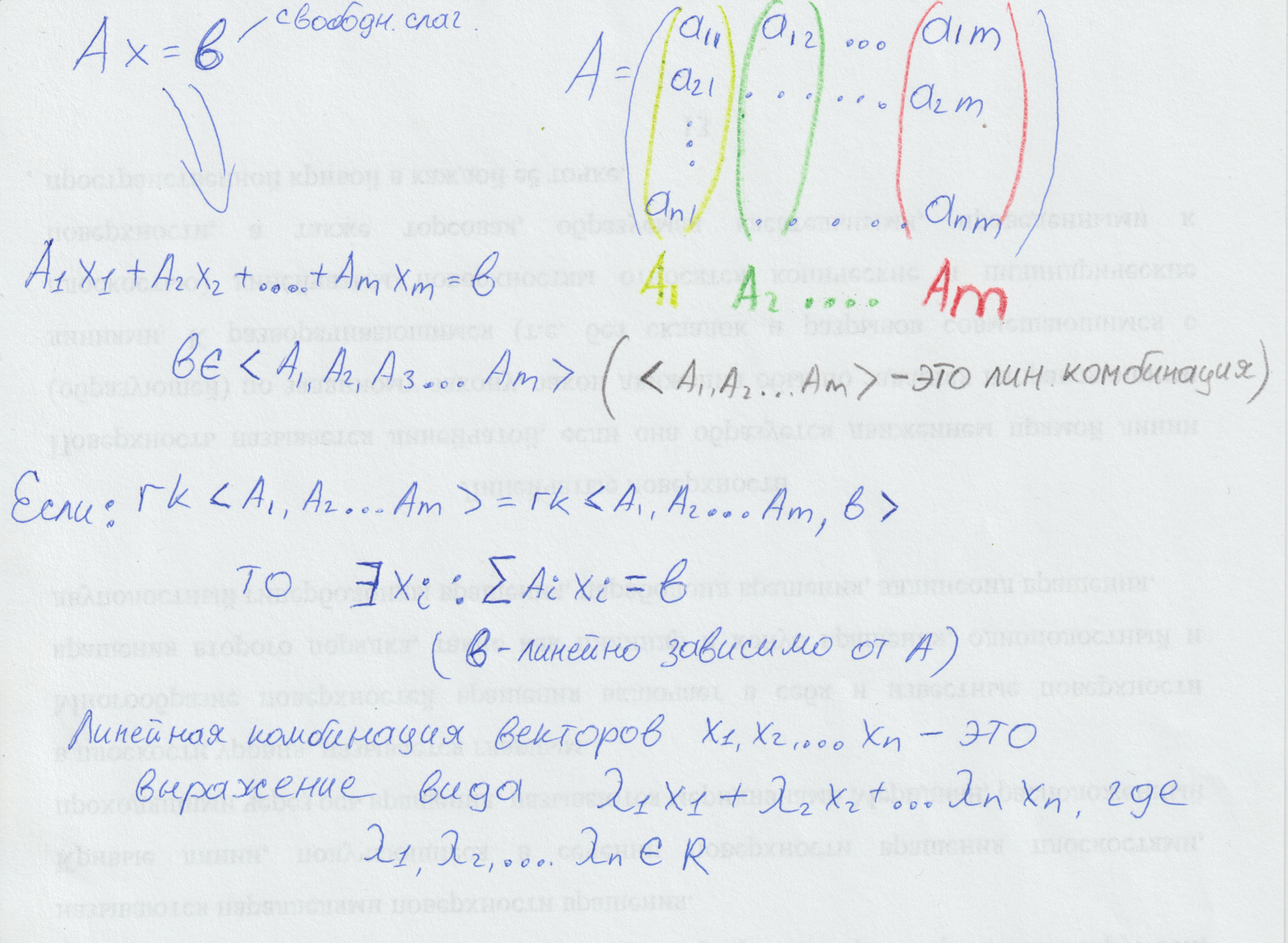

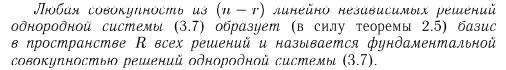







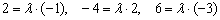
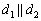 ;
;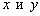 пропорциональны:
пропорциональны: 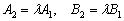 , но
, но 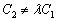 .
.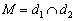 .
.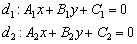
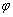 между ними можно вычислить с помощью формулы:
между ними можно вычислить с помощью формулы:

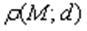 от точки
от точки  до прямой
до прямой 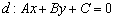 выражается формулой
выражается формулой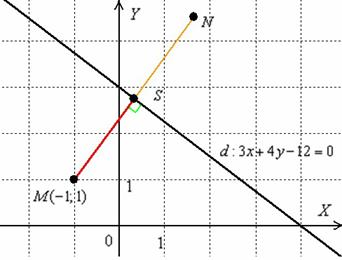
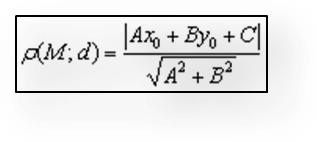
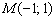 до прямой
до прямой 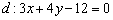
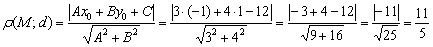
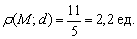

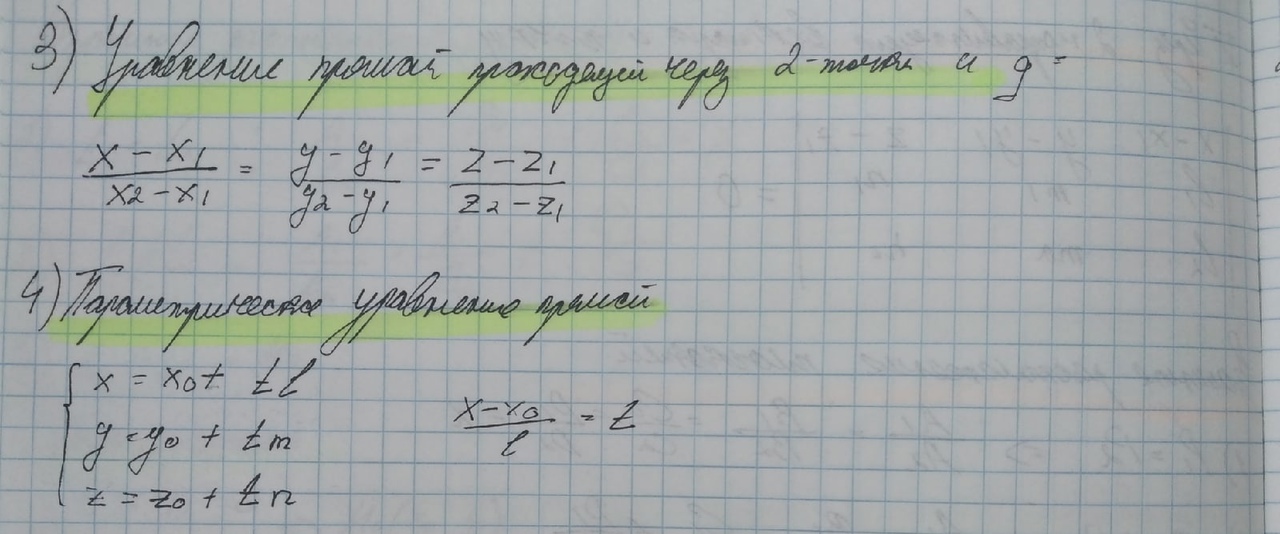


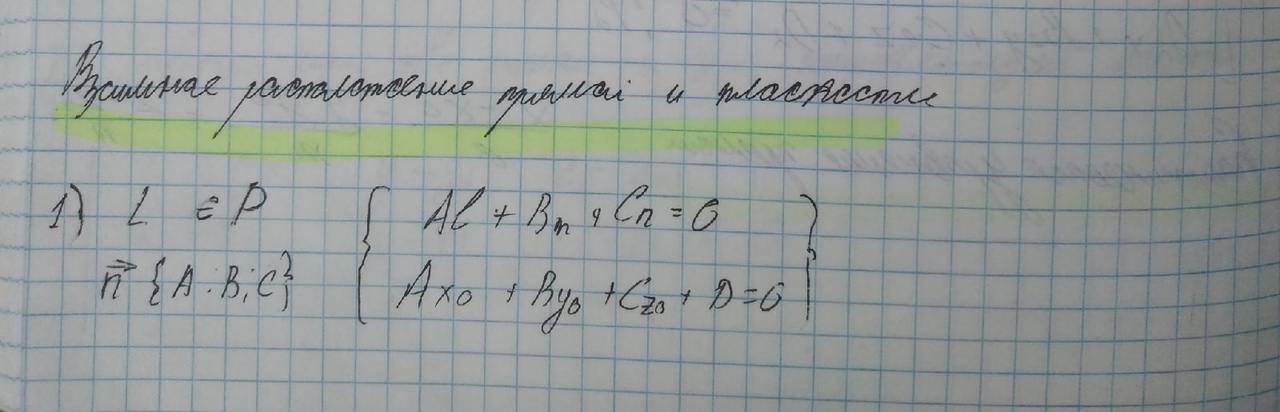

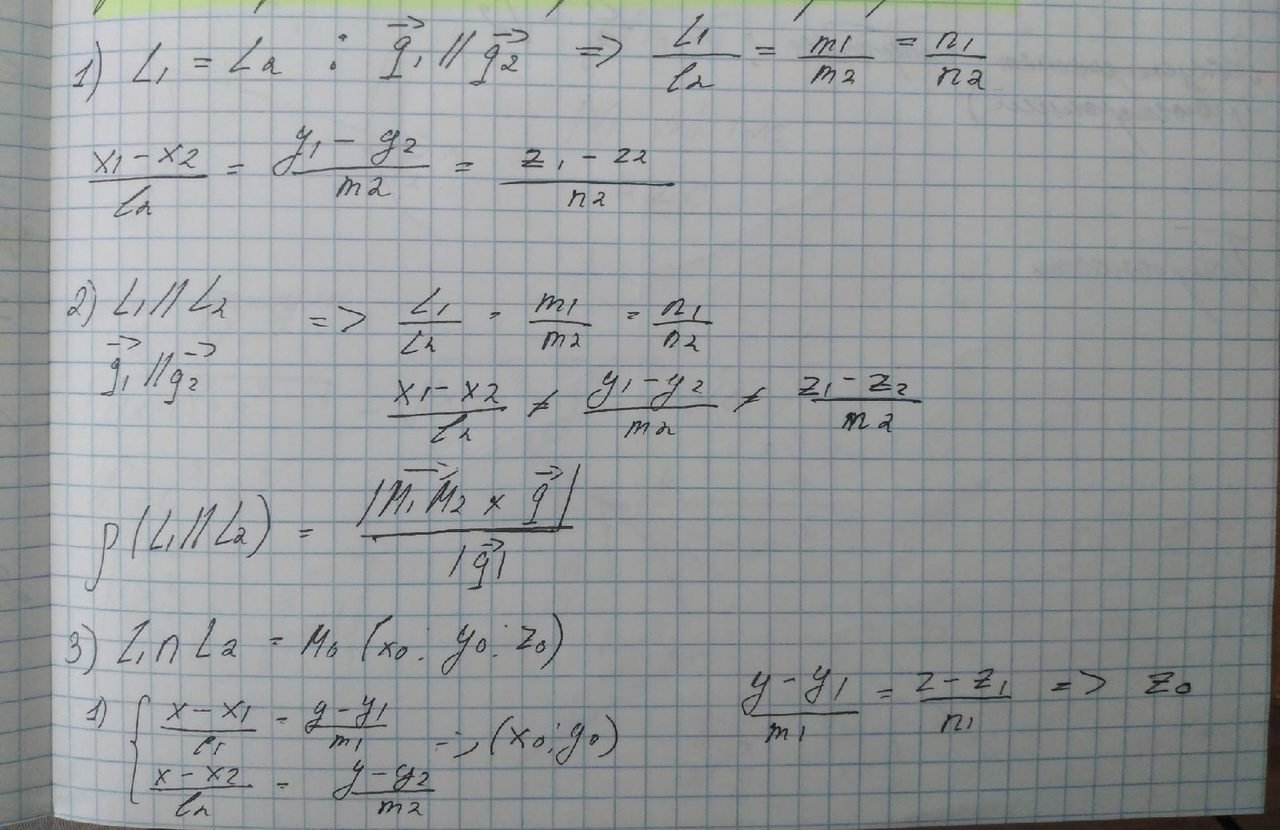

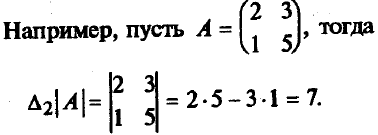
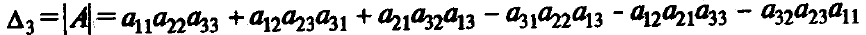


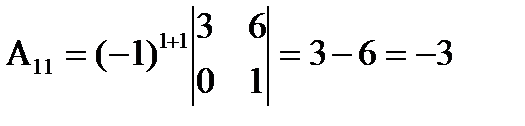 ;
; 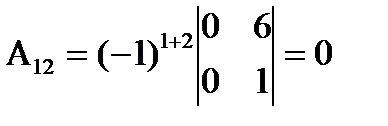 и т.д.
и т.д.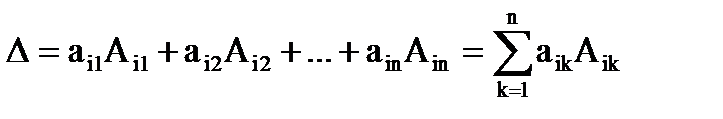 (разложение по элементам i-й строки;
(разложение по элементам i-й строки; 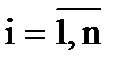 );
);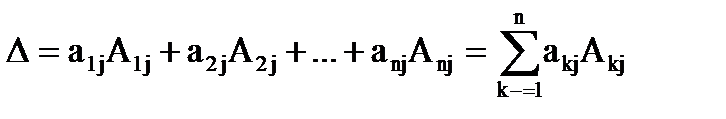 (разложение по элементам j-го столбца;
(разложение по элементам j-го столбца; 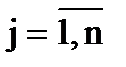 ).
).
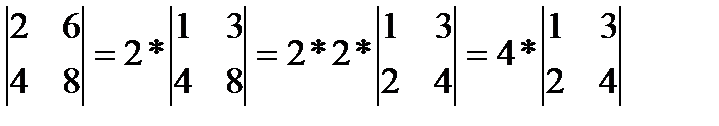 , но
, но 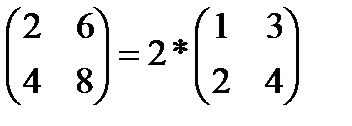 .
.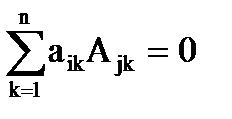 при i ¹ j.
при i ¹ j.