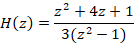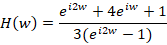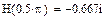Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В ычисляем расширенную неопределённость ⇐ ПредыдущаяСтр 3 из 3
Согласно заданию значение вероятности охвата P = 0,95, которое соответствует «результатам измерения общего назначения». Анализируя входные величины, отмечаем, что имеют место две составляющие суммарной неопределенности, одна из которых определена по тира А и имеет нормальный закон распределения, а другая – по типу В и имеет равномерный закон распределения. В этом случае коэффициент охвата принимаем равным квантилю распределения Стьюдента при вероятности охвата Р и эффективном числе степеней свободы ν eff, определяемом по формуле
Подставив числовые значения, получим:
νeff = (22-1)(0.405/0.284)4 = 86. Принимаем значение коэффициента охвата, равным k = 2 Определяем расширенную неопределённость по формуле: U(Y) = k×u(Y). (7) Получаем значение расширенной неопределённости: U(Y) = 2×0.405 = 0,91 Ом. Округляем данное значение по правилам округления результатов измерений, и получаем окончательное значение расширенной неопределённости: U(Y) = 0,9 Ом. 6 Записываем результат измерения с учётом неопределённости. Y = y ± U(Y) = (483,2 ± 0,9) Ом. Измеренное значение сопротивления равно (483,2 ± 0,9) Ом,, где число, стоящее после знака ± расширенная неопределенность U(Y) = k×u(Y), полученная для суммарной стандартной неопределённости 0,405 и коэффициента охвата k = 2, соответствующего уровню доверия 95 % для t-распределения с v = 86 степенями свободы. Рекомендуемая литература: 1 ГОСТ Р 34100.3-2017. Руководство ИСО/МЭК 98-3:2008. Неопределенность измерения. Часть 3. Руководство по выражению неопределенности измерений 2 Захаров И.П. Неопределенность измерений для чайников и … начальников: Учебное пособие / И.П. Захаров. – Харьков: 2013. – 56 с. 3 Бронштейн И.Н. Справочник по математике для инженеров и учащихся вузов / И.Н. Бронштейн, К.А. Семендяев. - М.: Наука, 1986.- 544 с. 4 Шишкин, И.Ф. Теоретическая метрология. Ч. 1. Общая теория измерений: Учебник для вузов / И.Ф. Шишкин. – СПб.: Питер, 2010. – 190 с. Раздел 3. «Преобразование и обработка сигналов»
Авторы задач: Щепетов Александр Григорьевич, профессор РГУ нефти и газа им. И.М. Губкина, e-mail: a-shchepetov@mail.ru, Ермолкин Олег Викторович, профессор РГУ нефти и газа им. И.М. Губкина, e-mail ove@mail.ru, Дьяченко Юрий Николаевич, доцент Санкт-Петербургского политехнического университета Петра Великого, e-mail: ydko@mail.ru., Барат Вера Александровна, доцент НИУ МЭИ, e-mail vera.barat@mail.ru
Общая характеристика: задания относятся к задачам преобразования и обработки измерительных сигналов.
Безынерционное преобразование случайного сигнала На вход нелинейного безынерционного ИУ с известной функцией преобразования
Рис. 1. Тогда событие Из этого уравнения можно определить ПРВ выходного сигнала Зная ПРВ выходного сигнала, можно определить все статистические характеристики этого сигнала, в том числе его математическое ожидание Их можно вычислить также по формулам, не требующим знания функции Если обратная статическая характеристика ИУ является неоднозначной и имеет N ветвей, то вместо формулы (3) нужно пользоваться общей формулой
где Задача 3.1. (Щепетов А.Г.) На вход безынерционного ИУ с квадратичной характеристикой
т.е. входной сигнал на интервале
Решение: Обратная статическая характеристика ИУ Поэтому формула (6) содержит два слагаемых и имеет вид где следует записать
Учитывая, что
На рис. 2, в показан график этой функции. Условие нормировки ПРВ выходного сигнала выполняется. Действительно,
Рис. 2
Математическое ожидание и дисперсию выходного сигнала вычислим по формулам (4)
Вычисления по формулам (5) приводят к таким же результатам
Инерционное преобразование периодического сигнала Задача 3.2. (Ермолкин О.В., Щепетов А.Г.) Определить реакцию прибора с передаточной функцией на периодический сигнал, представляющий собой последовательность однополярных прямоугольных импульсов (меандр) амплитуды Рис. 1
Покажем решение этой задачи разными способами [1].
Способ 1. Первый способ решения задачи основан напредставлении периодического входного сигнала где где Полагая начальные условия нулевыми, можно записать
Следовательно
где
Решение: Коэффициенты Фурье входного сигнала вычислим по формулам
где
Следовательно, разложение рассматриваемого входного сигнала
Вычислим переходную функцию ИУ
и найдем оригиналы слагаемых ряда (1)
Соответствующие оригиналы
Умножая обе части этого разложения на
решая которую, найдем значения коэффициентов разложения (7) Таким образом
Переходя в (1) к оригиналам, окончательно получим
С течением времени (при
На рис. 2 показаны графики рассматриваемых входного и выходного сигналов ИУ. Входной сигнал (меандр) показан сплошной кривой 1, установившийся выходной сигнал (10) - пунктирной кривой 2. Видно, что процесс установления выходного сигнала практически завершается уже по истечение половины периода входного сигнала
Рис. 2
К сожалению, установившийся выходной сигнал (10) получен в форме ряда.
Способ 2. Установившееся периодическое решение (10) можно получить, если воспользоваться полученными ранее результатами анализа реакции ИУ на гармонический сигнал единичной амплитуды Установившаяся реакция линейного инерционного ИУ на такой сигнал имеет вид (3.56)
где
Учитывая (1), вместо (10) для установившегося выходного сигнала получаем
В рассматриваемом случае имеем Следовательно Учитывая соотношения несложно доказать, что прежнее решение (10) и найденное решение (15) совпадают друг с другом.
Способ 3. Периодический сигнал можно представить в виде суммы базовых импульсов, сдвинутых друг относительно друга по оси времени на величину, кратную периоду сигнала где
где В рассматриваемом случае можно записать где Тогда изображение реакции ИУ на первый импульс имеет вид
где
Переходя в (20) к оригиналам, найдем реакцию ИУ на первый импульс входного сигнала
то есть,
На рис. 3 показаны графики базового импульса входного сигнала 1 и реакции ИУ на этот импульс 2, построенной по формуле (22). Реакция ИУ на второйимпульс входного сигнала равна
Суммируя отклики ИУ на все импульсы входного сигнала, получим выходной сигнал ИУ
где
Выполняя суммирование этого ряда, можно показать, что с течением времени выходной сигнал ИУ оказывается периодическим и имеет тот же период
где
Способ 4. В заключение рассмотрим еще один способ решения задачи, позволяющий достаточно просто (без суммирования рядов) определить установившийся периодический выходной сигнал ИУ в аналитическом виде. Этот способ основан на методе вариации произвольных постоянных, который применяется при решении неоднородных дифференциальных уравнений. Для этого запишем, учитывая вид передаточной функции ИУ
Переходя во временную область и полагая, что начальные условия, наложенные на выходной сигнал, нулевые (т.е. считая, что Вновь перейдем в операторную область, полагая, что упомянутые выше начальные условия ненулевые (т.е., полагая, что из которого следует
Оригинал, соответствующий первому слагаемому в формуле (П2.67), найдем с помощью теоремы умножения. Второе слагаемое имеет табличный оригинал, то есть Выбор начального условия (т.е. выбор значения Кроме того, будем считать, что период
Отсюда найдем Первое слагаемое в формуле (33) есть ранее найденная реакция ИУ (21) на базовый импульс входного сигнала, т.е. вместо (33) можно записать
После приведения подобных членов формулы (34) совпадают с формулами (25).
Примечание: 1) Если При увеличении коэффициента k снижается постоянная времени ИУ. В этом случае форма установившегося выходного сигнала ИУ приближается к форме кходного сигнала. 2) при решении задачи для ИУ
Литература
Восстановление сигнала
Задача 3.3. (Дьяченко Ю.Н.): Основная полоса частот аналогового сигнала расположена в диапазоне от 0 до fm = 120Гц, частота дискретизации и обновления отсчетов на выходе ЦАП fS = 1200Гц, суммарная частотная погрешность от спада АЧХ в рабочем диапазоне Учесть, что в процессе ЦА преобразования дискретного цифрового сигнала в ступенчатый аналоговый сигнал, спектр исходного дискретного сигнала умножается на sinc-функцию вида Ответ: n =3, 273 < f с < 331Гц.
Покажем решение задачи в ее общей постановке [1]: Основная полоса частот аналогового сигнала расположена в диапазоне В ходе дискретизации непрерывный аналоговый сигнал преобразуется в отсчеты, следующие с частотой дискретизации Практическое восстановление аналогового сигнала по дискретным отсчетам производится с использованием ЦАП, на выходе которого формируется ступенчатое напряжение в виде кусочно-постоянной кривой. В частотной области ЦАП выполняет функции ФНЧ с АЧХ вида При переходе от дискретного к ступенчатому сигналу ослабляются высокочастотные составляющие дискретного сигнала расположенные вблизи частот Результат поясняет рис.1. На нем штриховой линией 2 изображен график функции (3)
Рис.1. К иллюстрации расчета сглаживающего ФНЧ
Улучшить результаты восстановления можно двумя путями: во-первых, использовать ФНЧ высокого порядка, во-вторых, повысить частоту дискретизации (т.е. увеличить отношение Рассмотрим методику определения параметров фильтра при условии, что используется ФНЧ с АЧХ Баттерворта где Амплитудный спектр
Относительная погрешность АЧХ ФНЧ на частоте После подстановки Окончательно для минимального значения частоты среза Ослабление высокочастотных гармоник дискретного сигнала, не входящих в спектр исходного сигнала, происходит при его преобразовании в ступенчатую форму и дальнейшем сглаживании ФНЧ. Общий коэффициент подавления высокочастотных гармоник относительно низкочастотных составляющих полезного сигнала определяется величиной обратной произведению функции Неравенство (6) означает, что на наиболее низкой частоте подавляемых гармоник Введем обозначение
Окончательно для определения максимального значения частоты среза Расчет ФНЧ удобно проводить по формулам (5) и (7) посредством простого перебора значений его порядка и определения наименьшего
Рекомендуемая литература: 1. Щепетов А.Г., Дьяченко Ю.Н. Преобразование измерительных сигналов: учебник и практикум для академического бакалавриата по инженерно-техническим направлениям и специальностям / под ред. А. Г. Щепетова. – Москва: Юрайт, 2016 – 269 с. 2. Айфичер Э.С., Джевис Б.У. Цифровая обработка сигналов: практический подход, 2-е издание.: Пер. с англ. – М.: Издательский дом «Вильямс», 2004. – 992 с.
Задача 3.4: (Барат В.А.) Дискретный сигнал x(n)=sin(0.5πn) сначала интегрируется, а затем дифференцируется. Определите аналитическое выражение выходного сигнала, если для цифрового интегрирования используется метод Симпсона, а дифференциатор можно считать идеальным. Интегрирование по методу Симпсона определяется при помощи разностного уравнения y[n]=y[n-2]+1/3(x[n]+4x[n-1]+x[n-2]) Построим передаточную функцию интегратора при помощи z-преобразования
подставляя z=eiw получаем
Амплитудно-частотная и фазо-частотная характеристики
Комплексный коэффициент передачи на частоте входного сигнала равен После интегрирования получаем сигнал y1(n)=0.667sin(0,5πn-90°)
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 245; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.154.103 (0.191 с.) |
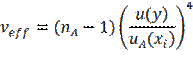
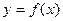 поступает случайный сигнал
поступает случайный сигнал 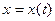 , одномерная функция плотности распределения вероятностей (ПРВ) которого
, одномерная функция плотности распределения вероятностей (ПРВ) которого 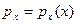 известна. Требуется определить статистические характеристики выходного сигнала: ПРВ
известна. Требуется определить статистические характеристики выходного сигнала: ПРВ 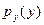 , математическое ожидание
, математическое ожидание 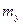 и дисперсию
и дисперсию 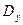 . Пусть функция
. Пусть функция 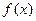 обладает свойством изоморфизма, т.е. существует однозначная обратная функция (рис.1)
обладает свойством изоморфизма, т.е. существует однозначная обратная функция (рис.1)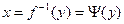 . (1)
. (1)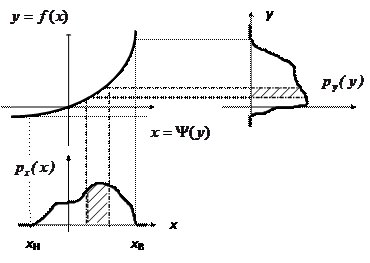
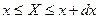 равносильно событию
равносильно событию 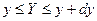 , что означает равенство вероятностей этих событий. Поэтому площади заштрихованных фигур на рис. 1 равны друг другу
, что означает равенство вероятностей этих событий. Поэтому площади заштрихованных фигур на рис. 1 равны друг другу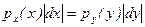 . (2)
. (2) 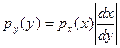 , или
, или 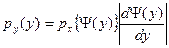 . (3)
. (3)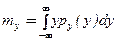 ,
, 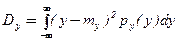 . (4)
. (4)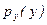 , что можно использовать для контроля правильности расчетов
, что можно использовать для контроля правильности расчетов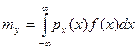 ,
, 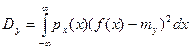 (5)
(5)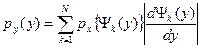 , (6)
, (6)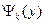 - k - ая ветвь обратной статической характеристики ИУ (1). При правильных расчетах должно выполняться условие нормировки ПРВ. Покажем пример решения такой задачи [1].
- k - ая ветвь обратной статической характеристики ИУ (1). При правильных расчетах должно выполняться условие нормировки ПРВ. Покажем пример решения такой задачи [1].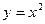 поступает случайный сигнал
поступает случайный сигнал 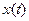 , ПРВ которого имеет вид
, ПРВ которого имеет вид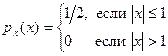 , (7)
, (7)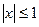 имеет равномерное распределение (рис. 2, а). Нужно определить статистические характеристики выходного сигнала: плотность распределения вероятностей
имеет равномерное распределение (рис. 2, а). Нужно определить статистические характеристики выходного сигнала: плотность распределения вероятностей 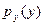 , математическое ожидание
, математическое ожидание  является неоднозначной, так как имеет две ветви (рис.2,б)
является неоднозначной, так как имеет две ветви (рис.2,б) и
и 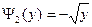 .
.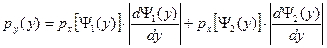 ,
,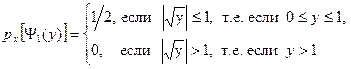 ,
,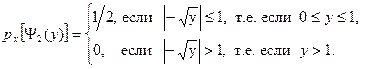
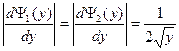 , можно записать
, можно записать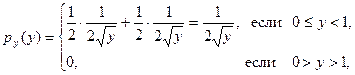 .
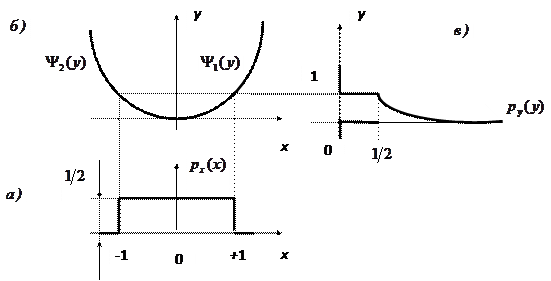
.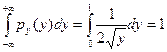 .
.
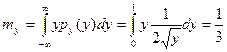 ,
,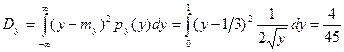 .
.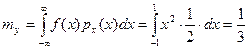 ,
,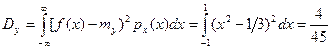 .
.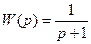 ,
, 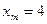 и длительности
и длительности 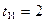 с, следующих друг за другом с интервалом 2 с (рис.1).
с, следующих друг за другом с интервалом 2 с (рис.1).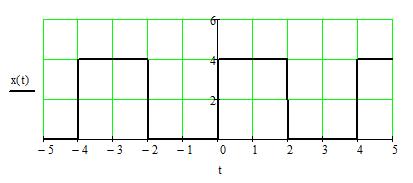
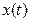 в форме тригонометрического ряда Фурье
в форме тригонометрического ряда Фурье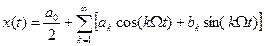 , (1)
, (1) - коэффициенты Фурье. В соответствии с принципом суперпозиции, реакция линейного ИУ на такой сигнал равна сумме реакций на каждую из составляющих ряда (1) в отдельности, т.е.
- коэффициенты Фурье. В соответствии с принципом суперпозиции, реакция линейного ИУ на такой сигнал равна сумме реакций на каждую из составляющих ряда (1) в отдельности, т.е. , (2)
, (2)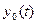 - реакция ИУ на единичный ступенчатый сигнал
- реакция ИУ на единичный ступенчатый сигнал 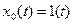 ;
; 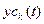 и
и 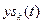 - реакции ИУ на гармонические составляющие сигнала
- реакции ИУ на гармонические составляющие сигнала 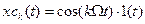 и
и 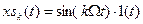 соответственно.
соответственно.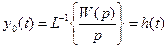 ;
;  ;
; 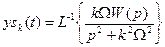 .
.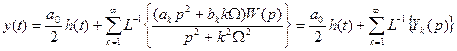 , (3)
, (3)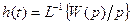 - переходная функция ИУ;
- переходная функция ИУ; 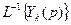 - оригиналы соответствующих изображений, зависящие от вида передаточной функции ИУ
- оригиналы соответствующих изображений, зависящие от вида передаточной функции ИУ 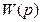 и формы базового импульса входного сигнала. Покажем применение этих формул для решения рассматриваемой задачи.
и формы базового импульса входного сигнала. Покажем применение этих формул для решения рассматриваемой задачи.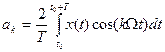 , где
, где 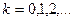 ,
, 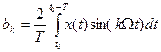 , где
, где 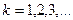 .
. 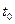 – произвольное число, которое можно выбирать из соображений удобства вычисления. Значение этого числа обычно выбирают так, чтобы функция
– произвольное число, которое можно выбирать из соображений удобства вычисления. Значение этого числа обычно выбирают так, чтобы функция 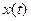 на отрезке
на отрезке 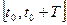 не имела особенностей. Полагая в приведенных формулах
не имела особенностей. Полагая в приведенных формулах 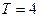 ,
, 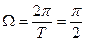 ,
, 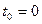 .В результате получим
.В результате получим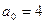 ,
, 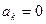 ,
, 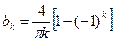 , то есть
, то есть 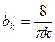 , где
, где  (4)
(4) 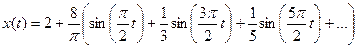 . (5)
. (5)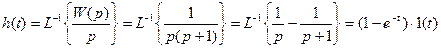 (6)
(6)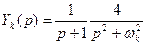 , где
, где 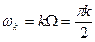 ,
, 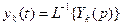 определим с помощью теоремы разложения. Для этого воспользуемся разложением
определим с помощью теоремы разложения. Для этого воспользуемся разложением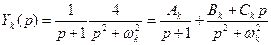 . (7)
. (7)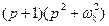 и приравнивая коэффициенты в обеих частях полученного равенства при одинаковых степенях
и приравнивая коэффициенты в обеих частях полученного равенства при одинаковых степенях 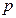 , получим систему уравнений
, получим систему уравнений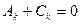 ,
, 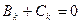 ,
, 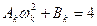 ,
,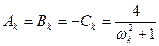 .
.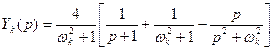 . (8)
. (8)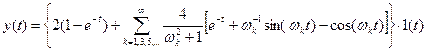 . (9)
. (9)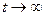 ) в выходном сигнале ИУ исчезают составляющие с экспоненциальным множителем
) в выходном сигнале ИУ исчезают составляющие с экспоненциальным множителем 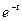 и он становится периодическим. (рис. 2). Этот установившийся периодический выходной сигнал имеет вид
и он становится периодическим. (рис. 2). Этот установившийся периодический выходной сигнал имеет вид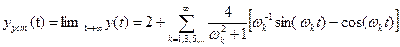 . (10)
. (10)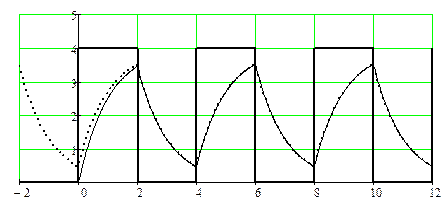
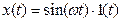 , (11)
, (11)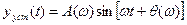 , (12)
, (12)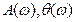 - соответственно модуль и аргумент комплексной частотной характеристики ИУ
- соответственно модуль и аргумент комплексной частотной характеристики ИУ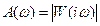 ,
, 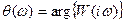 . (13)
. (13)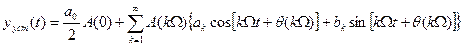 . (14)
. (14)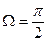 ,
,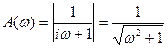 ,
, 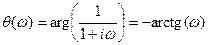 .
.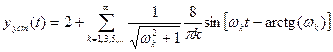 . (15)
. (15)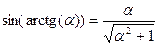 и
и 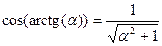 ,
,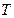 , т.е.
, т.е.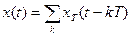 , (16)
, (16)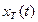 - базовый импульс сигнала. Реакция линейного ИУ на такой входной сигнал равна сумме реакций ИУ на каждый из импульсов в отдельности, т.е.
- базовый импульс сигнала. Реакция линейного ИУ на такой входной сигнал равна сумме реакций ИУ на каждый из импульсов в отдельности, т.е.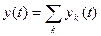 , (17)
, (17)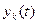 - реакция ИУ на
- реакция ИУ на 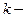 ый «сдвинутый» базовый импульс входного сигнала
ый «сдвинутый» базовый импульс входного сигнала .
.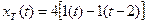 , (18)
, (18) - единичная ступенчатая функция времени (1.10). Соответствующее изображение по Лапласу базового импульса равно
- единичная ступенчатая функция времени (1.10). Соответствующее изображение по Лапласу базового импульса равно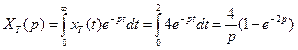 . (19)
. (19)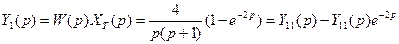 , (20)
, (20) .
.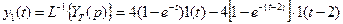 . (21)
. (21)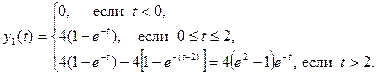 (22)
(22) 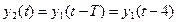 и т.д., реакция на
и т.д., реакция на 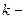 ый импульс
ый импульс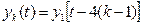 . (23)
. (23)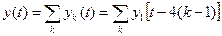 , (24)
, (24)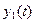 вычисляется по формуле (21).
вычисляется по формуле (21).

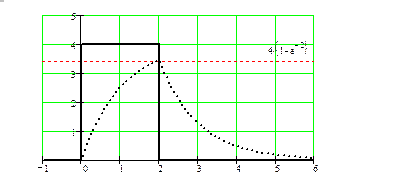 Рис. 3.
Рис. 3. , что и входной сигнал, а его базовый импульс
, что и входной сигнал, а его базовый импульс 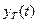 вычисляется по формулам
вычисляется по формулам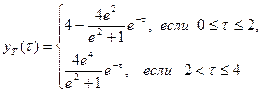 , (25)
, (25)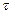 - время, отсчитываемое от момента установления периодического выходного сигнала ИУ. Формулы (25), в отличие от (13) и (14), определяют установившийся выходной сигнал ИУ в аналитическом виде.
- время, отсчитываемое от момента установления периодического выходного сигнала ИУ. Формулы (25), в отличие от (13) и (14), определяют установившийся выходной сигнал ИУ в аналитическом виде.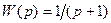 , операционное уравнение, связывающее изображения входного и выходного сигналов ИУ
, операционное уравнение, связывающее изображения входного и выходного сигналов ИУ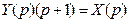 , т.е.
, т.е. 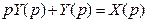 . (26)
. (26)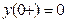 ), получим дифференциальное уравнение ИУ
), получим дифференциальное уравнение ИУ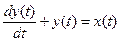 . (27)
. (27) ). В этом случае вместо (26) получим другое уравнение
). В этом случае вместо (26) получим другое уравнение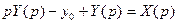 , (28)
, (28)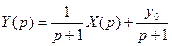 . (29)
. (29)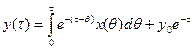 . (30)
. (30)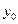 , входящего в формулу (24)) подчиним условию периодичности установившегося выходного сигнала
, входящего в формулу (24)) подчиним условию периодичности установившегося выходного сигнала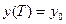 . (31)
. (31)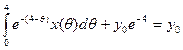 . (32)
. (32)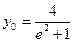 . Возвращаясь к (30), получим
. Возвращаясь к (30), получим 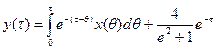 . (33)
. (33) . (34)
. (34)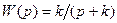 , то вместо (30) можно получить
, то вместо (30) можно получить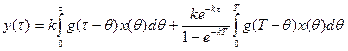
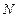 - го порядка изображение (29) содержит
- го порядка изображение (29) содержит 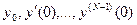 , а условие периодичности (31) заменяется
, а условие периодичности (31) заменяется 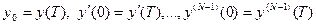 .
.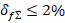 , подавление высокочастотных составляющих спектра от частоты fS - fm и выше — не менее q = 50 дБ. Найдите минимальный порядок n и частоту среза f с сглаживающего ФНЧ с АЧХ Баттерворта
, подавление высокочастотных составляющих спектра от частоты fS - fm и выше — не менее q = 50 дБ. Найдите минимальный порядок n и частоту среза f с сглаживающего ФНЧ с АЧХ Баттерворта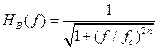 .
.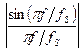 .
.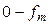 , частота дискретизации и обновления отсчетов
, частота дискретизации и обновления отсчетов 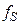 , суммарная частотная погрешность от спада АЧХ в рабочем диапазоне не более
, суммарная частотная погрешность от спада АЧХ в рабочем диапазоне не более 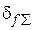 %(относительное значение), подавление высокочастотных составляющих спектра от частоты
%(относительное значение), подавление высокочастотных составляющих спектра от частоты 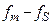 и выше не менее
и выше не менее 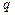 дБ. Найти минимальный порядок
дБ. Найти минимальный порядок 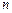 и частоту среза
и частоту среза 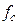 ФНЧ.
ФНЧ.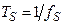 во временной области). Если спектр
во временной области). Если спектр 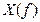 исходного сигнала расположен в диапазоне частот от 0 до
исходного сигнала расположен в диапазоне частот от 0 до 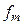 , то спектр дискретного сигнала
, то спектр дискретного сигнала 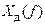 содержит еще и копии этого спектра, расположенные на частотной оси в диапазонах от
содержит еще и копии этого спектра, расположенные на частотной оси в диапазонах от 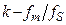 до
до 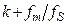 , где
, где 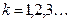 (в соответствии с рис. 1, где сами эти спектры не показаны). Восстановить аналоговый сигнал по отсчетам можно, если без искажений выделить его спектр
(в соответствии с рис. 1, где сами эти спектры не показаны). Восстановить аналоговый сигнал по отсчетам можно, если без искажений выделить его спектр 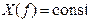 в заданном диапазоне.
в заданном диапазоне.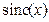 . Следовательно, амплитудный спектр ступенчатого сигнала
. Следовательно, амплитудный спектр ступенчатого сигнала 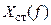
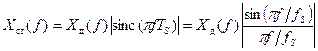 . (1)
. (1)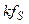 кратных частоте дискретизации. Однако, появляется спад АЧХ в основном частотном диапазоне
кратных частоте дискретизации. Однако, появляется спад АЧХ в основном частотном диапазоне 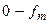 , следовательно, и частотная погрешность, относительное значение которой равно
, следовательно, и частотная погрешность, относительное значение которой равно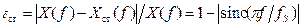 . (2)
. (2)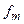 . На рис. 1 кривой 3 изображен график АЧХ простейшего ФНЧ 1-го порядка, а кривой 1 - график спектра выходного сглаженного сигнала.
. На рис. 1 кривой 3 изображен график АЧХ простейшего ФНЧ 1-го порядка, а кривой 1 - график спектра выходного сглаженного сигнала.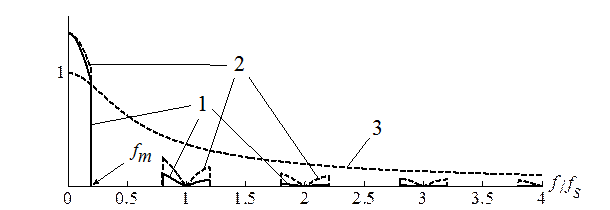
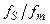 ). Первый путь приводит к усложнению схемы ФНЧ и ее настройки, ухудшению стабильности характеристик фильтра, появлению значительных фазовых искажений сигнала и задержке его во времени. Поэтому рационально определить разумное соотношение между параметрами ФНЧ и частотой
). Первый путь приводит к усложнению схемы ФНЧ и ее настройки, ухудшению стабильности характеристик фильтра, появлению значительных фазовых искажений сигнала и задержке его во времени. Поэтому рационально определить разумное соотношение между параметрами ФНЧ и частотой 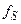 .
.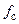 и n – частота среза и порядок фильтра.
и n – частота среза и порядок фильтра.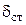 по формуле (2). ФНЧ вносит дополнительное ослабление основного спектра сигнала, максимальное допустимое значение которого можно записать в виде погрешности
по формуле (2). ФНЧ вносит дополнительное ослабление основного спектра сигнала, максимальное допустимое значение которого можно записать в виде погрешности 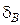 (значение
(значение 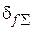 предварительно переводится из процентов в относительные единицы):
предварительно переводится из процентов в относительные единицы):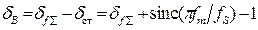 .
.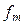 не должна превышать значение
не должна превышать значение 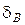 :
: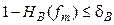 . (4)
. (4)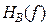 из формулы (3) в соотношение (4) и простых преобразований последнего с учетом
из формулы (3) в соотношение (4) и простых преобразований последнего с учетом 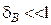 , получим:
, получим: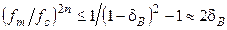 .
.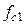 фильтра получим
фильтра получим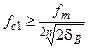 . (5)
. (5) из (1) и АЧХ фильтра (3):
из (1) и АЧХ фильтра (3):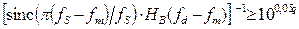 (6)
(6)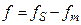 , значение коэффициента подавления не меньше заданного
, значение коэффициента подавления не меньше заданного 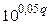 , пересчитанного из логарифмических единиц (дБ) в относительные единицы.
, пересчитанного из логарифмических единиц (дБ) в относительные единицы.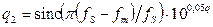 , определяющее необходимое значение коэффициента подавления ФНЧ. Тогда из соотношения (6) с учетом (3) и того, что в практических задачах
, определяющее необходимое значение коэффициента подавления ФНЧ. Тогда из соотношения (6) с учетом (3) и того, что в практических задачах 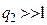 , получим:
, получим: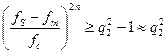 .
.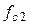 фильтра получим соотношение
фильтра получим соотношение . (7)
. (7)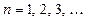 , при котором частоту среза
, при котором частоту среза 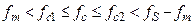 .
.