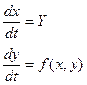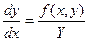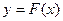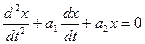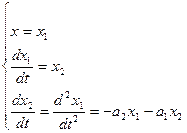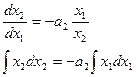Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь устойчивости с корнями характеристического уравненияСтр 1 из 4Следующая ⇒
Связь устойчивости с корнями характеристического уравнения Существуют следующие способы определения устойчивости: 1) прямой – путем решения дифференциального уравнения и анализа этого уравнения; 2) по корням характеристического уравнения; 3) по критериям устойчивости. Рассмотрим способ 2. Пусть динамика САУ описывается уравнением:
Приложим к системе внешнее воздействие, а затем снимем его. Это будет соответствовать нулевой правой части.
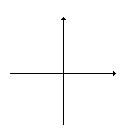
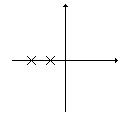
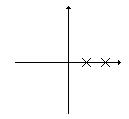
Корни характеристического уравнения определяют вид переходной составляющей в решении дифференциального уравнения. Проанализируем поведение системы для различных корней: 1) вещественный корень а) б) в)
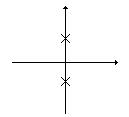
2) Пара комплексно-сопряженных корней В решении имеем составляющую вида: а) б) в)
г)
Вывод: для устойчивости САУ необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательную вещественную часть. Реальные системы нелинейны и мы проводим их линеаризацию. Чтобы распространить сделанные выводы о корнях на линеаризованные системы, А.А. Ляпунов доказал следующие теоремы: I теорема: Если линеаризованная система устойчива, то никакие из отброшенных при линеаризации корней не могут сделать ее неустойчивой. II теорема: Если линеаризованная система неустойчива, то никакие из отброшенных при линеаризации корней не могут сделать ее устойчивой. III теорема: Если линеаризованная система находится на грани устойчивости, то устойчивость реальной системы определяется корнями, отброшенными при линеаризации.
Критерии устойчивости
Критерии – это признаки, по которым можно судить об устойчивости системы без решения дифференциального уравнения динамики системы и без вычисления корней.
Все критерии делятся на алгебраические, которые основаны на анализе коэффициентов характеристического уравнения, и частотные, которые основаны на анализе частотных характеристик системы. 1. Алгебраические критерии устойчивости. Критерий Стодолы (простейший алгебраический критерий). Простейшим необходимым, но недостаточным критерием устойчивости является требование того, чтобы все коэффициенты характеристического уравнения имели одинаковый знак. Докажем это. Пусть имеем устойчивую систему с характеристическим уравнением:
В устойчивой системе все корни имеют отрицательную вещественную часть:
Запишем выражение (1) через корни:
Подставим значения корней:
Раскроем скобки и приведем к виду выражения (1). Перемножая или складывая положительные числа нельзя получить отрицательные, то есть все коэффициенты будут положительные или все отрицательные (в зависимости от а n). Для систем 1-го и 2-го порядков критерий является необходимым и достаточным. Для систем более высокого порядка этот критерий является необходимым, но не достаточным. Если хоты бы один коэффициент характеристического уравнения имеет знак отличный от знаков других коэффициентов, то можно сразу сказать, что система неустойчива и никаких дополнительных исследований не потребуется проводить. Но положительность всех коэффициентов не гарантирует устойчивости. При некотором соотношении корней с положительной вещественной частью можно тоже получить все коэффициенты одного знака. Здесь требуются дополнительные исследования. Были разработаны другие алгебраические критерии, которые являются как необходимыми, так и достаточными. Наибольшее распространение получили критерий Рауса(E.I. Routh 1877г.) и критерий Гурвица (A.Hurwitz 1895г.). Оба критерия основаны на построении определителей из коэффициентов характеристического уравнения. В результате они приводят к одной и той же системе неравенств.
Критерий Гурвица
Определитель Гурвица составляется по следующему правилу: главная диагональ определителя размером n x n последовательно заполняется коэффициентами характеристического уравнения, начиная с коэффициента при (n-1) производной до свободного члена. Столбцы вверх от главной диагонали дополняют последовательно коэффициентами с возрастающими индексами, а столбцы вниз – коэффициентами с убывающими индексами. Места, которые должны быть заняты коэффициентами с индексом выше а n и ниже а0, заполняют нулями.
Формулировка: Для того, чтобы характеристическое уравнение системы имело все корни с отрицательной вещественной частью необходимо, чтобы главный определитель Гурвица и все его диагональные миноры Dn-1, Dn-1, …, D2, D1 имели один знак с коэффициентом при старшей производной. Пример: 1. Система 1-го порядка.
2. Система 2-го порядка.
3. Система 3-го порядка.
Достоинства критерия: 1. Сравнительная простота. Недостатки: 1. Громоздкость вычислений при n>4. 2. Алгебраические критерии дают ответ на вопрос, устойчива система или нет, но ничего не говорят о том, что надо сделать, чтобы система стала устойчивой. С инженерной точки зрения более применим частотный критерий устойчивости.
Принцип аргумента Пусть дано характеристическое уравнение:
Это уравнение можно записать через его корни:
где a 1, a 2, …, a n - корни полинома D (p). Выполним подстановку
Представим элементарный множитель (
Суммарный угол поворота равен 1800. Для корня с отрицательной вещественной частью вектор (
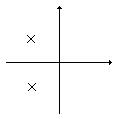
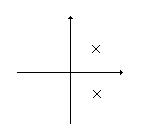
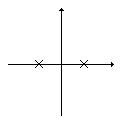
Используя принцип аргумента, исследуем поведение функции Для любого значения частоты w имеем вектор, который будет поворачиваться при изменении частоты. Траектория конца вектора называется годографом Михайлова. Принцип аргумента позволяет сформулировать критерий устойчивости Михайлова: САУ будет устойчива, если годограф функции Пример устойчивых:
Пример неустойчивых:
Если годограф проходит через начало координат, то система находится на границе устойчивости.
Условие нахождения на границе устойчивости: Формулировка может звучать иначе:
Для устойчивой САУ годограф начинается на вещественной положительной полуоси и должен поочередно пересекать мнимую и вещественную ось.
Для устойчивой САУ вещественные и мнимые части годографа Михайлова должны по очереди пересекать ось абсцисс.
При наличии астатических и Диаграмма Вишнеградского Рассмотрим характеристическое уравнение 3-го порядка:
Получим: По критерию Гурвица граница устойчивости будет иметь уравнение: Далее разбиваем область устойчивости на три подобласти:
I область: ближайший к началу координат корень – комплексный. Переходный процесс будет колебательным.
II область: экспоненциально-колебательный переходный процесс.
III область: апериодический переходный процесс.
IV область: переходный процесс расходится. Далее диаграмма Вишнеградского была доработана и вся область разбита вспомогательными линиями, позволяющими оценить быстродействие, запас устойчивости и колебательности. Особенности нелинейных САУ 1. Не действует принцип суперпозиции. В линейных САУ принцип суперпозиции позволял вычислять реакцию системы на сумму нескольких воздействий как сумму реакции на некоторое воздействие. В линейных САУ, при увеличении входного сигнала выходной сигнал увеличивался пропорционально, то есть характер переходных процессов (форма графика и устойчивость) не изменяются. В нелинейной САУ реакция на сумму воздействий не равна сумме реакций на отдельное воздействие:
2. В нелинейных САУ характер движения зависит и от формы входного сигнала и от его амплитуды.
САУ устойчива в “малом” и неустойчива в “большом”
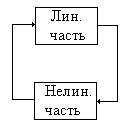
3. Для нелинейных САУ характерным является режим незатухающих колебаний, возникающих из самого принципа работы. В этом случае мы не можем получить какого-то постоянного значения выходной величины. Автоколебания могут быть одночастотными и многочастотными. На одних частотах колебания будут устойчивыми, на других – нет. 4. В нелинейных САУ при затухании колебаний происходит изменение частоты колебаний. 5. Соединения нелинейных звеньев обладают рядом особенностей: I. Некоммутативность (переставлять нельзя!). II. Не всегда существует обратный оператор (у линейных В результате выделяют два класса нелинейных систем: I класс: удается сгруппировать все линейные звенья в одну группу, нелинейные – в другую.
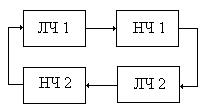
II класс: есть несколько групп линейных и нелинейных звеньев и они чередуются между собой.
Метод фазовой плоскости
Состояние САУ в любой момент времени характеризуется значением выходной координаты и (n -1) ее производных. В результате образуется n -мерное пространство, которое называется базовым. Точка, указывающее текущее состояние системы, называется изображающей.
Переходному процессу в системе будет соответствовать перемещение изображающей точки по фазовой траектории. Множество фазовых траекторий для различных начальных условий называется базовым фазовым портретом САУ. Метод визуальный, поэтому наглядность обеспечивается только для 2-го порядка. Уравнение 2-го порядка в нормальной форме Коши записывается в следующем виде:
Исключаем время (делим 2-е уравнение на 1-е): Далее решаем это уравнение. Уравнение фазовой траектории будет иметь вид: Исследуем линейную систему 2-го порядка методом фазовой плоскости:
Представим исходную систему в форме Коши:
Исключаем время: В зависимости от расположения корней характеристического уравнения и различных соотношениях a 1 и a 2 получаем 6 видов фазовых портретов.
Особая точка – это такая точка на фазовой траектории, где уравнение движения не определено (или направление). Реальные системы считают линейными в окрестности рабочей точки. За пределами этой области, вследствие значительного отклонения характеристик от линейных, картина фазовых траекторий может стать качественно иной. В НС на фазовых портретах появятся дополнительные фазовые траектории называющиеся особыми линиями. Особая линия – это замкнутая фазовая траектория, которая ограничивает области с различным поведением системы. Имеет место 4 вида особых линий: 1. Устойчивый предельный цикл – замкнутая фазовая траектория, за пределами которой процесс сходится, а внутри расходится.
2. Неустойчивый предельный цикл - замкнутая фазовая траектория, за пределами которой процесс расходится, а внутри сходится.
3. Сепаратрисса – образована двумя особыми точками центр и 2 седла.
4. Зона застоя (такие линии характерны в системах с зоной нечувствительности и трением). Установившемуся состоянию соответствует не одна точка, а область. Особая точка вытягивается в особый отрезок.
Связь устойчивости с корнями характеристического уравнения Существуют следующие способы определения устойчивости: 1) прямой – путем решения дифференциального уравнения и анализа этого уравнения; 2) по корням характеристического уравнения; 3) по критериям устойчивости.
Рассмотрим способ 2. Пусть динамика САУ описывается уравнением:
Приложим к системе внешнее воздействие, а затем снимем его. Это будет соответствовать нулевой правой части.
Корни характеристического уравнения определяют вид переходной составляющей в решении дифференциального уравнения. Проанализируем поведение системы для различных корней: 1) вещественный корень а) б) в)
2) Пара комплексно-сопряженных корней В решении имеем составляющую вида: а) б) в)
г)
Вывод: для устойчивости САУ необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательную вещественную часть. Реальные системы нелинейны и мы проводим их линеаризацию. Чтобы распространить сделанные выводы о корнях на линеаризованные системы, А.А. Ляпунов доказал следующие теоремы: I теорема: Если линеаризованная система устойчива, то никакие из отброшенных при линеаризации корней не могут сделать ее неустойчивой. II теорема: Если линеаризованная система неустойчива, то никакие из отброшенных при линеаризации корней не могут сделать ее устойчивой. III теорема: Если линеаризованная система находится на грани устойчивости, то устойчивость реальной системы определяется корнями, отброшенными при линеаризации.
Критерии устойчивости
Критерии – это признаки, по которым можно судить об устойчивости системы без решения дифференциального уравнения динамики системы и без вычисления корней. Все критерии делятся на алгебраические, которые основаны на анализе коэффициентов характеристического уравнения, и частотные, которые основаны на анализе частотных характеристик системы. 1. Алгебраические критерии устойчивости. Критерий Стодолы (простейший алгебраический критерий). Простейшим необходимым, но недостаточным критерием устойчивости является требование того, чтобы все коэффициенты характеристического уравнения имели одинаковый знак. Докажем это. Пусть имеем устойчивую систему с характеристическим уравнением:
В устойчивой системе все корни имеют отрицательную вещественную часть:
Запишем выражение (1) через корни:
Подставим значения корней:
Раскроем скобки и приведем к виду выражения (1). Перемножая или складывая положительные числа нельзя получить отрицательные, то есть все коэффициенты будут положительные или все отрицательные (в зависимости от а n). Для систем 1-го и 2-го порядков критерий является необходимым и достаточным. Для систем более высокого порядка этот критерий является необходимым, но не достаточным. Если хоты бы один коэффициент характеристического уравнения имеет знак отличный от знаков других коэффициентов, то можно сразу сказать, что система неустойчива и никаких дополнительных исследований не потребуется проводить. Но положительность всех коэффициентов не гарантирует устойчивости. При некотором соотношении корней с положительной вещественной частью можно тоже получить все коэффициенты одного знака. Здесь требуются дополнительные исследования. Были разработаны другие алгебраические критерии, которые являются как необходимыми, так и достаточными. Наибольшее распространение получили критерий Рауса(E.I. Routh 1877г.) и критерий Гурвица (A.Hurwitz 1895г.). Оба критерия основаны на построении определителей из коэффициентов характеристического уравнения. В результате они приводят к одной и той же системе неравенств.
Критерий Гурвица
Определитель Гурвица составляется по следующему правилу: главная диагональ определителя размером n x n последовательно заполняется коэффициентами характеристического уравнения, начиная с коэффициента при (n-1) производной до свободного члена. Столбцы вверх от главной диагонали дополняют последовательно коэффициентами с возрастающими индексами, а столбцы вниз – коэффициентами с убывающими индексами. Места, которые должны быть заняты коэффициентами с индексом выше а n и ниже а0, заполняют нулями.
Формулировка: Для того, чтобы характеристическое уравнение системы имело все корни с отрицательной вещественной частью необходимо, чтобы главный определитель Гурвица и все его диагональные миноры Dn-1, Dn-1, …, D2, D1 имели один знак с коэффициентом при старшей производной. Пример: 1. Система 1-го порядка.
2. Система 2-го порядка.
3. Система 3-го порядка.
Достоинства критерия: 1. Сравнительная простота. Недостатки: 1. Громоздкость вычислений при n>4. 2. Алгебраические критерии дают ответ на вопрос, устойчива система или нет, но ничего не говорят о том, что надо сделать, чтобы система стала устойчивой. С инженерной точки зрения более применим частотный критерий устойчивости.
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 667; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.235.210 (0.135 с.) |
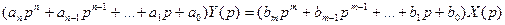
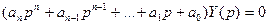
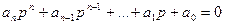 - характеристическое уравнение системы.
- характеристическое уравнение системы.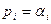 - в решении ему будет соответствовать вида
- в решении ему будет соответствовать вида 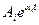 :
: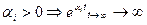 -экспонента будет неограниченно возрастать, переходный процесс расходится, система неустойчива.
-экспонента будет неограниченно возрастать, переходный процесс расходится, система неустойчива.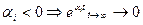 - имеем сходящийся переходный процесс, система устойчива.
- имеем сходящийся переходный процесс, система устойчива.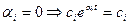 - имеем нейтрально устойчивую систему, переходного процесса нет.
- имеем нейтрально устойчивую систему, переходного процесса нет.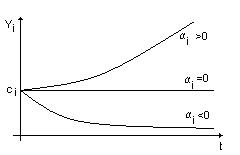
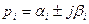
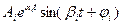
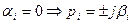
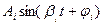 - имеем незатухающие колебания, система находится на грани устойчивости.
- имеем незатухающие колебания, система находится на грани устойчивости.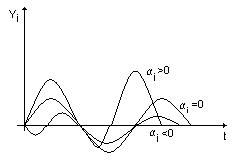
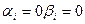
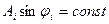 - переходного процесса нет, имеем нейтрально устойчивую систему.
- переходного процесса нет, имеем нейтрально устойчивую систему.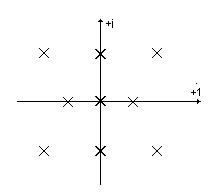
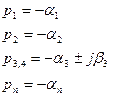 где a и b - неотрицательные числа.
где a и b - неотрицательные числа.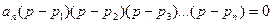
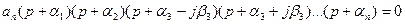
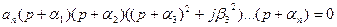
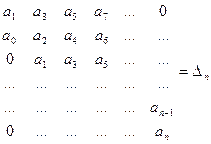
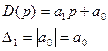 - критерий Гурвица выражается в систему двух неравенств
- критерий Гурвица выражается в систему двух неравенств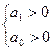
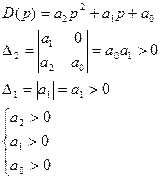
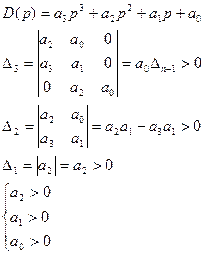
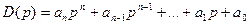
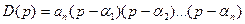
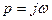 и перейдем в частотную область:
и перейдем в частотную область: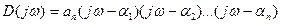
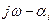 ) в виде вектора на комплексной плоскости и рассмотрим его поведение при изменении w от - ¥ до + ¥.
) в виде вектора на комплексной плоскости и рассмотрим его поведение при изменении w от - ¥ до + ¥.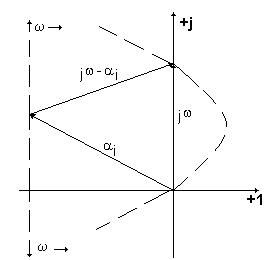

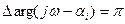 для изменения частоты w от - ¥ до + ¥.
для изменения частоты w от - ¥ до + ¥.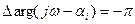
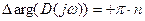
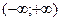
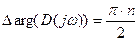
 Критерий устойчивости Михайлова
Критерий устойчивости Михайлова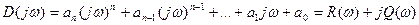 при изменении w от 0 до + ¥.
при изменении w от 0 до + ¥.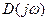 начинается на положительной вещественной полуоси
начинается на положительной вещественной полуоси 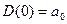 и проходит последовательно n квадрантов (где n – порядок характеристического уравнения) нигде не обращаясь в нуль, и нигде не нарушается порядок следования квадрантов.
и проходит последовательно n квадрантов (где n – порядок характеристического уравнения) нигде не обращаясь в нуль, и нигде не нарушается порядок следования квадрантов.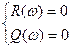
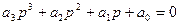 разделим на а0
разделим на а0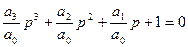 введем новую переменную
введем новую переменную 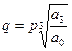
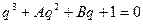 , где
, где 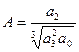
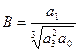
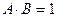
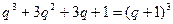 - в точке (3;3) имеем корень тройной кратности
- в точке (3;3) имеем корень тройной кратности 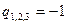
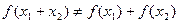
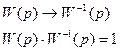 )
)