
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экономико-математические модели оптимизации.Стр 1 из 7Следующая ⇒
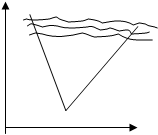
Экономико-математические модели оптимизации. Понятие оптимизационных задач и оптимизационных моделей Экономико-математические задачи, цель которых состоит в нахождении наилучшего (оптимального) с точки зрения некоторого критерия или критериев варианта использования имеющихся ресурсов (труда, капитала и пр.) называются оптимизационными. Оптимизационные задачи (ОЗ) решаются с помощью оптимизационных моделей (ОМ) методами математического программирования. Структура оптимизационных моделей состоит из целевой функции, области допустимых решений и систем ограничений, определяющих эту область. Целевая функция в самом общем виде, в свою очередь, также состоит из трех элементов: • управляемых переменных; • неуправляемых переменных; • формы функции (вида зависимости между ними). Область допустимых решений – это область, в пределах которой осуществляется выбор решений. В экономических задачах она ограничена наличными ресурсами, условиями, которые записываются в виде систем ограничений, состоящей из уравнений и неравенств. Если система ограничений несовместима, то область допустимых решений является пустой. Ограничения подразделяются: a) линейные (I и II) и нелинейные (III и IV) рис.2.1. b) детерминированные (A, B) и стохастические (Сi) рис.2.2.
Сi III
I IV В А
II х1х1
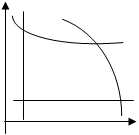
Стохастические ограничения являются возможными вероятностными и случайными. ОЗ решаются методами математического программирования, которые подразделяются на: • линейное программирование; • нелинейное программирование; • динамическое программирование; • целочисленное программирование; • выпуклое программирование; • исследование операций; • геометрическое программирование и др. Главная задача математического программирования – это нахождение экстремума функции при ограничениях в форме уравнения и неравенств. Далее будем рассматривать ОЗ, решаемые методами линейного программирования. A B
Рис. 2.3. Рис. 2.4.
Утверждение 1. Множеством решений системы m линейных неравенств с n переменными является выпуклый многогранник в n-мерном пространстве (исключая случай, когда система несовместна). Теорема 1. Множество всех допустимых решений системы ограничений задачи линейного программирования является выпуклым. Ранее говорилось, что ограничениями любой задачи линейного программирования являются либо система линейных уравнений, либо система линейных неравенств. Совокупность решений таких систем при условии их совместности образует выпуклые множества с конечным числом угловых точек. В частном случае, когда в систему ограничений - неравенств входят только две переменные x1 и x2, это множество можно изобразить на плоскости. Теорема 2. Если задача линейного программирования имеет оптимальное решение, то оно совпадает с одной (двумя) из угловых точек множества допустимых решений. Справедливость этого утверждения иллюстрируется в примере 3. Теорема 3. Каждому допустимому базисному решению задачи линейного программирования соответствует угловая точка области допустимых решений системы ограничений, и наоборот. Примеры решения заданий Пусть необходимо найти оптимальный план производства двух видов продукции Р и R, то есть такой план, при котором целевая функция (общая прибыль) была бы max, а имеющиеся ресурсы использовались бы наилучшим образом. Таблица 2.1 Данные о запасе и нормах расхода ресурсов
Требуется: I. Cформулировать экономико-математическую модель задачи в виде ОЗЛП. II. Привести ОЗЛП к канонической форме. III. Сформулировать экономико-математическую модель задачи двойственной к исходной. IV. Построить многогранник решений (область допустимых решений) и найти оптимальную производственную программу путем перебора его вершин и геометрическим способом. V. Решить задачу с помощью симплекс-таблиц. Решение: I. Оптимизационная модель задачи запишется следующим образом: а) целевая функция
б) ограничения:
в) условия неотрицательности переменных х1≥0; х2≥0. II. Приведем ОЗЛП к канонической форме. Для этого введем дополнительные переменные x 3, x 4 и x 5. а) целевая функция
б) ограничения: в) условия неотрицательности переменных III. Сформулируем экономико-математическую модель задачи двойственную к исходной. Матрица В условий прямой задачи и матрица В’ – транспонированная матрица В – имеют следующий вид:
В двойственной задаче нужно найти минимум функции Z = 12y1 + 14y2 +18y3, при ограничениях Систему ограничений-неравенств двойственной задачи обратим в систему уравнений: Компоненты у1, у2, у3 оптимального решения двойственной задачи оценивают добавочные переменные х3, х4, х5 прямой задачи. VI. Построим многогранник решений (область допустимых решений) и найдем оптимальную производственную программу путем перебора его вершин и геометрическим способом. Преобразуем нашу систему ограничений, найдя в каждом из уравнений х2 и отложим их на графике. Любая точка на данном графике с координатами х1, х2 представляет вариант искомого плана. Однако ограничения по ресурсу А сужают область допустимых решений. Ими могут быть все точки, ограниченные осями координат и прямой, так как не может быть израсходовано ресурса больше, чем его на предприятии имеется. Если точки находятся на самой прямой, то ресурс используется полностью. Аналогичные рассуждения можно привести для ресурсов В и С. В результате условиям задачи будет удовлетворять любая точка лежащая в пределах заштрихованного многоугольника. Данный многоугольник называется областью допустимых решений. Определим точки пересечения линий ограничений с осями: 1) 2) 3) Однако нам необходимо найти такую точку, в которой достигался бы max целевой функции. Оптимальную производственную программу можно найти двумя способами: 1) путем перебора его вершин Находим координаты вершин многоугольника ABCDE и подставляя в целевую функцию находим ее значение. А: А (0; 0) Z(A) =4×0+5×0=0 В: В (0; 8) Z(B) = 4×0+5×8=40 С: – это пересечение первого и второго уравнений
С (2,22; 7,55) Z(C) = 4×2,22+5×7,55=8,88+37,77=46,65
D: – это пересечение первого и третьего уравнений
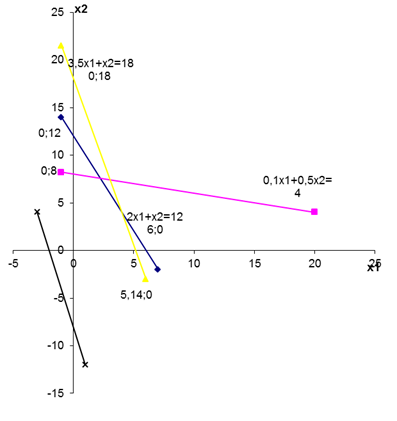
D (4; 4) Z(D)=4×4+5×4=20+25=45 E: (5,14; 0) Z(E) = 4×5,14+5×0=20,56 Находим max значение целевой функции. Оно находится в точке 2) геометрическим способом Целевая функция геометрически изображается с помощью прямой уровня, т.е. прямой на которой Z=C0+C1X1+C2X2 – принимает постоянное значение. Если С – произвольная const, то уравнение прямой имеет вид C0+C1X1+C2X2=С При изменении const С получаем различные прямые, параллельные друг другу. При увеличении С прямая уровня перемещается в направлении наискорейшего возрастания функции Z, т.е. в направлении ее градиента. Вектор градиента Точкой min Z будет точка первого касания линии уровня с допустимым многоугольником. Точкой max – точка отрыва линии уровня от допустимого многоугольника. Эти точки чаще всего совпадают с некоторыми вершинами допустимого многоугольника, хотя их может быть и бесчисленное множество, если линия уровня Z параллельна одной из сторон допустимого многоугольника. Это точка С (2,22; 7,55)
Z=46,65 у.д.е. VII. Решим задачу с помощью симплекс-таблиц. Пусть необходимо найти оптимальный план производства двух видов продукции P и R.
F(X)=4X1+5X2→max
F(X)=4X1+5X2→max Построим исходную симплекс-таблицу и найдем начальное базисное решение.
Базисное решение (0; 0; 12; 4; 18). F=0. Находим генеральный столбец и генеральную строку
Базисное решение (0; 8; 4; 0; 10). F=40.
Базисное решение (2,22; 7,56; 0; 0; 2,74). F=46,65. Эта таблица является последней, по ней читаем ответ задачи. Оптимальным будет решение (2,22; 7,56; 0; 0; 2,74), при котором Fmax =46,65, т.е. для получения наибольшей прибыли, равной 46,65 денежных единиц, предприятие должно выпустить 2,22 единиц продукции вида P и 7,56 единиц продукции вида R, при этом ресурсы A и B будут использованы полностью, а 2,74 единиц ресурса С останутся неизрасходованными.
Экономико-математические модели оптимизации.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 552; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.211.134 (0.031 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 х2х2
х2х2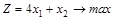
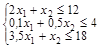
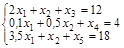
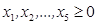 .
.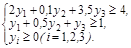
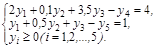
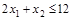 : (0;12) и (6; 0);
: (0;12) и (6; 0); : (0; 8) и (40; 0);
: (0; 8) и (40; 0);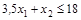 : (0; 18) и (5,14; 0);
: (0; 18) и (5,14; 0);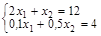 ;
; 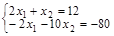 ; -9 x 2=-68 x 2=7,555; x 1=2,222.
; -9 x 2=-68 x 2=7,555; x 1=2,222.

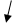






 ; 1,5 x 1=6; x 1=4; x 2=4.
; 1,5 x 1=6; x 1=4; x 2=4.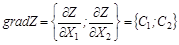
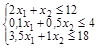
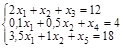
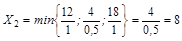 . Генеральный элемент 0,5.
. Генеральный элемент 0,5.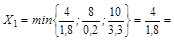 2,22222. Генеральный элемент 1,8.
2,22222. Генеральный элемент 1,8.


