
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные критерии нормальной теории и их многомерные аналоги. Информационные расстояния
Пример 6.2. { x 1,…, xn } – н.о.р. Примем за основу выборочное среднее
Если выполняется Н 0, то
Рис.6.1. Центральное и нецентральное распределения, ошибки 1-го и 2-го рода Задача 6.1. n =25, σ=2, Δ=1, α=β. Найти, чему равны α и β. Решение. Параметр нецентральности Задача 6.2. n =25, σ=1, Δ=0.5, α=0.05. Найти β. Решение. Т *= Ф-1(1- α) = 1.65. Параметр нецентральности Все задачи этого типа содержат 5 параметров. Задав любые 4 из них, можно найти значение пятого. Пример 6.3. { x 1,…, xn } – н.о.р. Статистика Т здесь, очевидно, такая же, как в примере 6.2, но неизвестное СКО приходится заменять его оценкой:
За счет дополнительного рассеяния, вызванного неопределенностью в s, центральное распределение несколько отличается от нормального. Оно называется t - распределением Стьюдента с n степенями свободы. Впрочем, при n >30 эти распределения практически неотличимы друг от друга. В статистике T дисперсию можно оценивать не относительно a 0, а относительно выборочного среднего
За счет вносимого этим дополнительного рассеяния центральным распределением статистики Т оказывается распределение Стьюдента с (n -1) степенью свободы. При известной альтернативе H 1: a = a 1 статистика Т подчиняется нецентральному распределению Стьюдента. Для векторной выборки { X 1,…, Xn }, где Xi – независимые случайные векторы, подчиняющиеся k - мерному нормальному закону N k (a, Σ) при известной ковариационной матрице Σ гипотеза H 0: a = a 0 проверяется на основе Т 2-критерия Хотеллинга:
Центральным для этой статистики является хи-квадрат (χ 2) распределение с n степенями свободы. При известной альтернативе H 1: a = a 1 статистика Т 2подчиняется нецентральному распределению хи-квадрат. При неизвестной Σ в статистику подставляется ее оценка, выборочная ковариационная матрица S = cov(X). Закон распределения статистики
даже в случае справедливости Н 0 (центральное распределение) устроен достаточно сложно. Обычно используют его аппроксимацию
где Пример 6.4. При проверке гипотезы Н 0 о равенстве средних двух независимых нормальных выборок { x 1,…, x m } и { y 1,…, yn } с известными дисперсиями σ x 2 и σ y 2 естественно использовать статистику
Ее k -мерным аналогом является двухвыборочная статистика Хотеллинга
Если значения дисперсий σ x 2 и σ y 2 неизвестны, однако известно, что между собой они равны, используется двухвыборочная статистика Стьюдента
имеющая в качестве центрального распределение Стьюдента с (m + n -2) степенями свободы. Ее k -мерным аналогом является двухвыборочная статистика Хотеллинга
Для ее центрального распределения используют аппроксимацию
При неизвестных и неравных дисперсиях задачу называют проблемой Беренса-Фишера. Оптимальный критерий здесь устроен крайне сложно. Статистику этого критерия и соответствующие таблицы можно найти в [2]. Геометрически в рассмотренных задачах границы критических областей и соответствующих доверительных областей - это поверхности эллипсоидов в Rk. Форма эллипсоидов в каждой задаче фиксирована, уровень значимости определяет величину правой части (свободного члена) в уравнении эллипсоида. Значение Т2 – статистик Хотеллинга удобно интерпретировать как расстояние в некоторой эллиптической псевдометрике - расстояние Махаланобиса DM (см. разд.5). При этом формулы (6.3-6.4) определяют квадрат расстояния Махаланобиса от
В определении расстояния Махаланобиса часто либо опускают константу перед квадратичной формой, либо, наоборот, вводят какую-нибудь специальную константу из соображений удобства для данной конкретной задачи. Замечание. Если записать для выборочной ковариационной матрицы S ее представление в виде S = ОT L О, то S -1 = ОT L-1 О так что квадратичная форма, например, в уравнении (6.3) приобретает вид
где zi – i- я главная компонента, σi2 – ее дисперсия. Таким образом, Т 2 представляет собой сумму статистик Стьюдента, построенных для каждой главной компоненты. Пример 6.5. При проверке гипотезы Н 0 о равенстве дисперсий в независимых нормальных выборках { x 1,…, x m } и { y 1,…, yn } используют статистику Фишера
в зависимости от того, как оценивались дисперсии, где F (m, n) – распределение Фишера с параметрами (степенями свободы) m, n. В многомерном анализе любой гипотезе может соответствовать большой набор видов альтернатив, поэтому там нет критериев, обладающих свойствами оптимальности. В качестве аналогов статистики F Фишера используют различные числовые характеристики матриц U = S 1 S 2-1 или V = S 1 (S 1 + S 2)-1, где S 1, S 2 - выборочные ковариационные матрицы рассматриваемых выборок. Пусть собственные числа матрицы U есть l1, …, l k, матрицы V - m1 , …, m k. Наибольшее распространение имеют следующие четыре статистики: - след Хотеллинга (или Лоули-Хотеллинга) - след Пиллаи - наибольший (наименьший) характеристический корень Роя
- статистика Уилкса Распределения этих статистик для различных нулевых гипотез устроены чрезвычайно сложно. На практике их распределения обычно аппроксимируют с помощью F -распределения со специальным выбором числа степеней свободы. Все такие статистики можно интерпретировать как меры близости в оответствующих псевдометриках. Исторически сложилось так, что их называют информационными расстояниями. Пример 6.6. Найти значения основных статистик многомерного анализа – информационных расстояний для двух 3-мерных выборкок, рассмотренных в разделе 2 и сохраненных в файле DT.mat.
|
||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 210; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.239.46 (0.018 с.) |
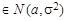 , дисперсия σ2 известна. Проверяется гипотеза H 0: a = a 0 против альтернативы H 1: a = a 1 , a 1- a 0 = Δ>0.
, дисперсия σ2 известна. Проверяется гипотеза H 0: a = a 0 против альтернативы H 1: a = a 1 , a 1- a 0 = Δ>0.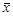 . В случае справедливости H 0
. В случае справедливости H 0 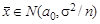 , поэтому статистику критерия Т выгодно построить так:
, поэтому статистику критерия Т выгодно построить так: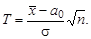 (6.1)
(6.1)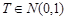 - это ее центральное распределение; если выполняется Н 1, то
- это ее центральное распределение; если выполняется Н 1, то 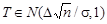 - нецентральное распределение. Величина
- нецентральное распределение. Величина 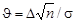 называется параметром нецентральности. Решающее правило формулируется следующим образом: выбирается критическое значение Т * (рис.12.1) и
называется параметром нецентральности. Решающее правило формулируется следующим образом: выбирается критическое значение Т * (рис.12.1) и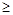 T *, то принимается Н 1.
T *, то принимается Н 1. 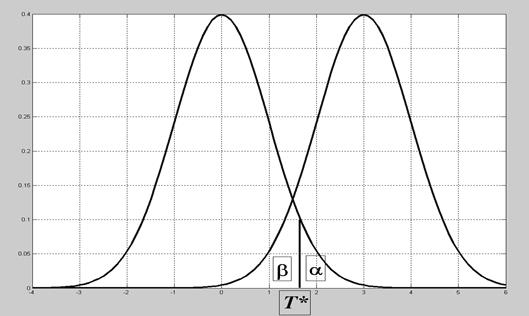
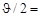 1.25. Значит, α = β = 1- Ф(1.25) = 1- 0.89 =0.11.
1.25. Значит, α = β = 1- Ф(1.25) = 1- 0.89 =0.11.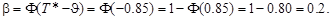
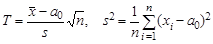 . (6.2)
. (6.2)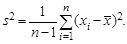
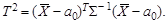 (6.3)
(6.3)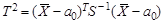 (6.4)
(6.4)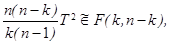 (6.5)
(6.5)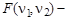 F -распределение Фишера с параметрами v 1, v 2.
F -распределение Фишера с параметрами v 1, v 2.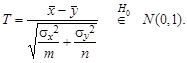 (6.6)
(6.6)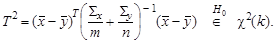 (6.7)
(6.7)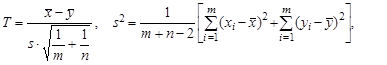 (6.8)
(6.8)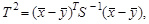 где
где 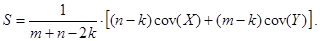 (6.9)
(6.9)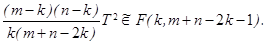 (6.10)
(6.10)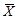 до вектора а 0, (6.7, 6.9) - квадрат расстояния Махаланобиса между
до вектора а 0, (6.7, 6.9) - квадрат расстояния Махаланобиса между 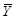 . Иногда говорят о расстоянии Махаланобиса между законами распределения. Например, расстояние между N k (a 1, å1) и N k (a 2, å2)определяется формулой
. Иногда говорят о расстоянии Махаланобиса между законами распределения. Например, расстояние между N k (a 1, å1) и N k (a 2, å2)определяется формулой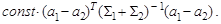
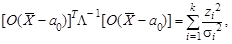
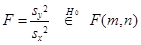 или F (m -1, n -1) (6.11)
или F (m -1, n -1) (6.11)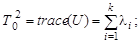
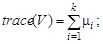
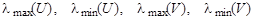 ;
;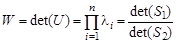 (обычно рассматривают ее логарифм).
(обычно рассматривают ее логарифм).


