
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторний добуток двох векторів ⇐ ПредыдущаяСтр 3 из 3
Векторний добуток
Геометричний зміст векторного добутку векторів Властивості векторного добутку векторів: 1. Якщо 2. 3. 4. Скалярні добутки декартових орт:
Векторні добутки декартових орт:
Змішаний (векторно-скалярний) добуток векторів Для трьох векторів
Геометрично – це є об’єм паралелепіпеда.
Властивості: 1. При циклічній перестановці векторів множників, змішаний добуток не змінюється: 2. При перестановці двох співмножників змішаний добуток змінює знак: 3. Змішаний добуток дорівнює нулю, якщо Подвійний векторний добуток Він розкривається за формулою:
Тут скалярні добутки, що позначені за допомогою круглих дужок, входять як числа.
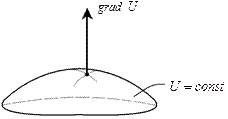
Градієнт
Нехай задано скалярне поле Очевидно, що: де Тоді визначаючи проекції градієнта U в декартовій системі координат:
Скалярне поле U породжує векторне поле
Стрілка градієнта вказує на напрямок найбільшої крутизни (рис. зліва) Градієнт ще називають просторовою похідною (рис. зверху справа).
Для наглядного відображення векторний полів переважно будують картини так званих векторних, або силових ліній. Це лінії, дотичні до яких у кожній точці вказують напрямок вектора. Густина силових ліній може відповідати інтенсивності поля. При цьому кількість силових ліній, що проходять через ортогональну площадку, повинна бути пропорційна абсолютному значенню вектора, практично постійному в межах малої площадки (див. рис., де
1.5. Потік вектора Потік вектора через поверхню S (не обов’яз-ково замкнену) – це скалярна величина, яка чисельно рівна кількості ліній вектора, що пронизують дану площадку:
Є такі типи полів векторного поля
Дивергенція Потік вектора є інтегральною характеристикою поля, яка застосовується до кінцевого об’єму, але не дає інформації про розподіл зарядів в цьому об’ємі. У зв’язку з цим вводиться аналогічна диференціальна характеристика – дивергенція вектора, яка застосовується до точки. Зменшуючи поверхню, яка обмежує деякий об’єм простору до точки, отримаємо скалярну характеристику поля – дивергенцію. Дивергенцією (а також розходженням) вектора
Дивергенція – це диференціальна операція над компонентами вектора, що приводить до скалярної величини. Якщо в деякій точці
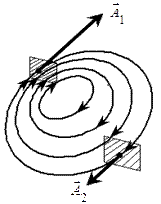
Циркуляція
Якщо крива ℓ замкнута, то лінійний інтеграл вектора Ротор Ротором (а також ротацією, вихором) вектора де Ротор – це диференціальна операція над Оператор Гамільтона Англійський математик Вільям Гамільтон помітив, що основні диференційні операції, які проводяться над скалярними і векторними полями, можна дуже зручно записати, якщо ввести особливий символ: Цей символ отримав назву “ набла ” або “ оператор Гамільтона ”. (Слово “набла” по-грецьки означає “арфа”). Основні випадки застосування набла-вектора: 1. При множенні символічно Ñ на скалярну функцію U(x,y,z) отримуємо градієнт цієї ж функції: 2. При множенні скалярно Ñ на векторну функцію F (x,y,z), отримуємо дивергенцію функції:
3. При множенні векторно набла-вектор Ñ на векторну функцію F (x,y,z), отримуємо ротор функції:
Диференціальний оператор діє тільки на той множник, який розташований безпосередньо за оператором. Приклади: 1. 2. 3. 4.
|
||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 101; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.125.171 (0.016 с.) |
 і
і  це є:
це є: 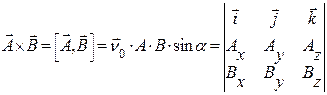 . (1.7)
. (1.7)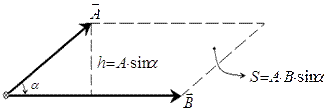
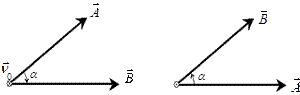 де
де  – орт, направлений по нормалі до площини векторів
– орт, направлений по нормалі до площини векторів  , відповідає переміщенню від
, відповідає переміщенню від  і
і 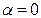 , тобто
, тобто 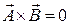 . Векторний добуток рівний нулю, коли вектори
. Векторний добуток рівний нулю, коли вектори 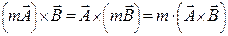 , де
, де 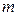 – скаляр.
– скаляр.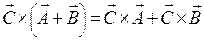 .
.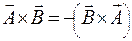 . Від перестановки множників векторний добуток змінює знак.
. Від перестановки множників векторний добуток змінює знак.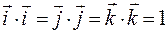
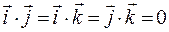 – для ^ орт.
– для ^ орт.
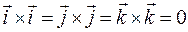
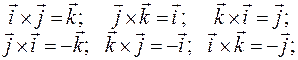
 визначено добуток:
визначено добуток: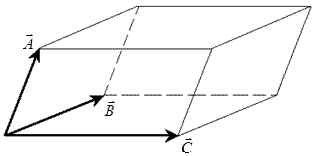
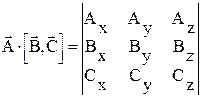 . (1.8)
. (1.8)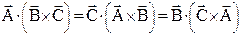 ;
;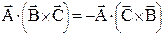 ;
; – компланарні.
– компланарні.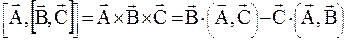 . (1.9)
. (1.9)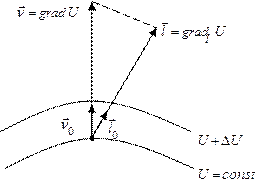

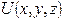 . Введемо вектор
. Введемо вектор 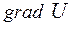 , що називається градієнтом U, який направлений у сторону максимального збільшення U і рівний швидкості зміни U у цьому напрямку (див. рис. зліва).
, що називається градієнтом U, який направлений у сторону максимального збільшення U і рівний швидкості зміни U у цьому напрямку (див. рис. зліва).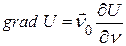 , (1.10)
, (1.10)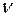 – лінія, ортогональна до поверхні рівня. І:
– лінія, ортогональна до поверхні рівня. І: 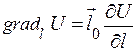 . (1.11)
. (1.11)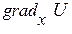 ,
, 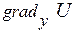 ,
, 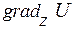 , маємо:
, маємо: 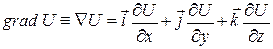 . (1.12)
. (1.12)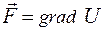 . Таке векторне поле називається потенціальним, а скалярна функція – потенціалом. Поверхні рівня, на яких
. Таке векторне поле називається потенціальним, а скалярна функція – потенціалом. Поверхні рівня, на яких 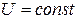 , є еквіпотенціальними поверхнями. Тоді модуль градієнта рівний:
, є еквіпотенціальними поверхнями. Тоді модуль градієнта рівний:
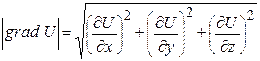 .
. 1.4. Силові лінії
1.4. Силові лінії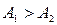 ).
).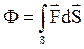 , (1.13)
, (1.13) де векторний диференціал
де векторний диференціал 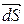 розуміється як добуток звичайного (скалярного) диференціалу поверхні
розуміється як добуток звичайного (скалярного) диференціалу поверхні 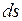 на орт нормалі
на орт нормалі 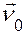 , тобто
, тобто 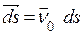 . Тому
. Тому 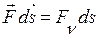 . Якщо поверхня S замкнена, то
. Якщо поверхня S замкнена, то 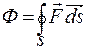 , тоді
, тоді  – орт зовнішньої нормалі, який для незамкненої поверхні вибирається довільно. Потік Ф додатній, якщо силові лінії виходять з поверхні S назовні, і від’ємний, якщо вони входять всередину (тому що, кут між
– орт зовнішньої нормалі, який для незамкненої поверхні вибирається довільно. Потік Ф додатній, якщо силові лінії виходять з поверхні S назовні, і від’ємний, якщо вони входять всередину (тому що, кут між 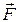 і
і 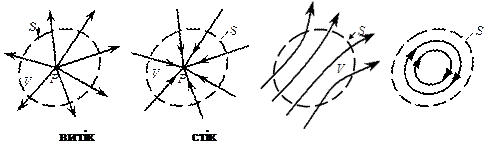
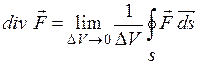 . (1.14) Дивергенція – це скалярна функція координат. Позначаючи потік вектора
. (1.14) Дивергенція – це скалярна функція координат. Позначаючи потік вектора 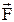 через поверхню S як D Ф, можна написати:
через поверхню S як D Ф, можна написати: 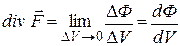 або в декартових координатах:
або в декартових координатах: 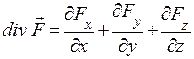 (1.15)
(1.15)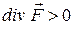 , то ця точка є джерелом силових ліній – це є витік; якщо
, то ця точка є джерелом силових ліній – це є витік; якщо 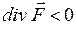 , то точка є стоком. Якщо
, то точка є стоком. Якщо 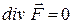 , то лінії не починаються і не закінчуються в цій точці.
, то лінії не починаються і не закінчуються в цій точці.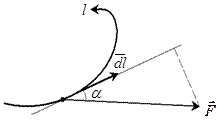 Нехай задано довільне векторне поле
Нехай задано довільне векторне поле 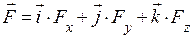 і у цьому ж полі вибрана крива l, причому вказано додатній напрямок руху по ній (див. рис.). Лінійним інтегралом вектора
і у цьому ж полі вибрана крива l, причому вказано додатній напрямок руху по ній (див. рис.). Лінійним інтегралом вектора 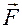 по кривій l називається криволінійний інтеграл:
по кривій l називається криволінійний інтеграл: 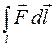 . Враховуючи, що в декартових координатах диференціал дуги рівний
. Враховуючи, що в декартових координатах диференціал дуги рівний 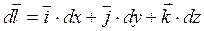 , тоді будемо мати:
, тоді будемо мати: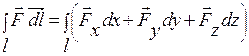
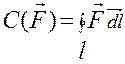 . (1.16)
. (1.16)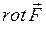 . За визначенням, проекція
. За визначенням, проекція 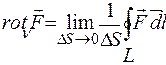 . (1.17)
. (1.17) ); L– граничний контур D S, узгоджений з
); L– граничний контур D S, узгоджений з 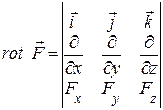
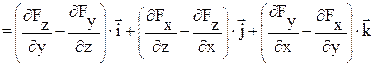 . (1.18)
. (1.18) .
.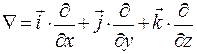 . (1.19)
. (1.19)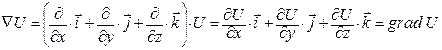
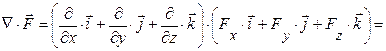
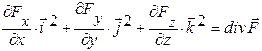
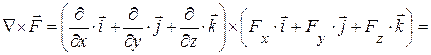
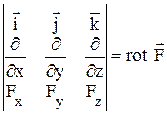
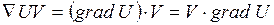 ;
;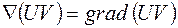 ;
;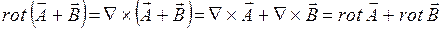 ;
;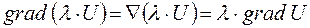 , де
, де 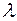 – скаляр.
– скаляр.


