Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неизвестном среднем квадратическом отклонении
До сих пор объем выборочной совокупности предполагался достаточно большим. Поэтому оценки генеральной средней считались распределенными по нормальному закону. Однако на практике часто приходится иметь дело с выборками небольшого объема (n < 20 - 30). Оказывается, что заключения, аналогичные полученным при рассмотрении выборок большого объема, возможны и в случае малых выборок, если в генеральной совокупности рассматриваемый признак распределен по нормальному закону. Пусть имеется генеральная совокупность практически неограниченно большого объема N, из которой образуется малая выборка объема n. В этом случае бесповторная выборка практически совпадает с повторной, так как величины Среднее квадратическое отклонение выборочной средней Рассмотрим случайную величину Плотность вероятностей распределения Стьюдента равна
где
В частности, при целочисленном аргументе Распределение Стьюдента определяется одним параметром Для закона распределения Стьюдента математическое ожидание и дисперсия соответственно равны:
Кривые распределения
Как видно, кривые распределения Стьюдента по форме напоминают плотность нормального распределения, но при Распределение Стьюдента играет большую роль в так называемой микростатистике (статистике малых выборок). Как известно, если плотность вероятностей ƒ(x) – четная функция, и концы интервала симметричны относительно начала координат, то
Так как функция S (t, n) четная по аргументу t, то
или
Величины
Итак, доверительный интервал Пример. Произведено 8 независимых опытов над случайной величиной X, распределенной нормально с неизвестными параметрами
Построить доверительный интервал для математического ожидания По данным опытов находим
По таблице Приложения 3 для n = 8 и γ = 0,95 находим
Следовательно, Пример. Для определения скорости автомобиля было проведено 5 испытаний, по результатам которых вычислена средняя скорость При n = 5 и
В результате
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 54; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.67.26 (0.007 с.) |
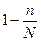 и
и 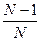 очень мало отличаются от единицы.
очень мало отличаются от единицы.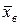 можно записать в виде
можно записать в виде 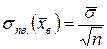 , где
, где 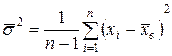 - исправленная дисперсия малой выборки.
- исправленная дисперсия малой выборки.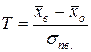 (ее возможные значения будем обозначать через t). Можно доказать, что величина T распределена по закону Стьюдента с k = n -1 степенями свободы.
(ее возможные значения будем обозначать через t). Можно доказать, что величина T распределена по закону Стьюдента с k = n -1 степенями свободы.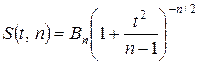 ,
,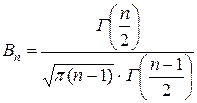 ,
, 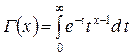 - гамма-функция.
- гамма-функция.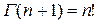
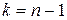 - числом степеней свободы и не зависит от неизвестных a и
- числом степеней свободы и не зависит от неизвестных a и 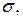 что является его большим достоинством.
что является его большим достоинством.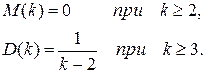
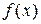 при различных значениях k показаны на рисунке.
при различных значениях k показаны на рисунке.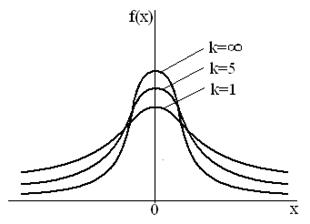
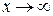 значительно медленнее приближаются к оси абсцисс. При
значительно медленнее приближаются к оси абсцисс. При 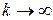 распределение Стьюдента приближается к нормальному.
распределение Стьюдента приближается к нормальному.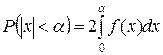 .
.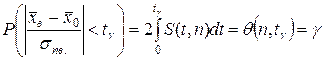
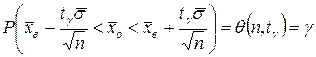 .
.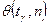 и
и 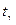 табулированы. Пользуясь таблицами распределения Стьюдента, по заданным n и γ можно найти t γ (см. Приложение 3).
табулированы. Пользуясь таблицами распределения Стьюдента, по заданным n и γ можно найти t γ (см. Приложение 3).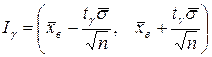 с надежностью γ накрывает неизвестное математическое ожидание
с надежностью γ накрывает неизвестное математическое ожидание 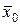 и
и 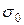 . Результаты опытов приведены ниже.
. Результаты опытов приведены ниже.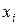
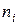
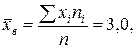
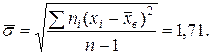
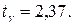 Поэтому
Поэтому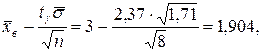
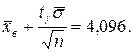
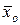 с надежностью γ = 0,95 заключено в интервале 1,904<
с надежностью γ = 0,95 заключено в интервале 1,904< 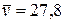 м/с. Найти 95%-ый доверительный интервал, если известно, что рассеивание скорости подчинено нормальному закону со средним квадратическим отклонением
м/с. Найти 95%-ый доверительный интервал, если известно, что рассеивание скорости подчинено нормальному закону со средним квадратическим отклонением 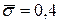 м/с.
м/с.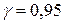 по таблице Приложения 3 находим
по таблице Приложения 3 находим 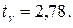 Вычисляя границы доверительного интервала, получим:
Вычисляя границы доверительного интервала, получим: