
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимальное кодирование графов
Пусть Á - некоторый класс графов, Á n , m – подмножество графов из Á, содержащих n вершин и m ребер; B ={0,1}, B * -множество слов в алфавите B. Кодированием графов из класса Á называется семейство взаимно однозначных отображений F = { j n , m: n =1,2,…; m =1,2,…;}, где j n , m: Á n , m ® B *. Слово из B *, сопоставляемое графу G Î Á n , m, называется кодом графа. Величина | j n , m (G)| - длина кода графа G Î Á n , m. При любом способе кодирования имеет место соотношение log2| Á n,m | £ max(| j n,m (G)|, G Î Á n,m ). (3.4.1) Для обоснования приведенного соотношения достаточно заметить, что если перечислить в двоичной системе счисления графы из множества Á n , m, то наибольшая длина кодов будет не менее log 2 | Á n , m |бит. Поскольку коды графов должны обеспечивать еще и возможность их однозначного восстановления, то это в общем случае потребует дополнительного увеличения длины кода. Если в соотношении (3.4.1) для любых n и m выполняется равенство, то соответствующее кодирование называется оптимальным. Если имеет место
то кодирование называется асимптотически оптимальным. Из соотношения (3.4.1) следует, что оценить качество предлагаемого кодирования графов и возможности сокращения длины кода можно, лишь подсчитав или хотя бы оценив мощность множества кодируемых при этом графов. Подсчет числа (перечисление) графов, обладающих заданными свойствами, представляет собой в общем случае довольно сложную комбинаторную задачу, требующую для своего решения полного изучения структуры перечисляемых графов. С решением этих задач можно познакомиться в [4]. Ограничимся здесь задачами перечисления помеченных графов, вершинам которых приписаны различные метки (например, номера). По всеми рассмотренным выше способам задания графов однозначно восстанавливаются именно помеченные графы, и по каждому помеченному графу однозначно строится его задание (код). Таким образом, разнообразие кодов, а, следовательно, и их наибольшая длина определяются числом различных помеченных графов. Рассмотрим степень оптимальности кодирования простых неориентированных графов с помощью матриц смежности. Подсчитаем число простых неориентированных графов, содержащих по n вершин. В полном n -вершинном графе n (n -1)/2 ребер. В каждом конкретном графе любое из этих ребер может отсутствовать или присутствовать независимо от других ребер. Поэтому число рассматриваемых графов равно числу всех подмножеств множества, содержащего n (n -1)/2 элементов, т.е. 2 n ( n -1)/2. Значение log 2 2 n ( n -1)/2 = n (n -1)/2, оносовпадает с длиной кода, формируемого по матрице смежности, позволяющего однозначно восстанавливать граф. Таким образом, кодирование простых неориентированных графов с помощью матриц смежности является оптимальным и не может быть улучшено на множестве всех таких графов. Если рассматривать не все простые неориентированные графы, а лишь некоторые подмножества, то можно сократить длину кода.
В качестве примера оптимального кодирования подмножества множества всех простых неориентированных n -вершинных графов рассмотрим класс помеченных n - вершинных деревьев. Английским математиком Кэли в середине 19 века была доказана следующая теорема. Теорема 3.4.1. Число помеченных деревьев с n ³ 2 вершинами равно nn -2. Доказательство. В задачахподсчета часто используется прием, при котором искомое множество заменяется вспомогательным, число элементов в котором устанавливается достаточно просто, а затем показывается, что исходное и вспомогательное множества равномощны. В качестве вспомогательного множества рассмотрим множество слов n - буквенного алфавита длины n -2, предложенное немецким математиком Прюфером (эти слова называют кодами Прюфера). Поскольку в каждой из n -2 позиций может стоять любая из n букв, то число таких слов равно nn -2. Установим, что вспомогательное множество равномощно искомому. Для этого покажем, что каждому помеченному дереву с n вершинами однозначно соответствует код Прюфера и наоборот. Переход от деревьев к словам Для построения кода Прюфера достаточно n -2 раза выполнить следующую процедуру: 1. Выберем в текущем (исходном) дереве висячую вершину с наименьшим номером. 2. Запишем в слово (слева-направо) номер смежной с ней вершины. 3. Удалим висячую вершину вместе с инцидентным ребром.
® 57517
Переход от слов к деревьям Запишем вспомогательный массив, содержащий числа от 1 до n и выполним n -2 раза следующую процедуру: 1. Удалим из вспомогательного массива минимальное число, которого нет в слове (исходном, а затем в текущем). 2.Удалим из текущего (исходного) слова первый элемент. 3. Составим ребро, концевыми вершинами которого являются вершины с номерами, соответствующими удаленным числам. Последнее (n -1) -ребро составляется из двух вершин с номерами, оставшимися во вспомогательном массиве после выполнения n -2 раза предыдущей процедуры. Из всех ребер получаем дерево, отождествляя вершины с одинаковыми номерами.
1 2 3 4 5 6 7 4 Для завершения доказательства необходимо показать, что граф, конструируемый из полученного списка ребер, является деревом, т.е. связен и не содержит циклов. Введем обозначения: b 1 b 2 … bn -2 - код Прюфера; a 1 – минимальное число, не входящее в b 1 b 2 … bn -2 , генерируемое ребро (a 1, b 1) a 2 – минимальное число, не входящее в b 2 b 3 … bn -2 , генерируемое ребро (a 2, b 2) ... an -2 – минимальное число, не совпадающее с bn -2 , генерируемое ребро (an -2, bn -2) (an -1, an) – последнее (n -1) - ребро. Ацикличность конструируемого графа покажем индукцией по числу ребер, перечисляя ребра в порядке обратном их генерации: 1.Граф с одним ребром (an -1, an), очевидно, не содержит циклов. 2. Предположим, что добавление к графу ребер (an -2, bn -2), …, (an - i, bn - i) не образует циклов. 3. Покажем, что добавление к графу ребра (an - i -1, bn - i -1) не сможет образовать цикл в текущем графе. Действительно, учитывая способ генерации ребер, номер an - i -1 не совпадает ни с одним из номеров bn - i -1 , bn - i, …, bn -2. Кроме того, числа ai ¹ aj при i ¹ j. Таким образом, хотя бы одна из концевых вершин добавляемого ребра (an - i -1, bn - i -1) не принадлежит уже построенному графу и цикл при этом образоваться не может. Связность графа покажем методом от противного. Пусть граф содержит k компонент связности. Каждая из них является деревом, поскольку граф не содержит циклов. При этом число вершин ni и ребер mi каждой из k компонент удовлетворяют соотношениям mi = ni -1. Просуммировав их, имеем следующие равенство Зная число помеченных n - вершинных деревьев, можно оценить степень оптимальности кода Прюфера. Пусть Tn класс всех n - вершинных деревьев. Для графов, являющихся деревьями, будем пользоваться обозначением t, учитывая (3.4.1), получаем для деревьев соотношение log 2 | T n | £ max (| j n (t)|, t Î T n). По теореме 3.4.1 имеем | Tn |= nn -2 и следовательно log 2 | T n | ³ (n -2) ë log 2 n û. Так как код Прюфера состоит из (n -2) чисел, каждое из которых принадлежит диапазону от 1 до n, то его длина | j n (t) | £ (n -2) é log 2 n ù. Объединяя оценки, имеем (n -2) ë log 2 n û £ log 2 | T n | £ max (| j n (t)|, t Î T n) £ (n -2) é log 2 n ù.
При этом предел (3.4.2) равен единице
Следовательно, рассмотренное кодирование помеченных деревьев является асимптотически оптимальным. На подпоследовательности n =2 i, i =1,2,… кодирование является оптимальным.
|
|||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 124; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.174.195 (0.017 с.) |
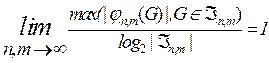 , (3.4.2)
, (3.4.2)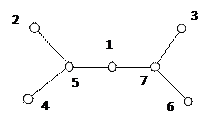 Пример 3.4.1.Помеченное 7- вершинное дерево и его код Прюфера
Пример 3.4.1.Помеченное 7- вершинное дерево и его код Прюфера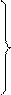 Пример 3.4.2.Код Прюфера и восстановленное по нему дерево.
Пример 3.4.2.Код Прюфера и восстановленное по нему дерево.
 73442 6
73442 6 n =7 (1,7)(3,5)(3,4)(4,6)(2,4)(2,7) 5 3 2 7 1
n =7 (1,7)(3,5)(3,4)(4,6)(2,4)(2,7) 5 3 2 7 1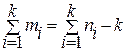 , где
, где 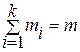 и
и 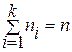 . Таким образом, получаем, что
. Таким образом, получаем, что 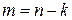 . Но в построенном графе
. Но в построенном графе 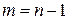 . Следовательно,
. Следовательно, 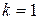 и граф содержит лишь одну компоненту связности. ð
и граф содержит лишь одну компоненту связности. ð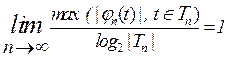 .
.


