Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эйлеровы и гамильтоновы графы
При решении задачи о кёнигсбергских мостах Л.Эйлер сопоставил каждой части суши, включая и острова, вершину, а каждому мосту - ребро, соединяющее соответствующую пару вершин. Получился следующий граф:
Решение исходной задачи эквивалентно нахождению в этом графе цикла, содержащего все его рёбра. Нетрудно убедиться (перебором), что для данного графа не существует искомого цикла. Л.Эйлер ответил на вопрос, когда в произвольном связном графе G (V, E) можно выделить цикл, содержащий все его рёбра. Такие графы и циклы называются для краткости эйлеровыми. Теорема 1.3. 1. Связный граф G является эйлеровым тогда и только тогда, когда каждая вершина в G имеет чётную степень. Доказательство. Необходимость очевидна, так как при каждом прохождении через вершину используется по два ребра. Достаточность покажем индукцией по M -числу рёбер в графе G:
M =2: Утверждение теоремы верно. 2. Предположим, что теорема верна и для M =3,4, …, m. 3. Рассмотрим произвольный граф с m +1 ребром, все вершины которого имеют чётные степени. Покажем сначала, что в таком графе найдется хоть какой-то цикл. Действительно, если это не так, то тогда каждое ребро графа является мостом. Структура графа относительно произвольного ребра-моста (vi, vj) указана ниже на левом рисунке. Удалим ребро (vi, vj), склеив компоненты связности по вершинам vi и vj. Обозначим новую вершину через v 0. При этом получим граф, указанный справа на рис. 1.3.1.
vi vj v 0 Рисунок.1.3.1. В построенном графе m рёбер. Вершина v 0 имеет чётную степень, равную сумме двух нечетных чисел; степени всех остальных вершин сохранили свою четность. Следовательно, по предположению индукции в полученном графе существует эйлеров цикл и ни одно его ребро не является мостом, что противоречит предположению о том, что все рёбра исходного являются мостами. Следовательно, хотя бы один цикл в графе G найдется. Если цикл содержит все рёбра графа, то теорема доказана.
Если цикл не содержит всех рёбер, рассмотрим подграф Из доказательства нетрудно получить Следствие 1.3.1. Связный граф G является эйлеровым тогда и только тогда, когда множество его рёбер можно разбить на порёберно непересекающиеся циклы, причём процесс разбиения всегда можно довести до простых циклов. Цепь, содержащую все ребра графа, называют эйлеровой цепью, а соответствующий граф – полуэйлеровым. Следствие 1.3.2. Связный граф G содержит эйлерову цепь (является полуэйлеровым) тогда и только тогда, когда в графе G две вершины нечётной степени. Для построения эйлеровой цепи достаточно выделить в графе G некоторую цепь, соединяющую вершины нечётной степени. Если эта цепь содержит все ребра графа G, то задача решена. В противном случае рассмотрим подграф Решая задачу о Кенигсбергских мостах, Эйлер показал, что число вершин нечётной степени в любом графе всегда чётное число (попробуйте доказать этот факт самостоятельно). Приложения эйлеровых графов связаны с построением изображений. Они встречаются, как в занимательных задачах: можно ли нарисовать какую-либо фигуру, не отрывая карандаш от бумаги (начиная и заканчивая в одной и той же точке, в разных точках и т.п.), так и в задачах, связанных с повышением производительности таких периферийных устройств компьютера, как графопостроители, плоттеры и т.д.
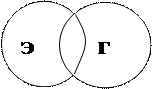
Для ориентированных эйлеровых графов справедлива следующая теорема. Теорема 1. 3. 2. Связный ориентированный граф D является эйлеровым тогда и только тогда, когда для каждой вершины графа D выполняется равенство полустепеней захода и исхода. Доказательство проводитсяаналогично неориентированному случаю. ð Гамильтоновы графы Если в рассмотренной выше задаче заменить слово «ребро» на слово «вершина», то приходим к изучению графов, в которых можно выделить цикл, содержащий все вершины. В отличие от эйлеровых графов описание класса таких графов оказалось существенно более сложной задачей. Одним из первых исследователей этой задачи был лорд Гамильтон. Графы, в которых можно выделить цикл, содержащий все вершины, называются поэтому гамильтоновыми. Классы эйлеровых и гамильтоновых графов имеют пересечение, но ни один из них не содержится в другом:
В качестве примеров графов, являющихся одновременно эйлеровыми и гамильтоновыми, можно привести простые циклы Cn, n =1,2,…. Два простых цикла с общей вершиной образуют эйлеров, но не гамильтонов граф. Два простых цикла с общим ребром образуют гамильтонов граф, не являющийся эйлеровым. Одной из характерных особенностей дискретной математики и теории графов, в частности, является возможность существенного изменения сложности решения задачи даже при небольшом её изменении. Постановка задачи о гамильтоновых графах отличается от задачи эйлеровых графов, как уже указывалось, заменой слова «ребро» на слово «вершина». Однако, сложность задачи при этом значительно возросла. До сих пор нет характеризации класса гамильтоновых графов, то есть не найдены необходимое и достаточное условие гамильтоновости графа, хотя с со времени постановки задачи прошло уже больше 150 лет. Удалось лишь сформулировать и доказать некоторое количество достаточных условий гамильтоновости. Очевидно, что полные графы являются гамильтоновыми. Если рассмотреть процесс удаления ребер из полного графа, то его остовный подграф на некотором этапе станет негамильтоновым. Информацию о границах этого перехода содержит следующая теорема.. Теорема 1. 3.3. Если в графе G (V, E), | V | = n, степень каждой вершины не меньше n /2, то граф G гамильтонов. Доказательство этой теоремы можно найти в [3]. ð
|
|||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 237; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.86.138 (0.007 с.) |


 1. M =1: . Утверждение справедливо(вклад петли в степень равен 2)
1. M =1: . Утверждение справедливо(вклад петли в степень равен 2)

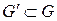 , порожденный рёбрами, не вошедшими в цикл. Подграф
, порожденный рёбрами, не вошедшими в цикл. Подграф 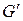 может состоять из одной или нескольких компонент связности, в каждой из которых степени всех вершин чётны, а число рёбер не больше m. По предположению индукции, в каждой такой компоненте существует эйлеров цикл. Объединив эти циклы с первоначально выделенным циклом (они попарно пореберно не пересекаются), получаем эйлеров цикл всего графа G. ð
может состоять из одной или нескольких компонент связности, в каждой из которых степени всех вершин чётны, а число рёбер не больше m. По предположению индукции, в каждой такой компоненте существует эйлеров цикл. Объединив эти циклы с первоначально выделенным циклом (они попарно пореберно не пересекаются), получаем эйлеров цикл всего графа G. ð