
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кумулятивные ряды распределения
Кумулятивный ряд распределения — это ряд распределения, в котором вместо ряда частот записывается ряд накопленных частот. Кумулятивный ряд можно строить для дискретного и для непрерывного признака. Строится он с помощью соответствующего ряда распределения. Пусть имеется дискретный ряд распределения примера п. 4.2.
Для вычисления накопленных частот в таблице добавляется новая строка "Накопленные частоты", в которой слева направо последовательно выписываются накопленные частоты. Накопленная частота для варианты равна сумме частоты этого варианта и всех частот в таблице слева от нее.
В итоге имеем
или, окончательно,
Аналогично строится кумулятивный ряд распределения для непрерывных признаков. Приведем следующий пример.
или
Графическое изображение рядов распределения Полигон распределения Полигоном распределения (полигоном) называют диаграмму для изображения дискретного вариационного ряда. Пусть имеется дискретный ряд распределения
На плоскости строится прямоугольная система координат. На горизонтальной оси отмечаются точки — варианты. Слева и справа от крайних вариантов отмечают еще по одной точке, как бы еще по одному варианту с частотой, равной 0. В каждой такой точке восстанавливается перпендикуляр, длина которого равна частоте варианта. Концы перпендикуляров, начиная с левого фиктивного варианта, последовательно соединяют отрезками прямых (см. рис. 2). Это и есть полигон для рассматриваемого признака. Полигон, в переводе с греческого, — многоугольник. Другое название — экспериментальная кривая распределения частот. Рис. 2
5.2. Гистограмма (столбиковая диаграмма) Гистограммы (столбиковые диаграммы) используются для изображения интервальных вариационных рядов. Пусть дан интервальный ряд распределения из п. 4.3.
На плоскости строится прямоугольная система координат. На горизонтальной оси отмечаются точки, концы интервалов ряда. На каждом интервале, как на основании, строится прямоугольник, высота которого равна частоте признака (рис. 3). Результатом построения и является гистограмма. Рис. 3 Кумулята Кумулятой называют диаграмму для изображения кумулятивного ряда. Для дискретного признака кумулята строится с помощью кумулятивного ряда распределения. На горизонтальной оси добавляют только один левый фиктивный вариант с частотой, равной 0. Для кумулятивного дискретного ряда п. 4.4 кумулята будет выглядеть, как представлено на рис. 4.
Рис. 4 При построении кумуляты для интервального ряда распределения, его заменяют дискретным (за вариант берется середина интервала) и построения делают, как в предыдущем случае. Для кумулятивного ряда распределения
кумулятивный дискретный ряд будет иметь вид
Построенная кумулята изображена на рис. 5. Рис. 5 6. Показатели центра распределения Основные понятия Любой многоэлементный объект человек обычно оценивает небольшим числом параметров. Для описания центра в физике известно понятие центра тяжести (центра масс), в геометрии — центра симметрии. Для описания центра статистического явления используется понятие центра распределения. Традиционно в статистике используют следующие показатели центра распределения: мода, медиана, среднее арифметическое. Мода Мода — это значение признака, которое в выборке имеет наибольшую частоту, обозначается Mo. Для дискретного признака мода вычисляется очень легко. Например, для дискретного ряда распределения
В данном случае наибольшую частоту имеет варианта 21. Следовательно, Mo =21. Если дискретный ряд распределения представлен в виде полигона, то мода — это варианта, в которой график имеет вершину. Дискретный признак может иметь одну моду, тогда он называется унимодальным, иметь две моды (две вершины полигона), тогда он называется бимодальным. Признак может вообще не иметь моды (более двух значений имеют одинаковую наибольшую частоту). Если признак непрерывный, то мода вычисляется следующим образом. Пусть дан непрерывный признак с интервальным рядом распределения
Пусть x1 — начало интервала с наибольшей частотой fM. Частота на предыдущем интервале f (–), на последующем — f (+). Мода вычисляется по формуле
В нашем случае имеем Медиана Медиана — это число, которое на числовой оси делит все измеряемые значения признака на две равные по количеству группы: одни наблюдения не больше этого числа, другие — не меньше. Обозначается Me. Для дискретных признаков медиана находится по следующим правилам. Все наблюдения (с повторениями значений, если они есть) выстраивают в порядке возрастания. Находится число (n +1)/2. Если объем выборки n число нечетное, то это число конкретное и является номером члена в упорядоченной выборке. Например: 2, 5, 6, 6, 8, 10, 13, 14, 16, то п = 9 и (п + 1)/2 = 5. Медианой будет пятое значение в этом ряду (подчеркнуто): Me = 8. Если объем выборки число четное, то (n +1)/2 — дробное число. За медиану берут полусумму двух соседних значений. Например: 3, 5, 5, 7, 10, 11, 15, 17; п = 8 и (п + 1)/2 = 4,5. Медиана есть полусумма четвертого и пятого значений (подчеркнуты): Me = (7 + 10)/2 = 8,5. Повторения в ряду наблюдений могут попасть в середину упорядоченной выборки. Это правил подсчета не меняет. Например, 1, 2, 4, 4, 4, 7, 9; n = 7; в данном случае Me = 4. Если имеем выборку вида 3, 5, 8, 8, 8, 10, 11, 15; здесь п = 8, Me = 8. В примере п. 4.2 M e = 21. Для непрерывных признаков медиана вычисляется с помощью интервального и кумулятивного рядов. Пусть дан интервальный ряд распределения и одновременно построен кумулятивный:
Пусть x 1 — начало, а x 2 — конец интервала с частотой fM е, на котором находится медиана. До интервала накоплена частота f (–). Будем искать медиану по формуле
Объем выборки n = 60 — число четное, (n +1)/2 = 30,5. По правилам для дискретных признаков надо искать полусумму 30-го и 31-го значений в упорядоченном ряду наблюдений. Эти значения находятся на интервале (8,5; 9,5), так как по кумулятивному ряду до этого интервала накопленная частота равна 15 (< 30,5), а вместе с интервалом — 38 (> 30,5). Тогда x 1 = 8,5; x 2 = 9,5; fM е, = 23; f (–) = 15. Используя формулу выше, получим M e = 8,5 + (30,5 – 15) (9,5 – 8,5)/23 = 8,5 + 15,5/23» 9,174.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 1544; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.0.192 (0.014 с.) |
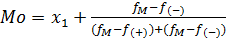 .
.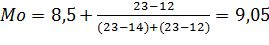 .
. .
.


