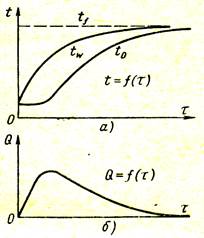Теплопроводность однослойной плоской  

                                             СТЕНКИ

  Рассмотрим температурное поле и тепловой поток при стационарной теплопроводности  через однослойную плоскую стенку, площадь боковой поверхности которой настолько велика, что теплообменом через ее торцы можно пренебречь. Участок такой стенки изображен на рис. 2.4. Стенка имеет толщину δ и одинаковый для всей стенки коэффициент теплопроводности λ. Температуры на границах стенки Т_с1  и Т_с2 поддерживаются постоянными, а изотермические поверхности имеют форму плоскостей, параллельных поверхностям стенки. Температура меняется только в направлении, перпендикулярном к плоскости стенки, которое принимаем за ось x. При рассматриваемых условиях теплота может распространяться только вдоль оси x, и температурное поле будет одномерным. Температурные градиенты вдоль остальных осей координат равны нулю:

 

            ∂Т/∂y =  ∂Т/∂z = 0  и   ∂²Т/∂y² =  ∂²Т/∂z² = 0.     (2.16)

 

  Поэтому дифференциальное уравнение теплопроводности (2.14) приводится к виду:

                                             d²Т/dx²  = 0.                                      (2.17)

 

Проинтегрировав это уравнение дважды, найдем:     

                                           

                                            dТ/dx  = С₁,                                       (2.18)

  

                                       Т = С₁x + С₂,                                           (2.19)

 

 где С₁ и С₂ – постоянные интегрирования.

 

            Рис.2.4. Изменение температуры по толщине

                              однослойной плоской стенки

 

Следовательно, температурное поле однослойной плоской стенки при постоянном коэффициенте теплопроводности выражается линейной зависимостью температуры от координаты (рис. 2.4).

Для определения постоянных интегрирования С₁ и С₂ воспользуемся граничными условиями первого рода, т.е. зададимся законом распределения температур на поверхности тела для любого момента времени:

                                   при x = 0 Т = Т_с1;

 

                                   при x = δ Т = Т_с2.

  

Подстановка этих условий в уравнение (2.19), дает:

 

                                С₂ = Т_с1; С₁ = (Т_с2 – Т_с1)/δ.                         (2.20)

    Заменив в (2.19) постоянные интегрирования найденными выражениями (2.20), получим уравнение стационарного температурного поля однослойной плоской стенки:

 

                                     Т = (Т_{с2 –} Т_с1)∙_·x/δ + Т₁.                             (2.21)

 

Определим плотность теплового потока через плоскую стенку. В соответствии с законом Фурье с учетом равенства (2.18) можно записать:

 

                         q = - λ∙_·∂Т/∂x = - λС₁ = - λ∙(Т_с2 – Т_с1)/δ.             (2.22)

 

Или

                                        q = λ∙(Т_с1 – Т_с2)/δ.                                (2.23)

 

Зная плотность теплового потока через плоскую стенку, можно вычислить общее количество теплоты, которое передается через поверхность стенки F:

 

                                        Q = λF∙(Т_с1 – Т_с2)/δ.                                (2.24)

 

 Следовательно, количество теплоты, передаваемое теплопроводностью через однослойную плоскую стенку, прямо пропорционально коэффи-циенту теплопроводности стенки, её площади, разности температур на-ружных поверхностей стенки и обратно пропорционально толщине стенки.

Соотношение λ/δ называется тепловой проводимостью плоской стенки, а обратная величина δ/λ – термическим сопротивлением плоской стенки.

 

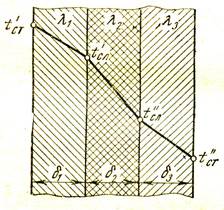
  2.2.2. ТЕПЛОПРОВОДНОСТЬ МНОГОСЛОЙНОЙ ПЛОСКОЙ

                                              СТЕНКИ                                

В тепловых аппаратах часто встречаются стенки, состоящие из нескольких плоских слоев различных материалов. Оценим темпе-ратурное поле и тепловой поток теплопроводностью через многослой-ную плоскую стенку, полагая, что все слои плотно прилегают друг к другу.

При стационарном тепловом режиме тепловые потоки через каждый из слоев будут одинаковыми, так как только при этом условии темпера-турное поле не изменяется с течением времени.

Для решения этой задачи рассмотрим трехслойную стенку, в которой толщина отдельных слоев равна δ₁, δ₂, δ₃, а их коэффициенты тепло-проводности соответственно λ₁, λ₂, λ₃ (рис. 2.5). На внешних поверх-ностях стенки поддерживаются постоянные температуры Т_с1 и Т_с2, причем Т_{с1 >} Т_с2; температуры на границах между слоями Т_сл1 и Т_сл2.

 

                 Рис. 2.5. Изменение температуры по толщине

                                 многослойной плоской стенки

 

Выразим плотности тепловых потоков через отдельные слои с помощью формулы (2.23):

                                           q = λ₁∙(Т_с1 – Т_сл1)/δ₁,

 

                                           q = λ₂∙(Т_сл1 – Т_сл2)/δ₂,                        (2.25)

                                               

                                           q = λ₃∙(Т_сл2 – Т_с2)/δ₃.

 

Перепишем эти уравнения в виде:

 

                                             (Т_с1 – Т_сл1) = qδ₁/λ₁,

                                

                                             (Т_сл1 – Т_сл2) = qδ₂/λ₂,                       (2.26)

                                           

                                             (Т_сл2 – Т_с2) = qδ₃/λ₃.

 

 Просуммировав правые и левые части этих равенств, получим:

                                                                                          

                               Т_с1 – Т_с2 = q(δ₁/λ₁ + δ₂/λ₂ + δ₃/λ₃).                                                                                   

 

Откуда                  q = (Т_с1 – Т_с2)/(δ₁/λ₁ + δ₂/λ₂ + δ₃/λ₃).              (2.27)

 

Или для любой плоской многослойной стенки, состоящей из n слоев

                                                              _{i =n}

                                    q = (Т_с1 – Т_с2) / ∑ δ_i/λ_i,                         (2.28)

                                                              ^{i =1}

Здесь i – номер слоя.

        _{i = n}

Величина ∑ δ_i/λ_i называется полным термическим сопротивлением                            

              ^{i = 1}

многослойной плоской стенки.    

Зная плотность теплового потока через многослойную плоскую стенку, можно вычислить общее количество теплоты, которое переда-ется через наружную поверхность стенки F:

                                                              _{i =n}

                                 Q = F∙(Т_с1 – Т_с2) / ∑ δ_i/λ_i,                        (2.29)

                                                              ^{i =1}

Для построения температурного поля многослойной стенки необходимо оценить температуру на поверхности каждого слоя в отдельности. Система уравнений (2.26) позволяет получить расчетные формулы для определения температуры на поверхности любого слоя:

 

                                        Т_сл1 = Т_с1 - qδ₁/λ₁,

 

                                        Т_сл2 = Т_сл1 - qδ₂/λ₂,                                (2.30)

                                            

                                        Т_с2  = Т_сл2 - qδ₃/λ₃.

 

Температура в каждом слое стенки при постоянном для слоя коэффициенте теплопроводности изменяется по линейному закону, а для многослойной плоской стенки в целом она представляет собой ломаную линию. Температурное поле многослойной стенки изображено на рис. 2.5. Наклон температурной линии в отдельных слоях различен. Это объясняется тем, что плотность теплового потока через каждый из слоев будет одинаковой:

 

                                       q = - λ∙_·∂Т/∂x = const. 

 

 Поэтому слои с меньшим коэффициентом теплопроводности имеют больший температурный градиент ∂Т/∂x и, следовательно, больший наклон температурной линии.

  При выводе формул для температурного поля и теплового потока теплопроводностью через многослойную плоскую стенку мы предполагали, что все слои плотно прилегают один к другому и благодаря хорошему контакту соприкасающиеся поверхности разных слоев имеют одну и ту же температуру. В действительности на границе раздела двух слоев зачастую имеет место неплотное соприкосновение поверхностей. Это приводит к возникновению контактного термичес-кого сопротивления. В результате уменьшается тепловой поток тепло-проводностью через многослойную стенку.

Повышение сопротивления тепловому потоку в месте контакта двух поверхностей обусловлено меньшим коэффициентом теплопроводности газовой прослойки по сравнению с твердым телом, отклонением направления теплового потока от нормали к поверхности контакта, повышенным термическим сопротивлением поверхностного слоя из-за окисной пленки и загрязения. Надежные сведения о величинах контактного термического сопротивления получаются опытным путем.

Контактное термическое сопротивление существенно уменьшается при покрытии соприкасающихся поверхностей мягкими металлами (медь, олово и др.) или при прокладках из мягких материалов.

    

 

      2.2.3. ТЕПЛОПРОВОДНОСТЬ ОДНОСЛОЙНОЙ

                             ЦИЛИНДРИЧЕС КОЙ СТЕНКИ

  Рассмотрим теплопроводность однородной цилиндрической стенки большой длины так, чтобы передачей теплоты с торцов трубы можно было пренебречь (рис. 2.6). Если внутренняя и внешняя поверхности поддерживаются при постоянных температурах Т_с1 и Т_с2, то тепловой поток имеет радиальное направление, а изотермические поверхности имеют форму цилиндров, у которых общая ось с трубой. В этих услови-ях температурное поле будет одномерным:

 

                                             Т = f (r),

 

где r – текущая цилиндрическая координата.

На рис. 2.6 изображена цилиндрическая стенка длиной l, у которой внутренний радиус равен r₁, а наружный - r₂. Коэффициент теплопро-водности λ будем считать одинаковым для всей стенки.

 

 

Рис. 2.6. Изменение температуры по толщине однослойной         

                                     цилиндрической стенки

 

Для стационарной одномерной задачи о теплопроводности цилиндрической стенки без внутренних источников теплоты дифферен-циальное уравнение теплопроводности (2.15) приводится к виду:

 

                                   d²Т/dr²  + 1/r ∙_·dТ/dr = 0.                           (2.31)

 

Введение новой переменной u = _·∂Т/∂ r позволяет привести уравнение (2.31) к виду:

                                            du/d r + u/r = 0.                               (2.32)

Разделим переменные                                    

                                            du/u + d r/r = 0                                (2.33)

и проинтегрируем                                              

                                           ln u + ln r = ln С₁.                                                     (2.34)

 

 Потенцирование этого выражения ur = С₁, переход к первоначальным

координатам    

                         dТ/d r ∙ r = С₁   или dТ = С₁ ∙ d r/r

 

и интегрирование дает

                                             Т = С₁ ln r + С₂,                               (2.35)

 

где С₁ и С₂ – постоянные интегрирования.

Следовательно, распределение температур в стенке цилиндрической трубы представляет собой логарифмическую кривую.

Искривление линии температурного поля в цилиндрической стенке обусловлено изменением плотности теплового потока при изменении радиуса цилиндра: при уменьшении радиуса площадь поверхности, через которую проходит тепло, также уменьшается. Поэтому на малых радиусах температурная линия проходит более круто. Это правило остается в силе и при обратном направлении теплового потока (пунктир на рис. 2.6).

     Для определения постоянных интегрирования С₁ и С₂ воспользуемся граничными условиями первого рода, т.е. зададимся законом распределения температур на наружной и внутренней поверх-ности цилиндрической стенки для любого момента времени:

 

                                   при r = r₁ Т = Т_с1;

 

                                   при r = r₂ Т = Т_с2.

  

Подставив эти эти выражения в уравнение (2.35), получим:

 

    С₁ = (Т_с1–Т_с2)/ln (r₁/r₂); С₂ = Т_{с1 –} (Т_с1–Т_с2)∙ln r₁/ln (r₁/r₂).    (2.36)        

                                                                                                                                  

Заменив в (2.35) постоянные интегрирования найденными выражениями (2.36), получим уравнение стационарного температурного поля однородной цилиндрической стенки:

 

                           Т = Т₁ - (Т_{с1 –} Т_с2)∙ln (r/r₁) / ln (r₂/r₁),                  (2.37)

 

где r – переменный радиус.

Определим тепловой поток через изотермическую поверхность с радиусом r. В соответствии с законом Фурье:

 

                                Q = - λF_·dТ/dr = - λ2πr l ∙_·dТ/dr.                      (2.38)

 

Из формулы (2.37) в результате вычисления производной от Т по переменному радиусу r получается следующее выражение для температурного градиента:

 

                                 dТ/dr = - (Т_{с1 –} Т_с2)∙(1/r) / ln (r₂/r₁).              (2.39)

 

После подстановки выражения (3.39) в (3.38) получим формулу для теплового потока:

 

  Q = πl(Т_с1 – Т_с2) / (1/2λ) ln (r₂/r₁) =πl(Т_с1 – Т_с2) / (1/2λ) ln (d₂/d₁). (2.40)

 

Если отнести тепловой поток к единице длины цилиндрической стенки, то формула (2.40) перепишется в виде:

 

       q _l = π(Т_с1–Т_с2)/(1/2λ)ln (r₂/r₁) = π(Т_с1 – Т_с2)/(1/2λ) ln (d₂/d₁). (2.41)

 

Величину (1/2λ) ln (d₂/d₁) называют термическим сопротивлением цилиндрической стенки.

Обозначим плотности теплового потока на внутренней и внешней поверхностях через q₁ и q₂. Так как

 

                                   Q = q _l l = q₁ 2πr₁ l = q₂ 2πr₂ l,

то

                                       q _l = q₁ 2πr₁  = q₂ 2πr₂ .                          (2.42)

 

Отсюда плотность теплового потока:

 на внутренней поверхности цилиндрической стенки

 

                          q₁  = q _l / 2πr₁ = (Т_с1 – Т_с2) / (r₁/λ)ln (r₂/r₁),           (2.43)

 

на внешней поверхности цилиндрической стенки

 

                       q₂  = q _l / 2πr₂ = (Т_с1 – Т_с2) / (r₂/λ)ln (r₂/r₁).              (2.44)

 

Если r₂/r₁ < 2, т.е. труба тонкостенная, то кривизна стенки слабо влияет на величину теплового потока. В этом случае (с точностью до 4%) для определения теплового потока, отнесенного к единице длины цилиндрической стенки, вместо выражения (2.41) можно использовать формулу плоской стенки:

 

                               q _l = 2 λ π r_cр(Т_с1 – Т_с2) / (r₂  - r₁),                     (2.45)

 

где r_cр – средний радиус цилиндрической стенки.

 

 

                                 

2.2.3. ТЕПЛОПРОВОДНОСТЬ МНОГОСЛОЙНОЙ

                            ЦИЛИНДРИЧЕС КОЙ СТЕНКИ

   Как и в случае с плоской многослойной стенкой, в тепловых аппаратах также часто встречаются стенки, состоящие из нескольких цилиндрических слоев различных материалов. Оценим температурное поле и тепловой поток теплопроводностью через многослойную цилиндрическую стенку стенку, полагая, что все слои плотно прилегают друг к другу.

  Для решения этой задачи рассмотрим трехслойную цилиндрическую стенку, в которой радиусы слоев r₁, r₂, r₃, r₄, а их коэффициенты теплопроводности соответственно λ₁, λ₂, λ₃ (рис. 2.7). На внешних поверхностях стенки поддерживаются постоянные темпе-ратуры Т_с1 и Т_с2, причем Т_{с1 >} Т_с2; температуры на границах между слоями Т_сл1 и Т_сл2. Температура каждого слоя стенки изменяется по логарифмической кривой. Общая температурная кривая представляет собой ломаную логарифмическую кривую.

При стационарном тепловом режиме тепловые потоки через каждый из слоев будут одинаковыми, так как только при этом условии температурное поле не изменяется с течением времени.

Выразим тепловой поток, отнесенный к единице длины цилиндри-

ческой стенки, через отдельные слои с помощью формулы (2.41):

 

                                q _l = π(Т_с1 – Т_сл1) / (1/2λ₁)ln (r₂/r₁), 

                     

                                  q _l = π(Т_сл1 – Т_сл2) / (1/2λ₂)ln (r₃/r₂),                (2.46)       

                                

                                q _l = π(Т_сл2 – Т_с2) / (1/2λ₃)ln (r₄/r₃).                      

 

 

    Рис. 2.7. Изменение температуры по толщине многослойной              

                                     цилиндрической стенки

 

Перепишем эти уравнения в виде:

 

                                    (Т_с1 – Т_сл1) = q _l (1/2πλ₁)ln (r₂/r₁),

                                 

                                    (Т_сл1 – Т_сл2) =q _l (1/2πλ₂)ln (r₃/r₂),              (2.47)

                                   

                                    (Т_сл2 – Т_с2) = q _l (1/2πλ3)ln (r4/r3).

 

 Просуммировав правые и левые части этих равенств, получим:

                                                                                              

   Т_с1 – Т_с2 = q _l [(1/2πλ₁)ln (r₂/r₁) + (1/2πλ₂)ln (r₃/r₂) + (1/2πλ₃)ln (r₄/r₃)].                                                                               

 

Откуда 

 

q _l = π(Т_с1 – Т_с2) /[(1/2λ₁)ln (r₂/r₁) + (1/2λ₂)ln (r₃/r₂) + (1/2λ₃)ln (r₄/r₃)]. (2.48)       

 

Или для любой цилиндрической многослойной стенки, состоящей из n слоев                                                _n

                             q _l = π(Т_с1 – Т_с2) / ∑(1/2λ_i)∙ln (r_i+1/ r_i).             (2.49)

                                                         ⁱ⁼¹

 Здесь i – номер слоя.

               _{i = n}

Величина ∑ (1/λ_i)∙ln (r_i+1/ r_i) называется полным термическим со-

               ^{i =1}

противлением многослойной цилиндрической стенки.    

   Тепловой поток через многослойную цилиндрическую стенку длиной l определится по формуле:

                                                                _{i =n}

                                 Q = π l (Т_с1 – Т_с2) / ∑(1/2λ_i)∙ln (r_i+1/ r_i).         (2.50)                                      

                                                                ^{i =1}

Для построения температурного поля многослойной стенки необходимо оценить температуру на поверхности каждого слоя в отдельности. Система уравнений (2.47) позволяет получить расчетные формулы для определения температуры на поверхности любого слоя:

 

                                Т_сл1 = Т_с1 - q _l (1/2πλ₁)ln (r₂/r₁),

 

                                 Т_сл2 = Т_сл1 - q _l (1/2πλ₂)ln (r₃/r₂),                   (2.51)

                                     

                                  Т_с2  = Т_сл2 – q _l (1/2πλ₃)ln (r₄/r₃).

    

Температурное поле многослойной цилиндрической стенки показано на рис. 2.7.

   При выводе формул для температурного поля и теплового потока теплопроводностью через многослойную цилиндрическую стенку мы предполагали, что все слои плотно прилегают один к другому и благодаря хорошему контакту соприкасающиеся поверхности разных слоев имеют одну и ту же температуру. В действительности на границе раздела двух слоев, так же как и в случае с многослойной плоской стенкой, зачастую имеет место неплотное соприкосновение поверхностей. Это приводит к возникновению контактного терми-ческого сопротивления. В результате уменьшается тепловой поток теплопроводностью через многослойную цилиндрическую стенку.

Повышение сопротивления тепловому потоку в месте контакта двух поверхностей обусловлено, как и в случае с многослойной плоской стенкой, меньшим коэффициентом теплопроводности газовой прослойки по сравнению с твердым телом, отклонением направления теплового потока от нормали к поверхности контакта, повышенным термическим сопротивлением поверхностного слоя из-за окисной пленки и загрязения. Надежные сведения о величинах контактного термического сопротивления получаются опытным путем.

   Контактное термическое сопротивление существенно уменьшается при покрытии соприкасающихся поверхностей мягкими металлами (медь, олово и др.) или при прокладках из мягких материалов.

 

                              Контрольные вопросы

 

1. Дифференциальное уравнение стационарной теплопроводности однослойной плоской стенки.
2. Уравнение стационарного температурного поля однослойной плоской стенки.
3. Уравнение плотности теплового потока через однослойную плоскую стенку при стационарной теплопроводности.
4. Термическое сопротивление однослойной плоской стенки при стационарной теплопроводности.
5. Опишите стационарное температурное поле многослойной плоской стенки.
6. Уравнение плотности теплового потока через многослойную плоскую стенку при стационарной теплопроводности.
7. Полное термическое сопротивление многослойной плоской стенки при стационарной теплопроводности.
8. Как влияет контактное термическое сопротивление на тепловой поток теплопроводностью через многослойную плоскую стенку.
9. Дифференциальное уравнение стационарной теплопроводности однослойной цилиндрической стенки.
10. Уравнение стационарного температурного поля однослойной цилиндрической стенки.
11. Уравнение плотности теплового потока через однослойную цилиндрическую стенку при стационарной теплопроводности.
12. Термическое сопротивление однослойной цилиндрической стенки при стационарной теплопроводности.
13. Опишите стационарное температурное поле многослойной цилиндрической стенки.
14. Уравнение теплового потока через многослойную цилиндри-ческую стенку при стационарной теплопроводности.
15. Полное термическое сопротивление многослойной цилиндри-ческой стенки при стационарной теплопроводности.
16. Как влияет контактное термическое сопротивление на тепловой поток через многослойную цилиндрическую стенку.

2.3. НЕСТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ

 

                    2.3.1 ОСНОВНЫЕ ПОЛОЖЕНИЯ

Если температурное поле меняется во времени, то тепловые процессы, протекающие в таких условиях, называют нестационарными.

Нестационарные процессы теплопроводности так же широко распространены в технике, как и стационарные. Это процессы нагревания или охлаждения тел.В режиме нестационарной теплопро-водности работают, например, регенеративные воздухоподогреватели котельных установок, в которых одна и та же поверхность нагрева омывается то горячим, то холодным теплоносителем (дымовыми газами или воздухом). При протекании горячих дымовых газов тепло воспри-нимается стенками воздухоподогревателя и в них аккумулируется. При протекании холодного воздуха это аккумулированное тепло им воспри-нимается.           

Другой пример – пропарочные камеры на заводах сборного железобетона, в которых для ускорения твердения бетона применяют его термовлажностную обработку, которая включает в себя периоды нагревания, изотермической выдержки (при максимальной температуре) и охлаждения.

  Передачу теплоты при нестационарном режиме можно определить, если найти закон изменения температурного поля и теплового потока во времени и в пространстве:

                      Т = f (x,y,z,t)   и       Q = φ (x,y,z,t).           (2.52)

 

При оценке нестационарного режима теплообмена цель расчета состоит в определении температурного состояния тела и количества полученной или отданной телом теплоты по истечении определенного периода времени.

Зависимость температуры не только от координат, но и от времени затрудняет графическое изображение даже одномерного температур-ного поля. На рис. 2.8,α показаны кривые изменения температуры тела в процессе его нагревания. При погружении тела в среду теплоносителя с постоянной температурой Т_ж сначала прогревается поверхность тела Т_ст, а спустя какое-то время начинает изменяться температура центра Т_ц. С увеличением времени прогрева температуры в теле выравниваются и при t → ∞ становятся равными температуре греющей жидкости. Характер изменения теплового потока, поступающего в тело при его нагревании, показан на рис. 2.8,b. Тело перед нагревом имело однород-ное температурное поле.

 

 

         Рис.2.8. Зависимость температуры стенки и количества         

              передаваемого тепла от времени при нагревании

 

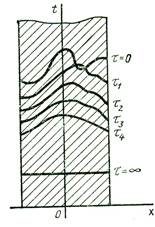
По мере прогрева тела количество воспринимаемой теплоты сначала резко увеличивается, достигает некоторого максимума, соответ-ствующего максимальной разности температур поверхности и центра, затем уменьшается и в пределе становится равной нулю. Площадь, ограниченная осью абсцисс и кривой Q= f (t), соответствует полному количеству теплоты, поступившему в тело за время t. Эта теплота аккумулируется телом и идет на повышение его энтальпии (теплосодержания).

Аналогичным образом протекает и процесс охлаждения тела, при этом его энтальпия уменьшается, а выделенная теплота передается в окружающую среду. На рис. 2.9 показано температурное поле для всех точек (точнее, изотермических поверхностей) однородной плоской стенки при одинаковых условиях охлаждения обеих ее поверхностей. При таком изображении поля температурное состояние можно охарактеризовать только в определенные моменты времени t.

    

Рис.2.9. Температурное поле однородной плоской стенки при

       одинаковых условиях охлаждения обеих ее поверхностей

 

Решение задачи нестационарной теплопроводности сводится к определению зависимости температуры и переданного количества теплоты от времени для любой точки тела. Однако такие решения могут быть получены при целом ряде упрощений и только для твердых тел простой формы – пластины, цилиндра и шара. Для практического использования эти решения обычно представляют в виде графиков.

Указанные зависимости могут быть найдены из решения дифференциального уравнения теплопроводности в твердом теле (без внутренних источников теплоты):

 

                                           ∂Т/ ∂t = α Ѳ Т.                                 (2.53)

 

Решение уравнения (2.53) содержит постоянные интегрирования, для определения которых воспользуемся граничными условиями третьего рода, т.е. зададимся характером взаимодействия тела с окружающей средой

                                       α (Т_ст– Т_ж) = - λ_ст(∂Т/ ∂n)_п=0,                 (2.54)

 

где   α – коэффициент теплоотдачи между жидкой (газообразной)    

                средой и поверхностью твердого тела;

        Т_ст – температура поверхности стенки;

        Т_ж  - температура окружающей среды;

        λ_ст - коэффициент теплопроводности стенки;

(∂Т/ ∂n)_п=0 - градиент температуры на поверхности стенки.

Физические параметры тела λ, с и ρ считаются постоянными, а начальное распределение температуры равномерным.

При одинаковой температуре во всех точках твердого тела, равной Т_о, в начальный момент процесса теплообмена временные (начальные) условия имеют простой вид:

                                        при  t = 0 Т = Т_о.                                                     (2.55)

 

Решение уравнения (2.53) с учетом граничных (2.54) и временных (2.55) условий дает уравнение температурного поля вида:

 

                      Т = f (α, λ, α, t, x, y, z, Т_о, Т_ср, l_о, l₁,..., l _n).           (2.56)

 

Из уравнения (2.56) видно, что температура зависит от большого числа переменных и постоянных параметров и решение его пред-ставляет весьма сложную математическую задачу. Подробное изложение решений имеется в специальных курсах по теплопередаче.

Анализ уравнения (2.56) показал, что температуру твердого тела целесообразно представить в виде безразмерной избыточной температуры, а переменные и постоянные параметры сгруппировать в три безразмерных комплекса.

Обозначим избыточную температуру в любой точке тела в произвольный момент времени через θ:

                                            

                                            θ = Т – Т_ж.                                         (2.57) 

.                                      

Для точек, расположенных на поверхности и в центре стенки (на оси цилиндра):

                           θ_ст = Т_ст – Т_ж;   θ_ц = Т_ц – Т_ж.                         (2.58)

 

Для начального момента времени:

                         

                                         θ_о = Т_о – Т_ж.                                          (2.59)

 

Тогда безразмерная избыточная температура:

 

                            θ/θ_о = (Т – Т_ж) / (Т_о – Т_ж).                                 (2.60)

 

Безразмерные комплексы:

  Bi = α l /λ – число Био;                                                             (2.61)

Fо = α t/ l ² – число Фурье;                                                          (2.62)

               ξ/ l    - безразмерная координата;

             ξ - координата (ξ = x – для стенки;  ξ = r -для цилиндра);

             l   - характерный линейный размер тела (l = δ – для

                 стенки, толщина которой равна 2δ; l = R – для цилиндра).

Числа Био и Фурье являются критериями теплового подобия (подроб-нее о теории подобия см. в разделе «Конвективный теплообмен»). Число Био представляет собой один из самых важных параметров теории теплопроводности. Им определяется характер соответствия между тем-пературными условиями в окружающей среде и распределением температуры в теле:

                                               

                                           Bi = α/(λ/ l).                                    

 

Число Bi является количественной мерой интенсивности теплообмена между поверхностью тела и окружающей средой, оцениваемой по сравнению с проводимостью λ/ l стенки.

Число Фурье является мерой скорости изменения температуры тела при неустановившемся тепловом состоянии:

    

                                          Fо = α t/ l ² = (λ/ l) l ²t / сρ l ³.                          

 

Fo представляет собой отношение масштаба количества теплоты (λ/ l) l ²t, притекающей вследствие теплопроводности, к масштабу изменения теплосодержания тела сρ l ³.

В результате решение дифференциального уравнения теплопровод-ности, описывающее нестационарное температурное поле в теле, имеет следующий вид:

                                                  _n=∞

                               θ/θ_о = ∑ A(μ_n)U(μ_n ξ/ l)exp(-μ_n²Fo),            (2.63)

                                          ⁿ⁼¹

где А и U - некоторые функции;

       μ_n – корни характеристического уравнения μ=μ(Bi).

Или в общем виде

                                          θ/θ_о = f (Fo, Bi, ξ/ l),                               (2.64)

 

вид функции в котором зависит от формы тела.

  

      2.3.2. ОХЛАЖДЕНИЕ (НАГРЕВ) ОДНОМЕРНЫХ ТЕЛ

Для одномерных тел (неограниченной пластины и бесконечно длинного цилиндра) дифференциальное уравнение теплопроводности (2.53) с учетом (2.57) приводится к виду:

для пластины

                                        ∂θ / ∂t =  α ∂²θ / ∂x²;                             (2.65)

для цилиндра

                            ∂θ / ∂t = α (∂²Т / ∂r² + (1/r)(∂Т / ∂r).             (2.66)                                 

       

При Fo ≥ 0,3 уравнение (2.62), описывающее изменение во времени безразмерной температуры θ_ц/θ_о на средней плоскости пластины (стенки) x = 0, оси цилиндра r = 0, примет вид:

 

                              θ_ц/θ_о = N(Bi)exp(-μ₁²Fo),                               (2.67)

 

а  на поверхностях этих тел:

 

                                 θ_ст/θ_о = P(Bi)exp(-μ₁²Fo),                             (2.68)

 

где N(Bi) и P(Bi) – функции, зависящие от Bi;

                   μ₁  - первый корень характер