
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение систем линейных алгебраических уравнений матричным методом (с помощью обратной матрицы).
Пусть система линейных алгебраических уравнений задана в матричной форме Так как Пример. Решите систему линейных уравнений Решение. Перепишем систему уравнений в матричной форме: Так как Построим обратную матрицу Осталось вычислить Ответ:
Основная проблема при нахождении решения систем линейных алгебраических уравнений матричным методом заключается в трудоемкости нахождения обратной матрицы, особенно для квадратных матриц порядка выше третьего. Более подробное описание теории и дополнительные примеры смотрите в статье матричный метод решения систем линейных уравнений. Билет 16 Билет 17 Множество решений системы линейных однородных уравнений с n переменными есть линейное подпространство арифметического пространства Аn. Размерность пространства решений системы линейных однородных уравнений равна n – r, где n – число неизвестных, r – ранг матрицы системы Базис пространства решений системы линейных однородных уравнений называется её фундаментальной системой решений. Если а – частное решение линейной неоднородной системы уравнений и а1, а2, …, аn–r – фундаментальная система решений соответствующей однородной системы уравнений, то общее решение данной неоднородной системы имеет вид d = а + С1а1 + С2а2 + … + Сn–r аn–r, где С1, С2, …, Сn–r – любые элементы поля Р. (Иными словами, общее решение системы линейных неоднородных уравнений равно сумме частного решения этой системы и общего решения соответствующей однородной системы.)
10. Матрица перехода от одного базиса лп к другому и ее свойства. Преобразование координат вектора при переходе к другому базису. Пусть в линейном пространстве Разложим векторы базиса e' по базису e: Матрицу Т = Свойства: Преобразование координат: Пусть в линейном пространстве a=e*[a]e=(e1,e2,…en) Тогда с одной стороны, а=е*[a]e, а с другой стороны а= e’[a]e’=(еТ)[a]e’ Из этих равенств получаем: а=e[a]e=е(Т[a]e'). Отсюда в силу единственности разложения вектора по базису е вытекает равенство [a]e = Т[a]e' (3), или
Билет 18
|
|||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 127; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.66.13 (0.007 с.) |
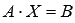 , где матрица A имеет размерность n на n и ее определитель отличен от нуля.
, где матрица A имеет размерность n на n и ее определитель отличен от нуля.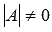 , то матрица А – обратима, то есть, существует обратная матрица
, то матрица А – обратима, то есть, существует обратная матрица 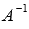 . Если умножить обе части равенства
. Если умножить обе части равенства  . Так мы получили решение системы линейных алгебраических уравнений матричным методом.
. Так мы получили решение системы линейных алгебраических уравнений матричным методом.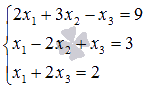 матричным методом.
матричным методом.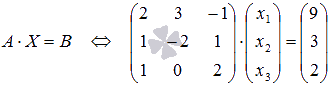
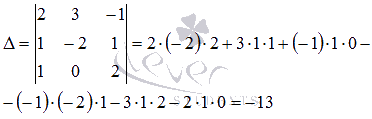 то СЛАУ можно решать матричным методом. С помощью обратной матрицы решение этой системы может быть найдено как
то СЛАУ можно решать матричным методом. С помощью обратной матрицы решение этой системы может быть найдено как 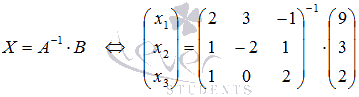 .
.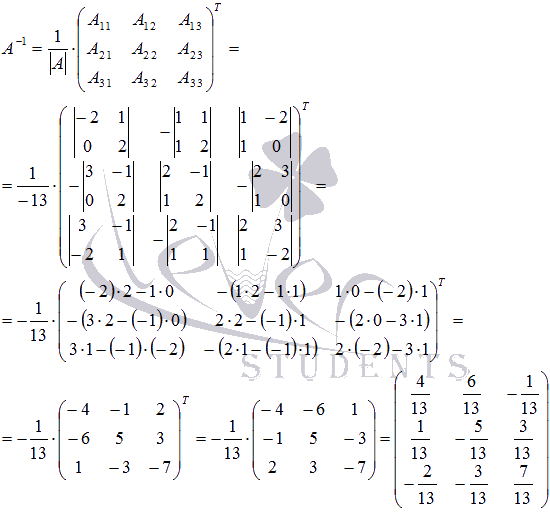
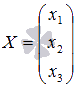 - матрицу неизвестных переменных, умножив обратную матрицу
- матрицу неизвестных переменных, умножив обратную матрицу 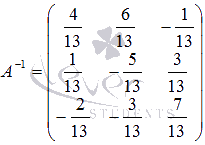 на матрицу-столбец свободных членов
на матрицу-столбец свободных членов 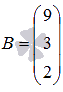 (при необходимости смотрите статьюоперации над матрицами):
(при необходимости смотрите статьюоперации над матрицами): 
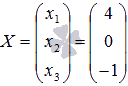 или в другой записи x1 = 4, x2 = 0, x3 = -1.
или в другой записи x1 = 4, x2 = 0, x3 = -1.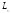 заданы два базиса: e = (e1, e2, …, en) (назовём его старым базисом) и
заданы два базиса: e = (e1, e2, …, en) (назовём его старым базисом) и 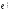 = (e1', e2', …, en') (назовём его новым базисом).
= (e1', e2', …, en') (назовём его новым базисом).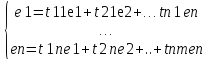
 называют матрицей перехода от базиса e кбазису
называют матрицей перехода от базиса e кбазису 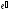 . Равенства в матричном виде удобно записывать так:
. Равенства в матричном виде удобно записывать так: 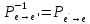 ,Матрица перехода невырожденная(квадратная, определитель не 0).
,Матрица перехода невырожденная(квадратная, определитель не 0).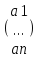 , [a]e’=
, [a]e’= 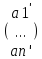 ,
,


