
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способ №1. Вычисление рангов по определению.
Согласно определению, ранг – это наивысший порядок миноров матрицы, среди которых есть хоть один, отличный от нуля. Обычно исследование начинают с миноров первого порядка, но здесь удобнее приступить сразу к вычислению минора третьего порядка матрицы A. Элементы минора третьего порядка находятся на пересечении трёх строк и трёх столбцов рассматриваемой матрицы. Так как матрица A содержит всего 3 строки и 3 столбца, то минор третьего порядка матрицы A – это определитель матрицы A, т.е. ΔA. Для вычисления определителя применим формулу №2 из темы "Формулы для вычисления определителей второго и третьего порядков": ΔA=∣∣∣∣−3−1492−2−7−419∣∣∣∣=−21. Итак, есть минор третьего порядка матрицы A, который не равен нулю. Минор четвёртого порядка составить невозможно, так как для него требуется 4 строки и 4 столбца, а в матрице A всего 3 строки и 3 столбца. Итак, наивысший порядок миноров матрицы A, среди которых есть хотя бы один не равный нулю, равен 3. Следовательно, rangA=3. Нам требуется найти также и rangA˜. Давайте посмотрим на структуру матрицы A˜. До черты в матрице A˜находятся элементы матрицы A, причём мы выяснили, что ΔA≠0. Следовательно, у матрицы A˜ есть минор третьего порядка, который не равен нулю. Миноров четвёртого порядка матрицы A˜ составить мы не можем, поэтому делаем вывод: rangA˜=3. Так как rangA=rangA˜, то согласно теореме Кронекера-Капелли система совместна, т.е. имеет решение (хотя бы одно). Чтобы указать количество решений, учтём, что наша СЛАУ содержит 3 неизвестных: x1, x2 и x3. Так как количество неизвестных n=3, то делаем вывод: rangA=rangA˜=n, поэтому согласно пункту №3следствия из теоремы Кронекера-Капелли, система является определённой, т.е. имеет единственное решение. Задача решена. Какие недостатки и преимущества имеет данный способ? Для начала поговорим о плюсах. Во-первых, нам понадобилось найти всего один определитель. После этого мы сразу сделали вывод о количестве решений. Обычно в стандартных типовых расчётах даются системы уравнений, которые содержат три неизвестных и имеют единственное решение. Для таких систем данный метод очень даже удобен, ибо мы заранее знаем, что решение есть (иначе примера не было бы в типовом расчёте). Т.е. нам остаётся только показать наличие решения наиболее быстрым способом. Во-вторых, вычисленное значение определителя матрицы системы (т.е. ΔA) пригодится после: когда станем решать заданную систему методом Крамера или с помощью обратной матрицы.
Однако метод вычисления ранга по определению нежелательно применять, если матрица системы Aявляется прямоугольной. В этом случае лучше применить второй метод, о котором пойдёт речь ниже. Кроме того, если ΔA=0, то мы ничего не сможем сказать о количестве решений заданной неоднородной СЛАУ. Может, СЛАУ имеет бесконечное количество решений, а может – ни одного. Если ΔA=0, то требуется дополнительное исследование, которое зачастую является громоздким. Подводя итог сказанному, отмечу, что первый способ хорош для тех СЛАУ, у которых матрица системы квадратна. При этом сама СЛАУ содержит три или четыре неизвестных и взята из стандартных типовых расчетов или контрольных работ. Способ №2. Вычисление ранга методом элементарных преобразований. Подробно это метод описан в соответствующей теме. Мы станем вычислять ранг матрицы A˜. Почему именно матрицы A˜, а не A? Дело в том, что матрица A является частью матрицы A˜, поэтому вычисляя ранг матрицы A˜ мы одновременно найдем и ранг матрицы A. A˜=⎛⎝⎜⎜−3−1492−2−7−419179−42⎞⎠⎟⎟→|меняем местами первую и вторую строки|→→⎛⎝⎜⎜−1−3429−2−4−719917−42⎞⎠⎟⎟r2−3r1r3+4r1→⎛⎝⎜⎜−100236−4539−10−6⎞⎠⎟⎟r3−2r2→→⎛⎝⎜⎜−100230−45−79−1014⎞⎠⎟⎟ Мы привели матрицу A˜ к ступенчатому виду. Полученная ступенчатая матрица имеет три ненулевых строки, поэтому её ранг равен 3. Следовательно, и ранг матрицы A˜ равен 3, т.е. rangA˜=3. Делая преобразования с элементами матрицы A˜ мы одновременно преобразовывали и элементы матрицы A, расположенные до черты. Матрица A также приведена к ступенчатому виду: ⎛⎝⎜−100230−45−7⎞⎠⎟. Вывод: ранг матрицы A также равен 3, т.е. rangA=3. Так как rangA=rangA˜, то согласно теореме Кронекера-Капелли система совместна, т.е. имеет решение. Чтобы указать количество решений, учтём, что наша СЛАУ содержит 3 неизвестных: x1, x2 и x3. Так как количество неизвестных n=3, то делаем вывод: rangA=rangA˜=n, поэтому согласно пункту №3 следствия из теоремы Кронекера-Капелли, система определена, т.е. имеет единственное решение.
Какие преимущества второго способа? Главное преимущество – это его универсальность. Нам совершенно неважно, является ли матрица системы квадратной или нет. Кроме того, мы фактически провели преобразования прямого хода метода Гаусса. Осталось лишь пару действий, и мы смогли бы получить решение данной СЛАУ. Честно говоря, второй способ нравится мне более первого, но выбор – это дело вкуса. Ответ: Заданная СЛАУ совместна и определена. Пример №2 Исследовать СЛАУ ⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪x1−x2+2x3=−1;−x1+2x2−3x3=3;2x1−x2+3x3=2;3x1−2x2+5x3=1;2x1−3x2+5x3=−4. на совместность. Решение Находить ранги матрицы системы и расширенной матрицы системы будем методом элементарных преобразований. Расширенная матрица системы: A˜=⎛⎝⎜⎜⎜⎜⎜⎜1−1232−12−1−2−32−3355−1321−4⎞⎠⎟⎟⎟⎟⎟⎟. Найдём требуемые ранги, преобразовывая расширенную матрицу системы: ⎛⎝⎜⎜⎜⎜⎜⎜1−1232−12−3−2−12−3553−13−412⎞⎠⎟⎟⎟⎟⎟⎟r2+r1r3−2r1r4−3r1r5−2r1→⎛⎝⎜⎜⎜⎜⎜⎜10000−11−1112−11−1−1−12−244⎞⎠⎟⎟⎟⎟⎟⎟r3−r2r4−r2r5+r2→ →⎛⎝⎜⎜⎜⎜⎜⎜10000−110002−1000−12220⎞⎠⎟⎟⎟⎟⎟⎟r4−r3→⎛⎝⎜⎜⎜⎜⎜⎜10000−110002−1000−12200⎞⎠⎟⎟⎟⎟⎟⎟ Расширенная матрица системы приведена к ступенчатому виду. Ранг ступенчатой матрицы равен количеству её ненулевых строк, поэтому rangA˜=3. Матрица A (до черты) тоже приведена к ступенчатому виду, и ранг её равен 2, rangA=2. Так как rangA≠rangA˜, то согласно теореме Кронекера-Капелли система несовместна (т.е. не имеет решений). Ответ: система несовместна. Пример №3 Исследовать СЛАУ ⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪2x1+7x3−5x4+11x5=42;x1−2x2+3x3+2x5=17;−3x1+9x2−11x3−7x5=−64;−5x1+17x2−16x3−5x4−4x5=−90;7x1−17x2+23x3+15x5=132. на совместность. Решение Приводим расширенную матрицу системы к ступенчатому виду: ⎛⎝⎜⎜⎜⎜⎜⎜21−3−570−2917−1773−11−1623−500−50112−7−4154217−64−90132⎞⎠⎟⎟⎟⎟⎟⎟→r1↔r3 →⎛⎝⎜⎜⎜⎜⎜⎜12−3−57−20917−1737−11−16230−50−50211−7−4151742−64−90132⎞⎠⎟⎟⎟⎟⎟⎟r2−2r1r3+3r1r4+5r1r5−7r1→⎛⎝⎜⎜⎜⎜⎜⎜10000−2437−331−2−120−50−5027−161178−13−513⎞⎠⎟⎟⎟⎟⎟⎟4r3+3r24r4−7r24r5+3r2→ →⎛⎝⎜⎜⎜⎜⎜⎜10000−2400031−11−11110−51515−1527−25−2525178−76−7676⎞⎠⎟⎟⎟⎟⎟⎟r4−r3r5+r2→⎛⎝⎜⎜⎜⎜⎜⎜10000−2400031−11000−5150027−2500178−7600⎞⎠⎟⎟⎟⎟⎟⎟ Мы привели расширенную матрицу системы и саму матрицу системы к ступенчатому виду. Ранг расширенной матрицы системы равен трём, ранг матрицы системы также равен трём. Так как система содержит n=5 неизвестных, т.е. rangA˜=rangA<n, то согласно пункту №2 следствия из теоремы Кронекера-Капелли данная система является неопределённой, т.е. имеет бесконечное количество решений.
Ответ: система является неопределённой. Во второй части мы разберём примеры, которые нередко включают в типовые расчёты или контрольные работы по высшей математике: исследование на совместность и решение СЛАУ в зависимости от значений параметров, входящих в неё. Билет 14 Пустьдана система n линейных уравнений с n неизвестными. или в матричной форме А*Х=В.Основная матрица А такой системы квадратная. Определитель этой матрицы
называется определителем системы. Если определитель системы отличен от нуля, то система называется невырожденной. Найдем решение данной системы уравнений в случае D¹0 Умножив обе части уравнения А*Х=В слева на матрицу A-1, получим A-1*A*X=A-1*B Поскольку. A-1*A=E и Е*Х=Х, то X=A-1*B (4.1) Расширенной матрицей системы называется матрица A системы, дополненная столбцом свободных членов
Отыскание решения системы по формуле (4.1) называют матричным способом решения системы. Матричное равенство (4.1) запишем в виде то есть
Отсюда следует, что
Но
Формулы Итак,невырожденная система n линейных уравнений с n неизвестными имеет единственное решение, которое может быть найдено матричным способом, либо по формулам Крамера
Правило Крамера. Если в системе
Доказательство. По теореме 14.1 обратная матрица находится по формуле
где
Поэтому
откуда и следует утверждение теоремы.
Билет 15
|
|||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 115; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.168.172 (0.013 с.) |






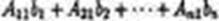 есть разложение определителя
есть разложение определителя по элементам первого столбца. Определитель D получается из определителяD путем замены первого столбца коэффициентов столбцом из свободных членов. Итак,
по элементам первого столбца. Определитель D получается из определителяD путем замены первого столбца коэффициентов столбцом из свободных членов. Итак,  Аналогично:
Аналогично:  , где D2получен из D путем замены второго столбца коэффициентов столбцом из свободных членов:
, где D2получен из D путем замены второго столбца коэффициентов столбцом из свободных членов:  ,...,
,..., 
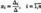 называются формулами Крамера.
называются формулами Крамера.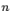 линейных уравнений с
линейных уравнений с  , то система имеет решение и притом единственное. Это решение задается формулами
, то система имеет решение и притом единственное. Это решение задается формулами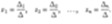

 -- алгебраические дополнения. Тогда из (15.3) следует, что
-- алгебраические дополнения. Тогда из (15.3) следует, что Заметим, что по формуле (14.13) разложение определителя
Заметим, что по формуле (14.13) разложение определителя  по первому столбцу в точности совпадает с первым элементом матрицы-столбца в правой части последнего равенства, разложение определителя
по первому столбцу в точности совпадает с первым элементом матрицы-столбца в правой части последнего равенства, разложение определителя  по второму столбцу дает второй элемент матрицы-столбца и т.д.
по второму столбцу дает второй элемент матрицы-столбца и т.д.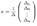 ,
,


