
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Блок задач на поиск расстояний.
Задача 126. Найти расстояние от точки Решение. По формуле
Задача 127. Найти расстояние от точки M1(1,4) до прямой Решение. Нормаль Задача 128. Найти расстояние между параллельными прямыми Решение. Заметим, что прямые действительно параллельны:
Для поиска расстояния применяется та же формула на одной прямой выбирается какая-либо точка, и ищется расстояние от этой точки до второй прямой. Для нахождения какой-либо точки можно присвоить одну переменную (проще всего присвоить 0) и вычислить вторую. Например, Ответ.
Задача 129. Найти 2 точки на оси Ох, отстоящие от прямой Решение. Применим формулу Мы ищем точки вида (с,0), ведь сказано, что они должны быть на оси Ох. Поэтому
Ответ. (-3,0) и (5,0).
Задача 130. Даны точки Вывести уравнение прямой, содержащей АВ, и найти расстояние от точки С до этой прямой (то есть высоту треугольника). Решение. Вектор АВ равен Теперь по формуле
Ответ. Прямая
Плоскость в пространстве. Задача 131. Построить уравнение плоскости, проходящей через точку A(1,2,3) перпендикулярно вектору Решение. Для произвольной точки
Ответ. Уравнение плоскости Замечание. Второй способ. Если мы уже знаем из теории, что координаты нормали это и есть коэффициенты A,B,C в уравнении плоскости, то можно сразу записать
Задача 132. Построить уравнение плоскости по точке (2,2,8) и перпендикуляру (3,3,7). Решение. Как и в прошлой задаче, берём произвольную точку Ответ.
Задача 133. Построить уравнение плоскости, проходящей через (0,0,0) параллельно 2 направляющим (1,1,2) и (2,1,3). Решение. Вектор от начала координат до произвольной точки Ответ.
Практика 14. Задача 134. Построить уравнение плоскости по точке Решение. Возьмём вектор
Из этого следует Ответ.
Задача 135. Построить уравнение плоскости по трём точкам. А(1,2,3), В(3,5,7), С(4,5,6). Решение. Здесь можно одну из точек, например А, рассматривать в качестве основной, а две другие помогут найти 2 направляющих вектора: АВ и АС. АВ = (2,3,4), АС = (3,3,3).
Для удобства вычислений, вынесли из определителя коэффициент 3. Можно сразу сократить на него правую и левую часть. Итак,
Сократим ещё на Ответ.
Задача 136. Найти расстояние от точки M1 (3,1,5) до плоскости Решение. По формуле
Ответ. Задача 137. Найти угол между двумя плоскостями: Решение. Нормали к этим плоскостям: Нормали не коллинеарны, то есть плоскости не параллельны, значит, они действительно пересекаются по какой-то прямой, и между ними есть какой-то угол.
Кстати, константа в уравнении одной из плоскостей никак не влияет на ответ, так как параллельный перенос плоскости не влияет на угол, который она образует с другой плоскостью. Ответ. Задача 138. Через точку
Решение. Если плоскость содержит ось и точку, то в ней по крайней мере содержится начало координат, и 2 такие направляющих: один проведён от (0,0,0) к точке А затем мы найдём угол между их нормалями. Эти плоскости можно представить так: две наклонные части крыши. Плоскость, перпендикулярная линии ОМ, не горизонтальна, так что угол между двумя частями такой крыши вовсе не 90 градусов. Чем более пологая крыша, тем ближе этот угол к 180, а чем более крутая, тем ближе к 90. Плоскость, перпендикулярная стыковочной линии крыши, а именно линии ОМ, показана жёлтым цветом.
Строим уравнение 1-й плоскости. Возьмём 3-й вектор, проведённый к какой-то произвольной точке
Нормаль к этой плоскости Строим уравнение 2-й плоскости. Аналогично, только (0,1,0).
Нормаль к этой плоскости Известно, что Тогда Замечание. Если бы надо было найти косинус наименьшего угла, то есть острого, то должны были бы рассматривать модуль
Вообще же, всегда имеется два угла, Прямая в пространстве
|
||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 80; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.86.155 (0.021 с.) |
 (1,4) до прямой
(1,4) до прямой  .
.  :
:  =
= 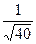 =
= 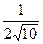 . Ответ.
. Ответ. 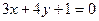 .
. . Тогда
. Тогда 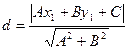 =
= 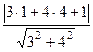 =
=  .
. и
и  .
.  , то есть пропорция сохраняется для всех коэффициентов, но нарушается для констант. Если бы уравнения были полностью пропорциональны, то это бы означало, что они задают одну и ту же прямую. А так они параллельны. Если бы не было пропорции и для коэффициентов, то прямые бы пересекались в одной точке.
, то есть пропорция сохраняется для всех коэффициентов, но нарушается для констант. Если бы уравнения были полностью пропорциональны, то это бы означало, что они задают одну и ту же прямую. А так они параллельны. Если бы не было пропорции и для коэффициентов, то прямые бы пересекались в одной точке. , тогда в первом уравнении
, тогда в первом уравнении  ,
,  , и точка
, и точка 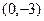 принадлежит первой прямой. Ищем расстояние от неё до 2-й прямой.
принадлежит первой прямой. Ищем расстояние от неё до 2-й прямой.  =
=  =
=  .
. .
. на расстояние
на расстояние 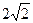 .
. 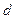 уже известно. В нашем примере должно быть
уже известно. В нашем примере должно быть 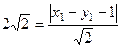 .
. ,
,  ,
,  . Две возможности:
. Две возможности: и
и  . На чертеже зелёным показаны кратчайшие пути от этих точек до прямой. Расстояния равны
. На чертеже зелёным показаны кратчайшие пути от этих точек до прямой. Расстояния равны 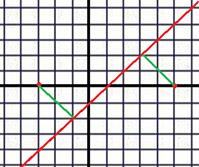
 ,
, 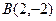 ,
,  .
. , и это есть направляющий на прямой. В то же время вектор АМ до произвольной точки
, и это есть направляющий на прямой. В то же время вектор АМ до произвольной точки 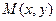 , который равен
, который равен  , пропорционален АВ. Тогда
, пропорционален АВ. Тогда  , то есть
, то есть  , и уравнение прямой:
, и уравнение прямой:  .
. .
.  =
=  =
= 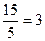 .
.
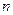 (1,4,2)
(1,4,2)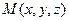 в плоскости, вектор
в плоскости, вектор  с координатами
с координатами  ортогонален
ортогонален  . Их скалярное произведение 0. Тогда
. Их скалярное произведение 0. Тогда 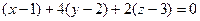 , т.е.
, т.е. .
. , а затем найти неизвестную D, используя условие, что точка (1,2,3) принадлежит плоскости:
, а затем найти неизвестную D, используя условие, что точка (1,2,3) принадлежит плоскости: 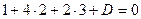 , откуда
, откуда 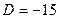 .
. ортогонален вектору
ортогонален вектору 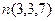 . Тогда
. Тогда  из чего следует
из чего следует  .
. , который сам имеет координаты
, который сам имеет координаты  =
=  .
. и двум направляющим векторам
и двум направляющим векторам 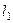 (4,2,3) и
(4,2,3) и  .
. в плоскости, тогда 3 вектора, а именно
в плоскости, тогда 3 вектора, а именно  ,
,  =
=  =
= 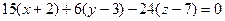 .
. . Такое уравнение можно сократить на 3, и получается
. Такое уравнение можно сократить на 3, и получается  .
.



 .
. 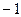 , получим
, получим 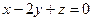 .
.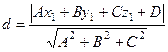 получаем, что
получаем, что =
=  =
=  =
=  .
. .
. и
и 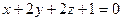 .
.  и
и  .
.  =
=  =
=  .
. , что приблизительно составляет 83,6 градусов.
, что приблизительно составляет 83,6 градусов.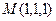 и ось Ох проходит одна плоскость, через эту же точку и ось Оу вторая. Найти тупой угол между этими плоскостями.
и ось Ох проходит одна плоскость, через эту же точку и ось Оу вторая. Найти тупой угол между этими плоскостями. , а второй - это просто базисный вектор оси, то есть для Ох вектор (1,0,0), а в случае оси Оу (0,1,0). Таким образом, уравнения каждой плоскости можно построить.
, а второй - это просто базисный вектор оси, то есть для Ох вектор (1,0,0), а в случае оси Оу (0,1,0). Таким образом, уравнения каждой плоскости можно построить.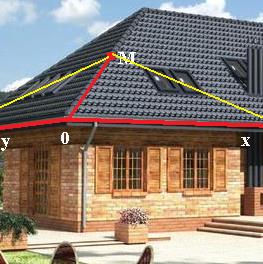
 ,
, 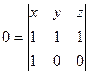 =
=  =
=  .
. .
. =
=  =
=  .
. .
. .
.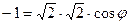 , т.е.
, т.е. 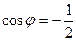 , угол 120 градусов.
, угол 120 градусов.  , чтобы угол получился именно в 1-й четверти, т.е. с положительным cos.
, чтобы угол получился именно в 1-й четверти, т.е. с положительным cos.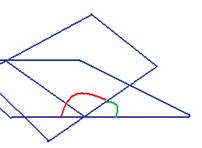
 и
и  . В зависимости от того, острый или тупой угол надо рассматривать, его косинус вычисляется как
. В зависимости от того, острый или тупой угол надо рассматривать, его косинус вычисляется как 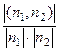 либо
либо 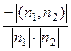 . Ответ.
. Ответ. 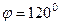 .
.


