
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Симплекс-метод решения задач линейного программирования
Стандартная форма задач линейного программирования Симплекс-метод (СМ) решения задач ЛП относится к числу итерационных методов, а это означает, что в процессе поиска оптимального решения выполняемые в определенной последовательности однотипные вычислительные процедуры повторяются до тех пор, пока это решение не будет получено. В основе построения СМ лежит положение о том, что опти- мальному решению всегда соответствует одна из угловых (или экстремальных) точек области допустимых решений. Исходя из этого в вычислительной процедуре СМ реализуется упоря- доченный процесс, при котором начиная с некоторой началь- ной допустимой угловой точки осуществляются переходы от одной допустимой угловой точки ОДР к другой. Каждый оче- редной переход осуществляется только в смежную (соседнюю) точку, при этом переход к предшествующей, уже пройденной экстремальной точке производиться не может. Перед каждым очередным переходом в смежную точку выполняется провер- ка на оптимальность той точки, которая в данный момент до- стигнута процедурой поиска оптимального решения СМ. Одна из главных трудностей, возникающих при организа- ции поиска СМ, заключается в определении начальной допус- тимой точки. С целью уменьшения этой трудности задачу ЛП приводят к стандартной форме, которая предполагает следу- ющее: 1. Все ограничения-неравенства представляются в виде равенств с неотрицательной правой частью. Для приведения ограничений, записанных в виде неравенств типа ≤ или ≥, к равенствам необходимо прибавить остаточную переменную к левой части ограничения типа ≤ или вычесть избыточную пе- ременную из левой части ограничения типа ≥. С содержатель- ной точки зрения остаточная переменная представляет собой остаток, неизрасходованную часть какого-то ресурса, а избы- точная переменная — превышение результатов деятельности над нормативными или плановыми заданиями. И на остаточ- ные, и на избыточные переменные также накладывается усло- вие неотрицательности. Правые части сформированных таким образом равенств всегда можно сделать неотрицательными, умножив обе части равенств на (-1). Пример 9.3. Даны ограничения-неравенства задачи ЛП: a11x1 + a12x2 ≤ b1, a21x1 + a22x2 ≥ b2, a31x1 + a32x2 ≤ -b3, x1, x2 ≥ 0.
Результатом приведения к стандартному виду является следующая система линейных равенств: a11x1 + a12x2 + s1 = b1, a21x1 + a22x2 − s2 = b2, -a31x1 − a32x2 − s3 = b3, x1, x2 ≥ 0, s1, s2, s3 ≥ 0. 2. На значения всех переменных задачи накладывается условие неотрицательности. Если какая-либо из переменных не имеет ограничения в знаке, то ее представляют в виде раз- ности двух неотрицательных переменных: xi = xi′ − xi″, где xi′, xi″ ≥ 0. Представленную таким образом переменную подставля- ют во все ограничения и в целевую функцию. Пример 9.4. Дана задача ЛП: найти max W(x) = c1x1 + c2x2 при ограничениях a11x1 + a12x2 ≤ b1, a21x1 + a22x2 ≥ b2, x1 ≥ 0, x2 — не ограничена в знаке. Выполнение условия неотрицательности всех переменных приводит к следующей задаче: найти max W(x) = c1x1 + c2x′2 − c2x″2 при ограничениях: a11x1 + a12x′2 − a12x″2 ≤ b1, a21x1 + a22x′2 − a22x″2 ≥ b2, x1 ≥ 0, x′2, x″2 ≥ 0. в) целевая функция задачи ЛП, представленной в стандарт- ной форме, может подлежать как максимизации, так и мини- мизации. Исходную ЦФ в ряде случаев можно изменить: мак- симизация некоторой ЦФ эквивалентна минимизации той же ЦФ, взятой с противоположным знаком, и наоборот. Например, задача максимизации ЦФ W(x) = x1 + 4x2 эквивалентна задаче минимизации ЦФ (-W(x)) = (-1)x1 + (-4)x2.
Основные понятия симплекс-метода Если задача ЛП имеет ограничения только типа ≤, трудно- стей в получении начального допустимого решения не возника- ет. В результате приведения задачи ЛП к стандартной форме ограничения задачи образуют систему линейных уравнений с n неизвестными, образующими векторное пространство, раз- мерность которого m определяется количеством ограничений исходной задачи. При m = n система уравнений имеет единс- твенное решение, при m > n в задаче ЛП возникает избыточ- ность (часть уравнений оказывается лишней), и при m < n зада- ча ЛП будет иметь бесчисленное множество решений. Именно этот последний случай и рассматривается в теории линейного программирования. Пример 9.5. Задача ЛП из примера 9.1 после приведения к стандартной форме приобретает вид: найти max W(x) = x1 + 4x2 + 0s1 + 0s2 при ограничениях:
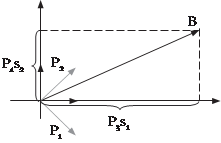
x1 + x2 + s1 = 4, - x1 + x2 + s2 = 2, x1, x2 ≥ 0, s1,s2 ≥ 0. Для этой задачи m = 2, а n = 4. Всякая угловая точка ОДР соответствует базисному ре- шению задачи ЛП, представленной в стандартной форме. Для определения понятия базисного решения рассмотрим систему линейных уравнений из примера 9.5. Коэффициенты при пе- ременных и правые части ограничений этой системы являют- ся координатами m-мерных векторов: P1 = (1; -1), P = (1; 1),
можно записать в векторной форме: P1x1 + P2x2 + P3s1 + P4s2 = B. Каждая остаточная переменная вводится только в одно ограничение, поэтому в остальных ограничениях коэффици- енты при этой переменной, естественно, будут равны нулю. По этой причине в рассматриваемой системе линейных уравнений векторы P3, P4 являются линейно независимыми единичными векторами, т. е. составляют базис всей приведенной системы векторов. Переменные s1, s2, в данном случае соответствующие векторам базиса, называются базисными, а переменные x1, x2 — небазисными, или свободными. С геометрической точки зрения роль базисных переменных состоит в том, что они опре- деляют величину проекции вектора B на направления векторов базиса (рис. 9.3). С введением остаточных переменных базисное решение получить нетрудно. Базисным решением является такое час- тное решение системы линейных уравнений, которое получено следующим образом: все (n − m) свободных переменных при- равниваются нулю, а m базисных переменных, в качестве ко- торых и выступают остаточные переменные, приравниваются правым частям уравнений.
Рис. 9.3. Векторное представление ограничений задачи ЛП
Если базисное решение удовлетворяет условию неотри- цательности правых частей, то оно называется допустимым базисным решением. Исходной точкой поиска в СМ является начало координат. Решение, удовлетворяющее этой точке, на- зывается начальным. Для задачи ЛП из примера 9.5 начальным допустимым базисным решением является следующее: в ка- честве базисных принимаются остаточные переменные, кото- рые принимают значения s1 = 4, s2 = 2, остальные переменные x1, x2 являются в этом случае свободными и приравниваются нулю. Таким образом, для задачи ЛП, имеющей ограничения только типа ≤, начальное допустимое базисное решение полу- чается после приведения ее к стандартному виду. С помощью метода исключений Жордана — Гаусса можно найти все базисные решения системы уравнений, последова- тельно переходя от одного единичного базиса к другому. Общее количество таких базисных решений определяется количест- вом сочетаний максимальное количество итераций, которое может быть вы- полнено при решении задачи ЛП симплекс-методом. Однако на самом деле количество таких итераций гораздо меньше, пос- кольку в симплекс-методе реализуется такой целенаправлен- ный процесс перехода от одной экстремальной точки к другой, что в результате происходит увеличение значения ЦФ (в зада- че ее максимизации). Смежные экстремальные точки ОДР различаются толь- ко одной переменной в каждой группе базисных и свободных переменных. Например, на рис. 9.1 началу координат соответс- твуют базисные переменные s1, s2 и небазисные x1, x2. Для со- седней точки F группу базисных переменных составляют x1 и s2, а группу небазисных — x2 и s1. Как видно, группы базисных и небазисных переменных в точках О и F действительно разли- чаются лишь одной компонентой. Это свойство экстремальных точек позволяет определить каждую последующую смежную экстремальную точку путем замены одной из текущих неба- зисных переменных текущей базисной переменной.
Для рассмотрения этого процесса взаимной замены пере- менных вводятся понятия включаемой и исключаемой пере- менных. Включаемая переменная — это небазисная в данный момент переменная, но которая будет включена в состав базис- ных на следующей итерации. Исключаемая переменная — это переменная, которая на следующей итерации будет исключена из состава базисных.
Алгоритм симплекс-метода Рассмотрим задачу ЛП примера 9.5. Процедуру решения задачи с использованием СМ удобнее представить с помощью табл. 9.2, которая является реализацией обычной жордановой таблицы. В левом столбце таблицы отображаются номер итерации и указываются включаемые и исключаемые на очередной ите- рации переменные. В столбце “Базис. перем” вписываются ба- зисные на данной итерации переменные. Столбец “Решения” содержит правые части ограничений задачи ЛП на нулевой итерации, базисные решения, получаемые в ходе очередной итерации, в этом же столбце будет находиться и оптимальное решение задачи. В столбце “Условия допустимости” содержит- ся отношение, с помощью которого осуществляется проверка условий допустимости при выборе переменной, исключаемой из состава базисных. Столбец “Контрольная сумма” служит для проверки правильности проводимых расчетов и в каждой клеточке содержит арифметическую сумму всех чисел соот- ветствующей строки. Остальные столбцы содержат в заголовке имена всех базисных и небазисных переменных. Шаг 0. Используя стандартную форму задачи ЛП опреде- лить начальное допустимое базисное решение (НДБР), прирав- няв нулю (n − m) свободных переменных. На этом шаге строится исходная таблица и в нее заносятся все базисные переменные, коэффициенты при переменных в ограничениях, а также их правые части. Для ЦФ в таблице вводится отдельная строка (W(x)-строка). Для включения в таблицу ЦФ преобразуют пу- тем переноса ее правой части влево от знака равенства, напри- мер, W(x) − x1 − 4x2 − 0s1 − 0s2 = 0. Таблица 9.2
Шаг 1. Из числа текущих небазисных переменных выби- рается включаемая в базис новая переменная, положительное приращение которой приводит к увеличению ЦФ. На этом шаге проверяется условие оптимальности: в задачах максимизации ЦФ, включаемой в состав базисных, является переменная, которая имеет наибольший отрицательный коэффициент в Z−строке симплекс-таблицы. Если все коэффициенты Z−строки оказались положительными, то это свидетельствует о достиже- нии ЦФ оптимального значения. В задачах минимизации ЦФ признаком оптимальности решения является отрицательность всех коэффициентов Z−строки. Переменная, включаемая в со- став базисных, определяет ведущий столбец таблицы. Шаг 2. Из числа переменных текущего базиса выбирается исключаемая переменная, которая должна принять нулевое значение. На этом шаге проверяется условие допустимости: в задачах и максимизации, и минимизации ЦФ исключаемой выбирается та базисная переменная, для которой отношение постоянной в правой части соответствующего ограничения к положительному коэффициенту ведущего столбца мини- мально, т. е. si = min{b1/a11; b2/a21}. Существо этой проверки состоит в том, что следующая экстремальная точка, в ко- торую будет осуществлен переход, должна принадлежать ОДР. Величина отношения определяет приращение, которое получает включаемая в состав базисных переменная. Пере- менная, исключаемая из состава базисных, определяет веду- щую строку. Шаг 3. Находится новое базисное решение, соответству- ющее новым базисным и небазисным переменным. Элемент таблицы на пересечении ведущей строки и ведущего столбца называется ведущим. Очередная итерация проводится по сле- дующей схеме: 1) все элементы ведущей строки делятся на ведущий эле- мент; 2) все элементы ведущего столбца заменяются нулями, а сам ведущий элемент — единицей; 3) все остальные элементы симплекс-таблицы, включая Z-строку и элементы столбцов “Решение” и “Контрольная сум- ма”, вычисляются по правилу “прямоугольника”
где a ks — ведущий элемент. Осуществляется переход к шагу 1.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 184; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.53.143 (0.021 с.) |
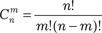 , которое по своей сути отражает
, которое по своей сути отражает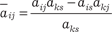 ,
,


