Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача на пропорциональное деление ⇐ ПредыдущаяСтр 3 из 3
М4М, ч.2, стр. 17
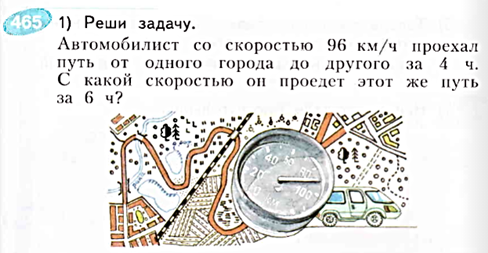
Задача на движение на нахождение 4-го пропорционального 1 вида М4М, ч.2, стр. 27
Задача на нахождение неизвестного по двум разностям 1 вида М4М, ч.2, стр. 60
Программа Истоминой: Нетиповая составная задача М4И, ч.2, стр. 42
Нетиповая составная задача М4И, ч.2, стр. 45
Задача на 4-пропорциональное М4И, ч.2, стр. 71
Задача на 4-пропорциональное М4И, ч.2, стр. 55
Задачи на нахождение неизвестного по двум разностям М4И, ч.2, стр. 61
Программа Аргинской: Задача на 4-пропорциональное М3А, ч. 2, стр. 105
Нетиповая составная задача М3А, ч. 2, стр. 100
Нетиповая составная задача М4А, ч. 2, стр. 72
4. Какую подготовительную работу необходимо провести прежде, чем познакомить учащихся с новым видом задач на движение – на движение в противоположных направлениях (на сближение и удаление друг от друга)? Приведите примеры таких заданий, подберите из учебников или придумайте самостоятельно, Какие методические приемы может использовать учитель при ознакомлении младших школьников с задачами на движение в противоположных направлениях? Какие новые понятия вводятся? Какие виды таких задач можно выделить? Среди составных задач особое внимание должно быть уделено задачам на встречное движение и в противоположных направлениях. Содержание этих задач включает новый элемент: здесь представлено совместное движение двух тел, что требует специального рассмотрения.
До введения задач на встречное движение важно провести соответствующую подготовительную работу. Надо познакомить с движением двух тел навстречу друг другу. Такое движение могут продемонстрировать в классе вызванные ученики. Например, два ученика начинают двигаться одновременно от двух противоположных стен навстречу друг другу, а при встрече останавливаются. Одноклассники наблюдают, что расстояние между пешеходами все время уменьшалось, что, встретившись, они прошли все расстояние от стены до стены, и что каждый из них затратил на движение до встречи одинаковое время. Под руководством учителя выполняется чертеж. Ещё можно провести наблюдение на улице за движением пешеходов, велосипедистов, автомобилей. Расширить представления учащихся о встречном движении можно попутно с решением задач из учебника. С помощью упражнений надо выяснить, что значит 'вышли одновременно' пешеходы, автомашины и т. п. и что при этом они были в пути до встречи одинаковое время. Необходимо также, чтобы дети твердо усвоили связь между величинами: скоростью, временем и расстоянием при равномерном движении, т. е. умели решать соответствующие простые задачи. Прежде чем ввести задачи на встречное движение очень важно сформировать правильные понятия об одновременном движении двух тел. Важно, чтобы дети уяснили, что если два тела вышли одновременно навстречу друг другу, то до встречи они будут в пути одинаковое время и пройдут все расстояние. Чтобы дети осознали это, следует включать задачи-вопросы, аналогичные следующим: 1. Из двух городов одновременно отплыли навстречу друг другу два теплохода и встретились через 3 часа. Сколько времени был в пути каждый теплоход? 2. Из деревни в город вышел пешеход и в это же время из города навстречу ему выехал велосипедист, который встретил пешехода через 40 минут. Сколько времени был в пути до встречи пешеход? Теперь можно ознакомить детей с решением задач на встречное движение. Целесообразно на одном уроке ввести все 3 вида, получая новые задачи путем преобразования данных в обратные. Такой прием позволяет детям самостоятельно найти решение, поскольку задача нового вида будет получена из задачи, уже решенной детьми.
На последующих уроках проводится работа по закреплению умения решать задачи рассмотренных видов. Здесь так же, как и при решении других задач, полезно предлагать различные упражнения творческого характера. В частности, ставится вопрос вида: «Могли ли велосипедисты (теплоходы, пешеходы и т.п.) встретиться на середине пути? При каких условиях? Если велосипедисты после встречи будут продолжать движение, то какой их них придет раньше к месту выхода другого велосипедиста, если будет двигаться с той же скоростью и др.? Также в 4 классе вводятся задачи на противоположное движение. Каждая из этих задач имеет 3 вида в зависимости от данных и искомого. I вид – даны скорость каждого из тел и время движения, искомое – расстояние; II вид – даны скорость каждого из тел и расстояние, искомое – время движения; III вид – даны расстояние, время движения и скорость одного из тел, искомое – скорость другого тела. Ознакомление с задачами на движение в противоположных направлениях может быть проведено аналогично введению задач на встречное движение. Проводя подготовительную работу, надо, чтобы дети пронаблюдали движение двух тел (пешеходов, машин, катеров и т.д.) при одновременном выходе их одного пункта. Они должны заметить, что при таком движении расстояние между движущимися телами увеличивается. При этом надо показать, как выполняется чертеж. При ознакомлении с решением задач этого вида тоже может на одном уроке решать три взаимообратные задачи, после чего выполнить сначала сравнение задач, а затем их решений. На этапе закрепления умения решать такие задачи ученики выполняют различные упражнения, как и в других случаях, в том числе проводят сравнение соответствующих задач на встречное движение и движение в противоположных направлениях, а также сравнение решений этих задач. Далее учащиеся будут решать составные задачи на нахождение четвертого пропорционального, на пропорциональное деление, на нахождение неизвестного по двум разностям с величинами s, t, v. Задачи на пропорциональное деление вводятся по-разному: можно предложить для решения готовую задачу, а можно сначала составить ее, преобразовать задачу на нахождение четвертого пропорционального, в задачу на пропорциональное деление, и после их решения сравнить как сами задачи, так и их решения. Обобщению умения решать задачи рассмотренного вида помогают упражнения творческого характера. До решения полезно спросить, на какой из вопросов задачи получается в ответе большее число и почему, а после решения проверить, соответствуют ли этому виду полученные числа, что является одним из способов проверки решения. Можно далее выяснить, могли ли получиться в ответе одинаковые числа и при каких условиях. При решении задач на движение в качестве средств наглядности, как правило, используются схематические чертежи, так как чертеж помогает правильно определять и представлять жизненную ситуацию, отраженную в задаче. Однако в некоторых задачах на чертеже не всегда удается показать все величины и связи между ними, а также обозначить вопрос. Приведем в качестве примера задачу: «Моторная лодка прошла путь от одной пристани до другой за 20 мин со скоростью 625 м/мин. На обратный путь она затратила на 5 мин больше. На сколько меньше была скорость лодки на обратном пути?»
Выяснив, что величины, фигурирующие в задаче – это время, скорость, расстояние, и опорные слова – туда и обратно, выполняется запись в следующем виде:
Далее выясняется, что для ответа на вопрос задачи необходимо найти скорость, с которой лодка двигалась обратно, а для этого нужно знать время и расстояние. Время, потраченное на обратный путь, находим сложением: 20 + 5 = 25 (мин). Теперь находим расстояние. Расстояние равно скорости, умноженной на время, а так как оно при движении туда и обратно одинаковое, то 625 х 20 = 12500(м), а скорость равна расстоянию, деленному на время: 12500: 25 =500 (м/мин). Теперь можно ответить на вопрос задачи. Для этого из большей скорости вычитаем меньшую: 625 – 500 = 125 (м/мин) Сделав такую запись, учащимся проще ориентироваться в выборе порядка выполнения действий и знака выполняемого действия, так как в ней необходимы знания не только о взаимосвязях между величинами «скорость», «время», «расстояние», но и умения решать простые задачи на увеличение числа на несколько единиц и задач на разностное сравнение. Таким образом, после ознакомления со скоростью движения и изучения связи между величинами, скорость, время, расстояние, необходимо сформировать у детей умения и навыки решения задач на встречное движение и движение в противоположных направлениях различных видов, а также умение решать и составлять задачи по чертежам и таблицам.
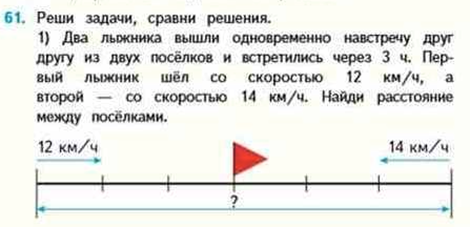
Задача на движение навстречу друг другу, на сближение М4М ч.2, стр.16, №61
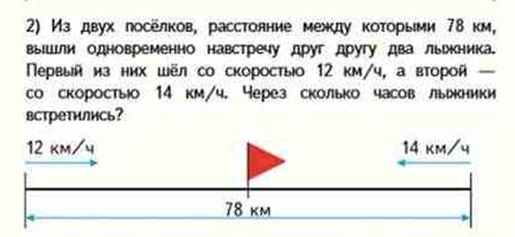
На нахождение времени движения. М4М ч.2, стр.16
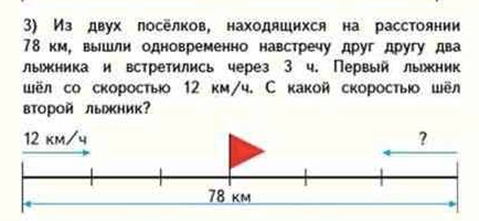
На нахождение скорости одного из движущихся М4М ч.2, стр.16
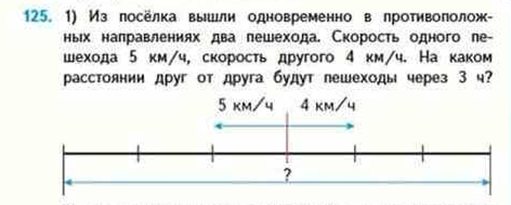
Задача на движение в противоположные стороны, удаление
М4М ч.2, стр. 33, №125
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 1081; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.56.45 (0.018 с.) |















 625 м/мин? на?<
625 м/мин? на?<