
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отчет по практическим работамСтр 1 из 6Следующая ⇒
Отчет по практическим работам Вариант 2 1
Решение: Введем дополнительные переменные y 1, y 2, y 3, y 4. Причем в третье неравенство введем неотрицательную переменную y 3 со знаком плюс, а в первое, второе и четвертое – со знаком минус переменные y 1, y 2, y 4 запишем задачу в виде:
Перейдем от задачи нахождения максимума целевой функции к задаче нахождения минимума, помножив целевую функцию на (-1)
Таким образом, мы перешли от произвольной ЗЛП к эквивалентной ей ОЗЛП. По правилу приведения ЗЛП к ОЗЛП, если в исходной задаче некоторое ограничение было неравенством, то оно преобразуется в равенство, введением в левую часть некоторой неотрицательной переменной.
Цель: Отработать и закрепить умения графически решать системы неравенств, с двумя переменными. Вариант 11.
Решение: Для построения математической модели остается только идентифицировать переменные и представить цель и ограничения в виде математических функций этих переменных.
Таким образом, мы приходим к следующей математической задаче: среди всех неотрицательных решений данной системы линейных неравенств требуется найти такое, при котором функция F принимает максимальное значение F max. Построим многоугольник решений. Для этого в системе координат X1 X2 на плоскости изобразим ограниченные прямые:
Взяв какую-либо точку, например, начало координат, установим, какую полуплоскость определяет соответствующее неравенство. Полуплоскости, определяемые неравенствами, на рисунке показаны стрелками. Области решений нет, функция не ограничена сверху.
Цель: Отработать и закрепить умения решения ЗЛП симплекс-методом. Вариант 9. Найти максимум функции
Если система ограничений имеет вид:
Решение:
Для составления симплекс-таблиц систему ограничений и функцию F необходимо представлять и в следующем виде:
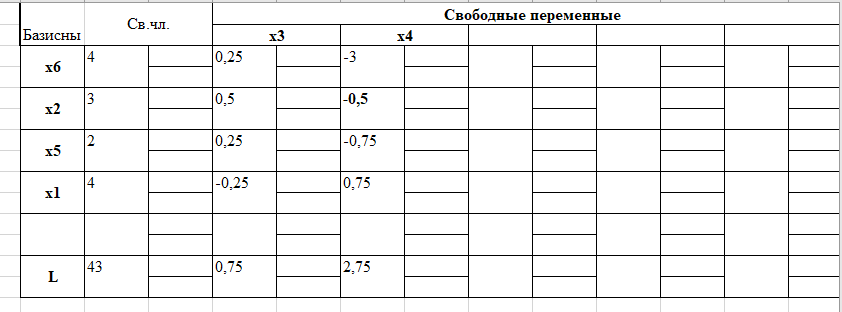
Первый шаг симплекс-метода, составляем таблицут1.1
Таблица 1.1
Ответ: Х = (4,3,0,0,2,4) L = 43 Цель: 1. Отработать и закрепить умения записывать условие транспортной задачи в виде математических формул. 2. Отработать и закрепить умения записывать взаимосвязь показателей транспортной задачи в виде математической модели.
Определение переменных Обозначим количество изделий, выпускаемых из i-го филиала в j-ый пункт потребления через Задание ЦФ
Задание ограничений:
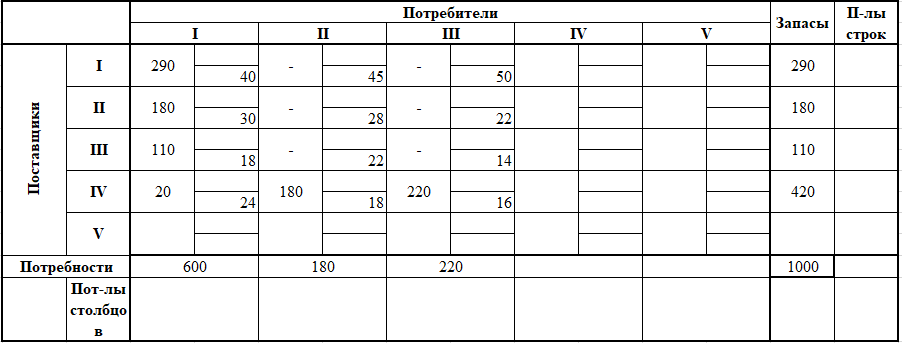
Цель: 1. Отработать и закрепить умения строить опорный план транспортной задачи двумя методами: методом северо-западного угла и методом наименьшей стоимости. 2. Отработать и закрепить умение находить оптимальное решение транспортной задачи методом потенциалов.
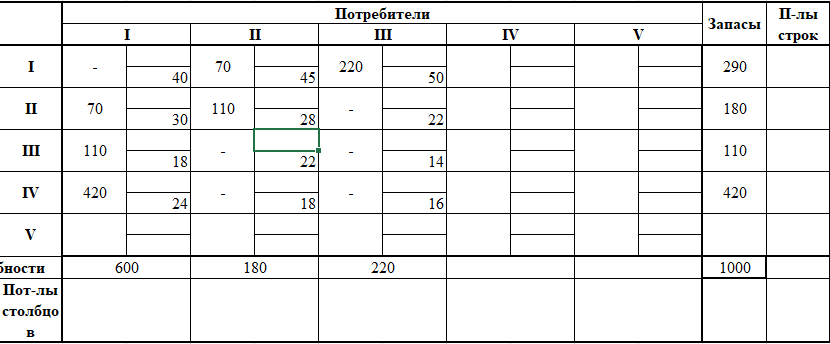
Решение: 1. Построим план двумя методами: методом северо-западного угла и методом наименьшей стоимости, и выберем тот план, который будет наилучшим, то есть получим минимальные затраты на перевозку однородного груза. А) Строим начальный план методом северо-западного угла. Составим таблицу значений:
начальный план
невыраженный. При таком плане суммарные транспортные издержки равны:
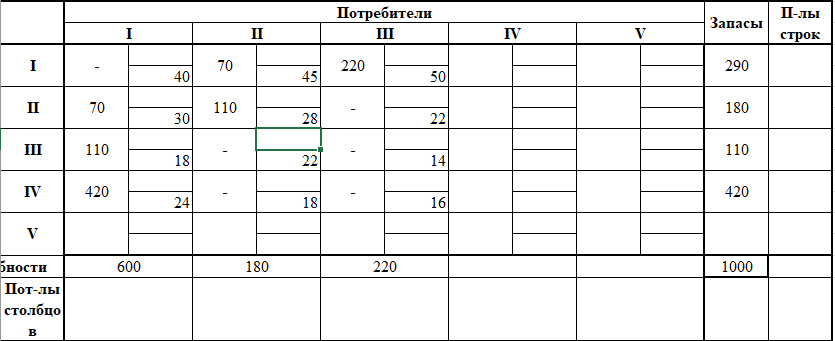
Б) Строим начальный план методом наименьшей стоимости. Составим таблицу значений:
Начальный план:
При таком плане транспортные издержки
Сравнивая транспортные издержки, видим, что план, построенный методом наименьшей стоимости, лучший. 2. Выбираем лучший план и находим потенциалы поставщиков и потребителей, используя первое условие оптимальности плана:
Производственное объединение состоит из 4 предприятий (n = 4). Общая сумма капитальных вложений равна 700 млн. руб. (b = 700), выделяемые предприятием суммы кратны 100 млн. руб. Если j-е предприятие получает инвестиции в объеме Е млн. руб. в год, то прирост годовой прибыли на этом предприятии составит
Требуется найти такое распределение инвестиций между предприятиями, которое максимизирует суммарный прирост прибыли на всех предприятиях вместе. Для этого необходимо составить математическую модель динамической задачи распределения инвестиций и решить ее методом динамического программирования, основывая каждый шаг вычислительного процесса.
Решение: Составим математическую модель динамической задачи распределения инвестиций и решим ее методом динамического программирования. В качестве шага управления примем вложение инвестиций в одно предприятие. Количество шагов равно количеству предприятий. Рассмотрим алгоритм с конца. Предположим на последнем шаге мы распределяем средства в четвертое предприятие. Зависимость прироста прибыли Рассмотрим предпоследний шаг задачи. На данном шаге нам необходимо рассмотреть суммарный прирост прибыли на двух предприятиях от совместного вложения инвестиций в них, пусть это будут предприятия 4 и 3. Необходимо найти условный оптимальный прирост прибыли на этих двух предприятиях, при условии вложения определенной суммы инвестиций в оба предприятия. Заполним таблицу, в верхнюю строку которой выпишем значения прироста прибыли четвертого предприятия от объема инвестиций - Значения (Табл. 1)
E - x3 | 0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
F3(x3)/F4(E - x4) | 0 | 61 | 80 | 93 | 100 | 106 | 112 | 116 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0 | 0 | 0 | 61 | 80 | 93 | 100 | 106 | 112 | 116 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
100 | 50 | 50 | 111 | 130 | 143 | 150 | 156 | 162 |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
200 | 68 | 68 | 129 | 148 | 161 | 168 | 174 |
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
300 | 82 | 82 | 143 | 162 | 175 | 182 |
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
400 | 92 | 92 | 153 | 172 | 185 |
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
500 | 100 | 100 | 161 | 180 |
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
600 | 107 | 107 | 168 |
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
700 | 112 | 112 |
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Составим таблицу 2:
· В верхнюю строку выпишем возможный объем инвестиций, выделяемый на 2 предприятия: Е.
· Во вторую строку запишем условно оптимальное значение суммарного прироста прибыли на двух предприятиях - 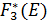 соответствующее объему инвестиций из строки 1.
соответствующее объему инвестиций из строки 1.
· Третью строку заполним значениями 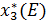 – объем инвестиций, приходящийся на второе предприятие.
– объем инвестиций, приходящийся на второе предприятие.
(Табл. 2)
| E | 0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
| F3*(E) | 0 | 61 | 111 | 130 | 148 | 162 | 175 | 185 |
| X3*(E) | 0 | 0 | 100 | 100 | 200 | 300 | 300 | 400 |
Рассмотрим предыдущий шаг, на котором изучим возможный прирост прибыли на трех предприятиях от совместного вложения объема инвестиций Е в них, пусть это будут предприятия 4,3 и 2, и найдем оптимальный вариант их распределения. Для этого в верхнюю строку выпишем значения условно оптимального прироста прибыли от объема инвестиций - 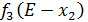 , вложенных в предприятии 4 и3 из таблицы 2. В левый столбец выпишем значения
, вложенных в предприятии 4 и3 из таблицы 2. В левый столбец выпишем значения 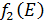 – прироста прибыли второго предприятия от объема инвестиций. Заполним ячейки таблицы значениями суммы этих величин.
– прироста прибыли второго предприятия от объема инвестиций. Заполним ячейки таблицы значениями суммы этих величин.
|
|
Как и на предыдущем шаге найдем максимальное значение суммарного прироста прибыли от различных вариантов распределения определенного объема инвестиций между предприятиями.
(Табл. 3)
| x2 |
E - x2 | 0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
|
F2(x2)/F3(E - x2) | 0 | 61 | 111 | 130 | 148 | 162 | 175 | 185 | |
| 0 | 0 | 0 | 61 | 111 | 130 | 148 | 162 | 175 | 185 |
|
100 | 30 | 30 | 91 | 141 | 160 | 178 | 192 | 205 |
|
|
200 | 52 | 52 | 113 | 163 | 182 | 200 | 214 |
|
|
|
300 | 76 | 76 | 137 | 187 | 206 | 224 |
|
|
|
|
400 | 90 | 90 | 151 | 201 | 220 |
|
|
|
|
|
500 | 104 | 104 | 165 | 215 |
|
|
|
|
|
|
600 | 116 | 116 | 177 |
|
|
|
|
|
|
|
700 | 125 | 125 |
|
|
|
|
|
|
|
По данным таблицы 3 составим таблицу 4, в которой:
· В верхнюю строку выпишем возможный объем инвестиций, выделяемый на три предприятия: Е.
· Во вторую строку запишем условно оптимальное значение суммарного прироста прибыли на двух предприятиях - 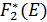 соответствующее объему инвестиций из строки 1.
соответствующее объему инвестиций из строки 1.
· Третью строку заполним значениями 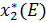 – объем инвестиций, приходящийся на второе предприятие.
– объем инвестиций, приходящийся на второе предприятие.
(Табл. 4)
| E | 0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
| F2*(Е) | 0 | 61 | 111 | 141 | 163 | 187 | 206 | 224 |
| X2*(E) | 0 | 0 | 0 | 100 | 200 | 300 | 300 | 300 |
Так как по условию задачи вложения инвестиций осуществляются в 4 предприятия, то переходим к последнему этап поиска условно оптимального вложения средств, рассмотрев вложения в четыре предприятия. Для этого составим таблицу аналогично 3. В верхнюю строку таблицы 5 выпишем значения условно оптимального прироста прибыли от объема инвестиций - 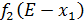 , вложенных в предприятия 4,3 и 2 из таблицы 4. В левый столбец выпишем значения
, вложенных в предприятия 4,3 и 2 из таблицы 4. В левый столбец выпишем значения  – прироста прибыли четвертого предприятия от объема инвестиций.
– прироста прибыли четвертого предприятия от объема инвестиций.
Так как по условию задачи в четыре предприятии вкладывается полный объем имеющихся средств, то в таблицу 5 мы заполним ячейки только на диагонали, соответствующей объему инвестиций Е = 700 млн. руб. заполним эти ячейки значениями сумм величин 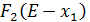 и
и 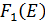 . на этой диагонали найдем максимальное значение, соответствующее оптимальному плану размещения инвестиций по четырем предприятиям.
. на этой диагонали найдем максимальное значение, соответствующее оптимальному плану размещения инвестиций по четырем предприятиям.
(Табл. 5)
| x1 |
E - x1 | 0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
|
F1(x1)/F2(E - x1)
| 0 | 61 | 111 | 141 | 163 | 187 | 206 | 224 | |
| 0 | 0 |
|
|
|
|
|
|
| 224 |
|
100 | 25 |
|
|
|
|
|
| 231 |
|
|
200 | 41 |
|
|
|
|
| 228 |
|
|
|
300 | 55 |
|
|
|
| 218 |
|
|
|
|
400 | 65 |
|
|
| 206 |
|
|
|
|
|
500 | 75 |
|
| 186 |
|
|
|
|
|
|
600 | 80 |
| 141 |
|
|
|
|
|
|
|
700 | 85 | 85 |
|
|
|
|
|
|
|
В таблице 5 наибольшее значение на диагонали для значения Е = 700 равно 231, таким образом максимальное значения суммарного прироста прибыли на всех предприятиях вместе, будет:
Zmax = 231 млн. руб.
Определим, при каком распределении вложенных средств по четырем предприятиям достигается это максимальное значение суммарного прироста прибыли. Рассмотрим шаги задачи и таблицы на этих шагах в обратном порядке.
Из таблицы 5 видно, что Zmax достигается при выделении первому предприятию инвестиций в размере 100 млн. руб., таким образом, в оптимальном решении:
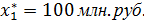
На долю остальных трех предприятий остается 600 млн. руб. Из таблицы 4 определим оптимальное распределение инвестиций в размере Е = 600 млн. руб. и долю этих инвестиций, приходящуюся на второе предприятие.
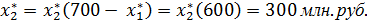
Таким образом, для обеспечения оптимального решения второе предприятие должно получить инвестиции в размере
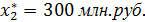 При этом размер инвестиций, приходящийся на предприятия 4 и 3, составит Е = 300 млн. руб. Продолжая обратный процесс, переходим к таблице 2 и найдем оптимальное распределение этих средств между предприятиями 4 и 3.
При этом размер инвестиций, приходящийся на предприятия 4 и 3, составит Е = 300 млн. руб. Продолжая обратный процесс, переходим к таблице 2 и найдем оптимальное распределение этих средств между предприятиями 4 и 3.
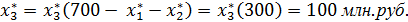
Оптимальный размер инвестиций, которых должно получить третье предприятие составляет 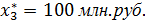 На долю четвертого предприятия, при этом остается:
На долю четвертого предприятия, при этом остается:
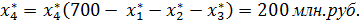
Проверим по данным исходной таблицы выполнение равенства:
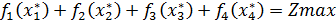
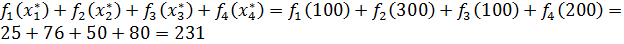 , равенство выполняется.
, равенство выполняется.
Ответ:
Наилучшим является следующее распределение капитальных вложений по предприятиям:
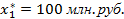 ,
, 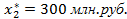 ,
, 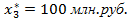 ,
, 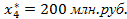
Оно обеспечивает производственному объединению наибольший возможный прирост прибыли Zmax = 231 млн. руб.
Пр.10 «Нахождение кратчайших путей в графе. Алгоритм Дейкстры»
Цель:
Приобретение навыков нахождения кратчайших путей в графе с помощью алгоритма Дейкстры.
Вариант 10.

Изобразим граф с указанием числовых значений весов дуг и направлением ориентации рёбер. 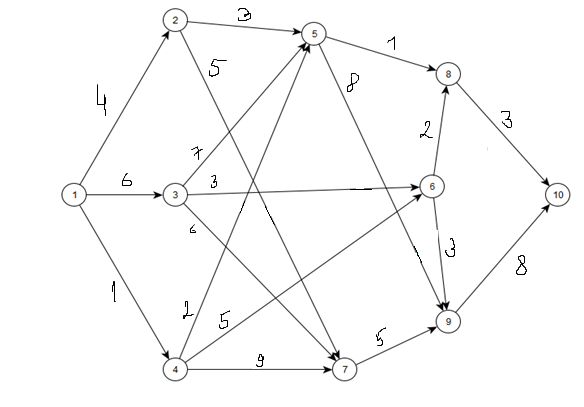 С помощью алгоритма Дейкстры найдем длины наименьших путей, а также массив вершин предшественников на путях, из источника I – вершины 1 до каждой другой вершины графа, а также до стока – вершины 10.
С помощью алгоритма Дейкстры найдем длины наименьших путей, а также массив вершин предшественников на путях, из источника I – вершины 1 до каждой другой вершины графа, а также до стока – вершины 10.
Для этого нам понадобиться выполнить 9 итераций алгоритма
Вершины, включенные в S на каждом шаге, будем помечать желтым цветом (рис. 1), пути до вершин, которые возможно определить на текущем шаге алгоритма – зеленым, путь минимальной длинны на данном шаге – красным. Недоступные пути – синим.
Шаг 1.
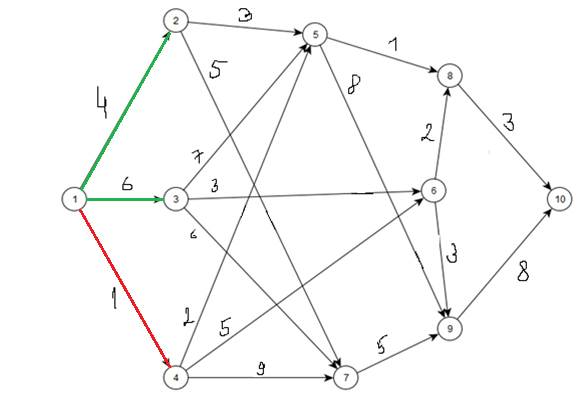

Табл. 1.
Шаг 2.
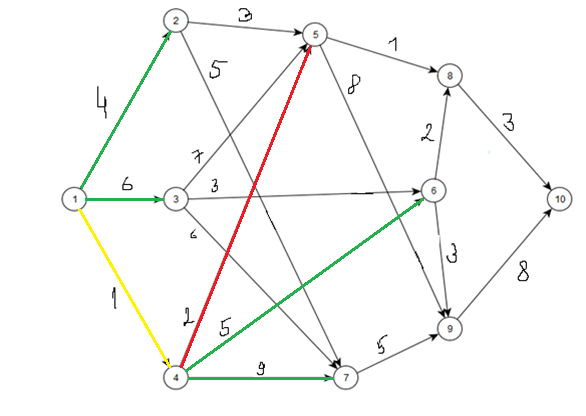

Табл. 2.
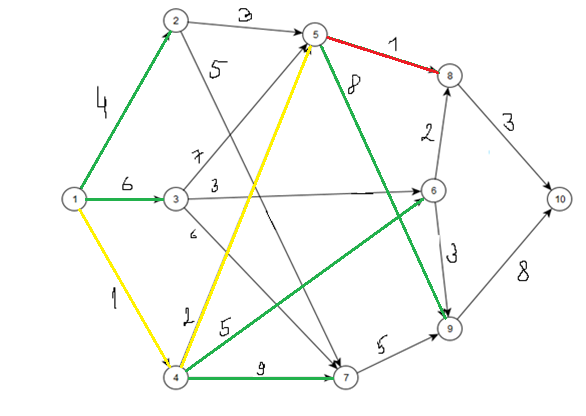

Табл. 3.
Шаг 4.
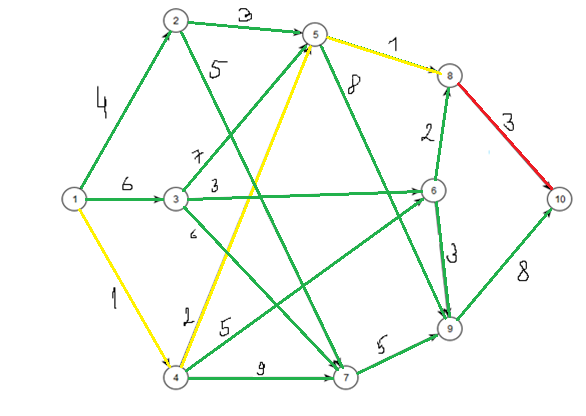
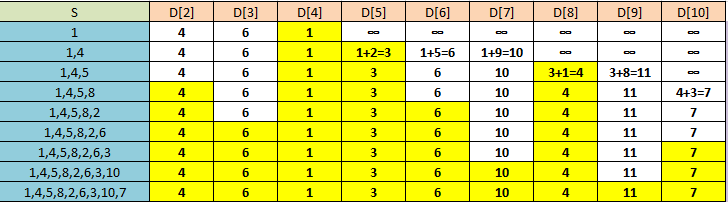
Табл. 4.
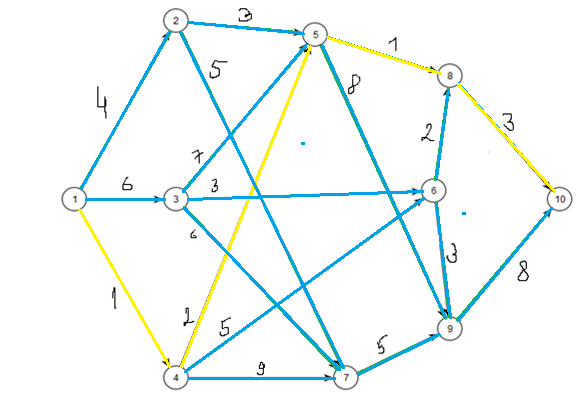

Кратчайший путь пути от источника – вершины 1 до стока – вершины 10 будет равен: D[10] = 7 проходит через вершины 1 -> 4 -> 5 -> 8 -> S
|
|
Переменные задачи
Для получения математической модели задачи введем неотрицательные целочисленные переменные 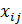 соответствующие дугам графа, где i – индекс вершины, являющейся началом дуги, j – индекс вершины, являющейся концом дуги, которые интерпретируются как величина потока по дуге (i, j). Количество переменных определяется количеством дуг в графе.
соответствующие дугам графа, где i – индекс вершины, являющейся началом дуги, j – индекс вершины, являющейся концом дуги, которые интерпретируются как величина потока по дуге (i, j). Количество переменных определяется количеством дуг в графе.
Согласно графу из условия задачи, у нас будут 18 переменных, соответствующих дугам графа, обозначим их следующим образом:
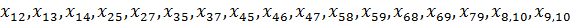
Ограничения
На переменные задачи накладываются условия не отрицательности и цело численности потока 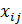 по дуге (i, j).
по дуге (i, j).
Математически это ограничение в общем виде можно записать следующим образом:
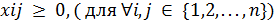
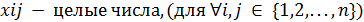
Для графа из условия задачи, данные ограничения будут:
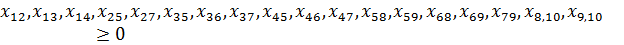
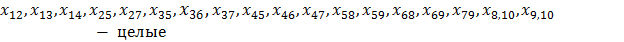
Условия наличия истока I в вершине 1 и стока S в вершине 10 накладывают на задачу соответствующие ограничения.
Величина потока из истока I в вершине 1 должна быть равна величине потока, пришедшего в сток S – вершину 10. В общем виде математически данное ограничение можно записать следующим образом:
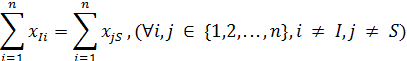
По условию задачи из вершины 1 выходят дуги (1, 2), (1, 3) и (1, 4), следовательно, величина потока из истока равна сумме потоков по этим ребрам:
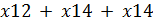
В вершину 6 поток приходит по ребрам (8, 10) и (9, 10), следовательно, величина потока из истока равна сумме потоков по этим ребрам:
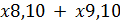
Из условия (1) получаем ограничение:
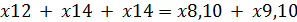
Величина потока по ребру не может быть больше пропускной способности ребра. Обозначив через 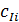 пропускную способность по ребру (i, j) в направлении от вершины i к вершине j, это ограничение в общем можно записать следующим образом:
пропускную способность по ребру (i, j) в направлении от вершины i к вершине j, это ограничение в общем можно записать следующим образом:
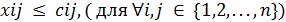
Для графа из условия задачи, данные ограничения будут:
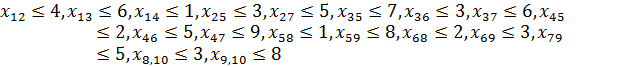
Последнее ограничение задачи заключается в том, чтобы для каждой вершины сети (кроме истока и стока) суммарный поток, входящий в вершину, был равен суммарному выходящему из вершины.
Математически это условие можно записать так:
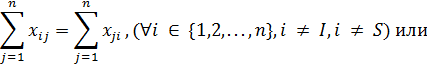
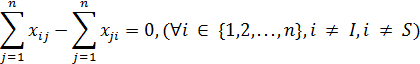
где I – индекс вершины-истока, S – индекс вершины-стока
Для графа из условия задачи имеем 8 вершин, не являющихся истоком или стоком, для каждой из них получим следующие ограничения:
Для вершины 2: 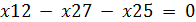
Для вершины 3: 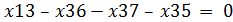
Для вершины 4: 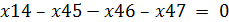
Для вершины 5: 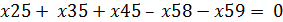
Для вершины 6: 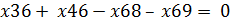
Для вершины 7: 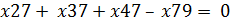
Для вершины 8: 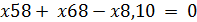
Целевая функция
По условию задачи необходимо найти максимальный поток по сети, который равен количеству вещества, вытекающего из истока I.
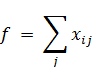
Где: j – конечные вершины ребер, исходящих из I;
Линейную функцию f называют мощностью потока сети, будем искать ее максимум.
Запишем математическую формулировку (в виде ЗЛП) задачи для условий, изображенных на графе:
Найти максимум целевой функции:
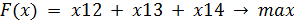
При ограничениях:
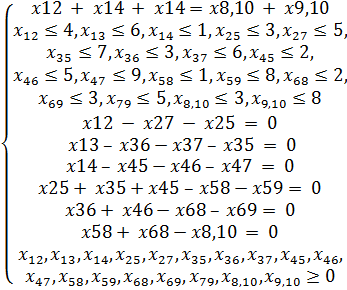
Задача 1.
Система может находиться в одном из пяти состояний (1, 2, 3, 4, 5).
Дана матрица Р вероятностей перехода системы из состояния в состояние за один шаг.
Постройте размеченный граф состояний системы, соответствующий матрице Р.
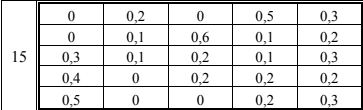
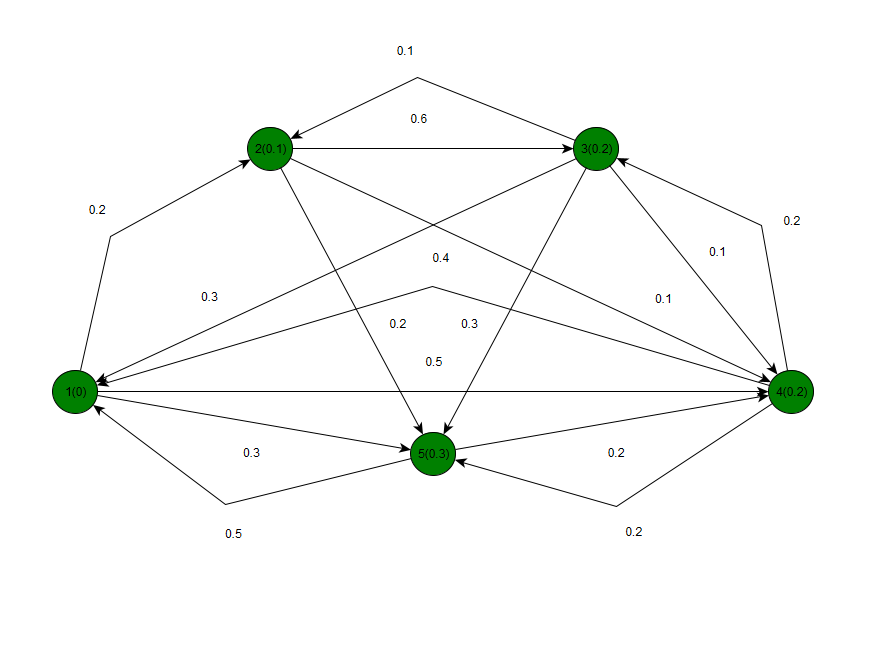
Задача 2.
Система может находиться в одном из четырех состояний (1, 2, 3, 4)
Переходы между состояниями за один цикл осуществляются с вероятностями заданными
матрицей P.

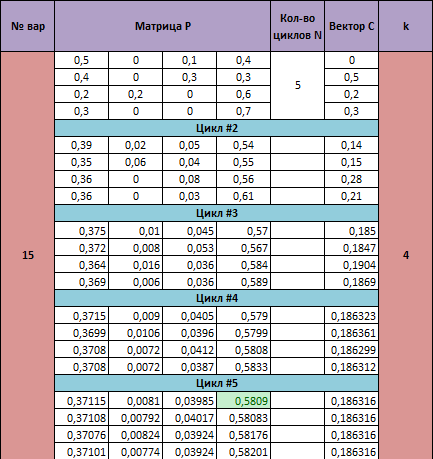
1) Определите матрицу вероятностей переходов за N циклов
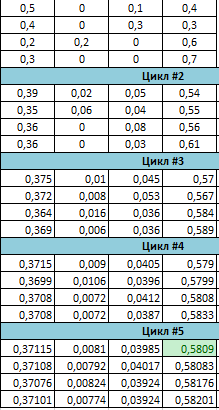
2) Распределение вероятностей состояний за N циклов, если начальное
распределение задается вектором С

3) Вероятность того, что через N циклов система будет в состоянии k, если в
начальный момент времени она находилась в состоянии 1.
Задача 1.
Составить систему дифференциальных уравнений Колмогорова, для непрерывной Марковской цепи, характеризующейся графом состояний из первого задания Практической работы №12.
Вариант №6
Начертим размеченный граф состояний, соответствующий матрице P.

Рис.1
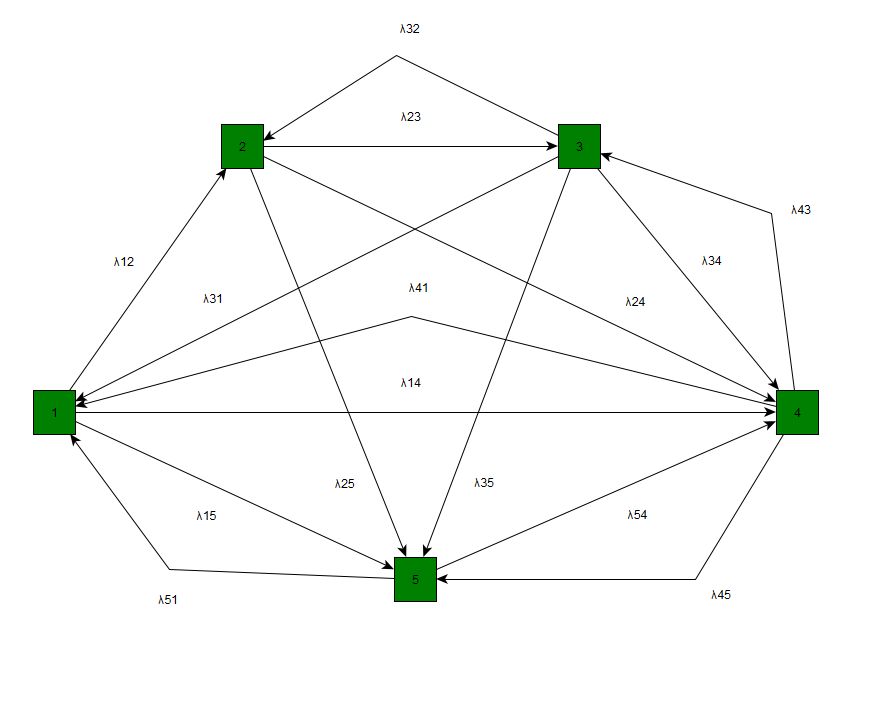
Рис.2
Размеченным графом будем считать такой граф, у которого стрелками указаны переходы из одного состояния в другое, а рядом со стрелкой указана интенсивность перехода. Будем различать 2 интенсивности – прямую λ, и обратную u.
Тогда 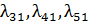 - интенсивности потоков отказов соответственно первого узла, а
- интенсивности потоков отказов соответственно первого узла, а 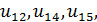 - соответственно интенсивности потоков возвратов узлов.
- соответственно интенсивности потоков возвратов узлов.
На основе построенного размеченного графа создадим математическую модель.
Наше техническое устройство в соответствии с построенным графом в любой момент времени будет находиться в одном из восьми возможных состояний. Обозначим вероятность каждого i-го состояния как pi(t), тогда
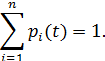
Для определения вероятности каждого состояния технического устройства составим соответствующие дифференциальные уравнения:
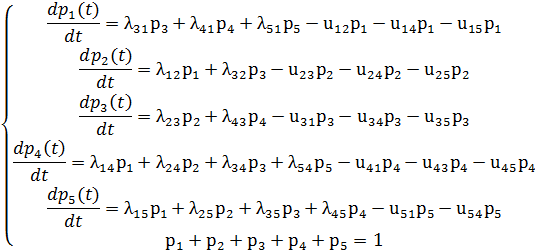
Задача №2
Техническое устройство состоит из 3узлов и в любой момент времени может находиться в одном из состояний.
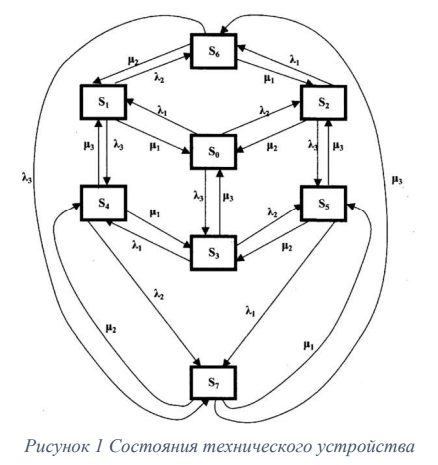
Численные значения интенсивности потоков событий: 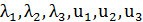 по вариантам даны в таблице.
по вариантам даны в таблице.
Вариант 26.
Дана система, которая может находиться в одном из пяти состояний. Система работает по схеме процесса гибели и размножения, граф которого показан на рисунке Рис. 1

Рис.1
Числовые значения интенсивности перехода системы из состояния в состояние заданы в таблице 1.
(Табл. 1)
| λ12 | λ23 | λ34 | λ45 | λ21 | λ32 | λ43 | λ54 |
| 1 | 1 | 1 | 5 | 1 | 5 | 1 | 5 |
Решение:
Вычислим финальные вероятности событий. Составим систему линейных уравнений:
для первого состояния S1 имеем:
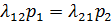 (1.1)
(1.1)
для второго состояния S2 суммы членов, соответствующих входящим и выходящим стрелкам, равны:
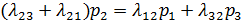
Но, в силу (1.1), можно сократить справа и слева равные друг другу члены 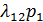 и
и 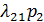 и получим:
и получим:
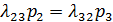
Так же для события S3:
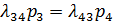
для события S4:
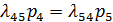
и для события S5:
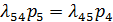
Итак, предельные вероятности 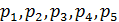 в этой схеме гибели и размножения удовлетворяют уравнениям и нормировочному условию:
в этой схеме гибели и размножения удовлетворяют уравнениям и нормировочному условию:
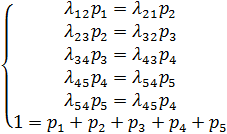
Решим эту систему уравнений. Будем решать эту систему следующим образом:
из первого уравнения выразим p2:
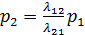 (1.2)
(1.2)
из второго, с учетом (1.2), получим:
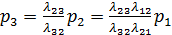 (1.3)
(1.3)
из третьего, с учетом (1.3), получим:
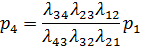
из четвертого, с учетом предыдущего, получим:
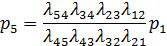
Подставим вероятности в нормировочное условие:
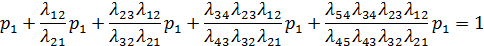
Получаем
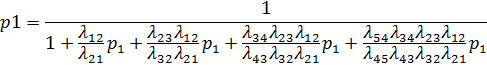
Вставим числовые значения в формулу:
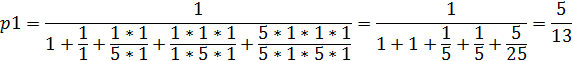
Остальные вероятности выражаются через 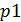 :
:
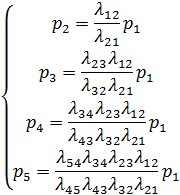
Подставим числовые значения:
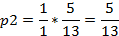
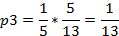
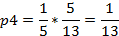
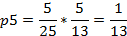
Проверим правильность вычислений, подставив найденные значения предельных вероятностей в нормировочное условие:
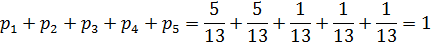
Вариант 15.
На вход системы, имеющей 9 терминалов обслуживания заявок, поступают заявки с интенсивностью λ = 2. Среднее время обслуживания заявки равно T = 3. Если терминалы заняты, то заявка встает в очередь.
Дана таблица с номерами характеристик многоканальной СМО

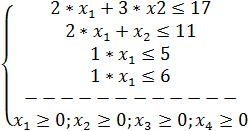
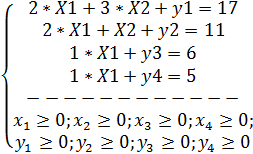
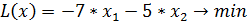
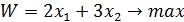
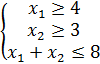
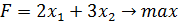
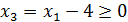
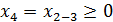
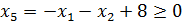

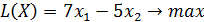 ,
,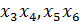 - свободные переменные
- свободные переменные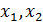 - базисные переменные (зависят от свободных)
- базисные переменные (зависят от свободных)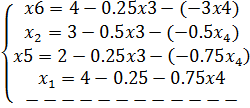
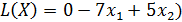
 Решение:
Решение: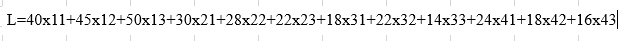
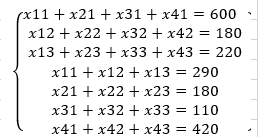
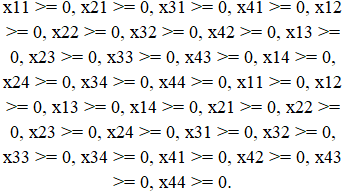
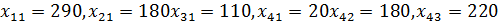
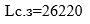
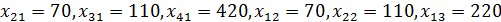
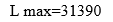
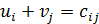
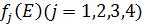 . Значения этих функций
. Значения этих функций 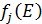 известны и для каждого варианта записаны в таблице ниже в след. виде:
известны и для каждого варианта записаны в таблице ниже в след. виде: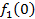
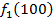
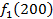
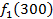
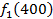
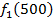
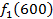
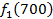
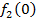
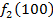
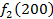
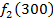
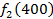
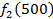
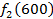
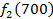
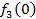
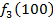
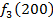
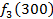
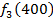
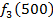
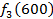
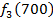
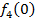
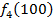
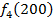
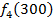
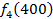
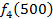
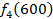
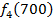
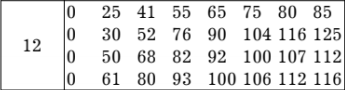
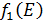 от объема вложений Е на четвертом предприятии определяется верхней строкой таблицы исходных данных.
от объема вложений Е на четвертом предприятии определяется верхней строкой таблицы исходных данных.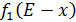 . В левый столбец выпишем значения
. В левый столбец выпишем значения 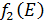 - прироста прибыли третьего предприятия от объема инвестиций.
- прироста прибыли третьего предприятия от объема инвестиций.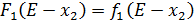 , и заносим в таблицу. Каждая северо-восточная диагональ этой таблицы определяет возможные значения суммарного прироста прибыли от различных вариантов распределения определенного объема инвестиций между двумя предприятиями. На каждой северо-восточной диагонали находим наибольшее число (которое выделяем жирным).
, и заносим в таблицу. Каждая северо-восточная диагональ этой таблицы определяет возможные значения суммарного прироста прибыли от различных вариантов распределения определенного объема инвестиций между двумя предприятиями. На каждой северо-восточной диагонали находим наибольшее число (которое выделяем жирным).


