
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Конечные элементы высших порядков
Рассмотренный в пункте 12.34 треугольный КЭ - элемент постоянной деформации. Если распределение перемещений описывают линейные функции (12.93), то компоненты деформации постоянны в пределах элемента (не зависят от координат):
Во всех точках элемента значения любой компоненты деформации и напряжения одинаковы, при переходе к соседнему элементу они меняются скачкообразно. Поле перемещений на границе элементов непрерывное, а поле деформаций имеет разрыв. Можно предложить два пути повышения точности: 1. Измельчение элементов. Этот путь - простой и универсальный, но ведет к увеличению числа уравнений и резкому росту вычислительных затрат. Если число неизвестных 2. Усложнение элементов позволяет получить ту же точность при меньшем числе узлов. Если применять для аппроксимации полиномы высокого порядка, коэффициентов в них будет больше, и в каждом элементе должно быть больше узлов. Добавление еще трех узлов в линейный треугольный конечный элемент (переход к квадратичному элементу) дает более высокую точность, чем разбиение данного КЭ на четыре линейных элемента. Этот путь ведет к усложнению работы программиста (практически он берет часть вычислений компьютера на себя). Проблемы возрастают при нелинейности, например при текучести. Элемент постоянной деформации переходит в пластическое состояние сразу весь, а сложный элемент может иметь упругие и пластические части. В этом случае несколько простых элементов, возможно, дадут более высокую точность, чем один сложный. Таким образом, сложные методы решения дают максимальный эффект при решении простых задач. Они нацелены на отыскание в решаемой задаче простоты и ее использование в целях экономии времени счета и памяти компьютера. Общее правило: выбирать простейший из пригодных для данной модели тип КЭ. Линейный КЭ плохо работает в условиях текучести у концентраторов напряжения. Волокна материала в этой зоне под нагрузкой сильно изгибаются, а жесткие границы линейных КЭ плохо воспроизводят этот изгиб. В элементах появляются «помехи» - ложные деформации изменения объема и гидростатические напряжения. Границы квадратичного КЭ могут изгибаться, при этом погрешность резко сокращается.
Можно рекомендовать восьмиузловой элемент для двумерных задач и двадцатиузловой - для объемных. Суперэлементы Один из методов решения системы МКЭ называется фронтальным. Дело в том, что для исключения первого неизвестного при решении системы уравнений методом Гаусса нужны не все уравнения, а только несколько первых, в которые данное неизвестное входит. Поэтому составление и решение системы могут идти параллельно: двигаясь фронтом по модели, мы составляем часть системы уравнений и тут же исключаем часть неизвестных. Метод позволяет сэкономить память и время счета. Та же идея заложена в применение суперэлементов, которые представляют собой элементы высокого порядка, собранные из более простых. Составляем частично систему уравнений для отдельного участка модели. Исключение неизвестных начинаем с внутренних узлов участка, оставляя узлы на границе этого участка с остальной частью модели. После этой операции получаем суперэлемент для этого участка с узлами только на границе, но с такими же параметрами жесткости, как у исходной совокупности большого числа элементов, содержащихся внутри. Проделав такую операцию с каждым участком, можно затем собрать из этих суперэлементов всю модель и исключить оставшиеся неизвестные. Общее число операций при этом такое же, но на каждом этапе как бы решается система уравнений меньшего размера. Экономия возможна, если имеется большое число одинаковых суперэлементов. Тогда операция исключения внутренних неизвестных для них проводится один раз. Если зона пластических деформаций невелика, выгодно превратить в суперэлемент упругую часть модели. Наиболее полезны суперэлементы для моделирования сварочных процессов. Всю зону сварки можно разбить на одинаковые секции в направлении оси шва и заменить суперэлементами, что позволяет сэкономить память при решении сложных задач.
12.39. Изопараметрическое преобразование при построении КЭ Существуют следующие виды КЭ: - субпараметрические – элементы, в которых полиномы, описывающие внутреннее состояние элемента (температуру, перемещения), имеют порядок ниже, чем описывающие геометрическую форму элемента; - изопараметрические (наиболее распространенные) - позволяют использовать одинаковые функции при построении элемента и при работе с ним; - суперпараметрические - элементы, в которых внутреннее состояние элемента описывают полиномы более высокого порядка. Каждая из функций формы (ФФ) конечного элемента обращается в единицу в одном из его узлов и в нуль – в остальных, при этом в каждой точке КЭ сумма всех ФФ равна единице. Для квадратичного элемента сложной формы с большим количеством узлов вывести уравнения для таких функций непросто. Выход в том, что уравнения составляют для простого элемента, который является моделью сложного. Рассмотрим пример четырехугольного элемента с восемью узлами (рис. 12.29).
Рис. 12.29. Изопараметрическое преобразование: А – КЭ, В – его модель.
На рис. 12.29 справа изображен элемент А в глобальной системе координат Вначале обеспечим условия равенства нулю. ФФ Подставив координаты узла 2:
Для угловых узлов функции немного другие:
Эти ФФ будут годны не только для модели, но и для самого КЭ, если мы найдем способ установить однозначное соответствие между точками элемента и его модели. Переход от В к А простой. Если даны локальные координаты
Если точка В совпадает с одним из узлов, например, с узлом 3, то для нее Обратный переход от А к В гораздо сложнее, поэтому весь алгоритм устроен так, чтобы переходить только от В к А. Перейти от А к В достаточно просто в случае одномерного (стержневого) квадратичного элемента. Изопараметрическое преобразование можно использовать для разбиения построенного КЭ на более мелкие. Разбиение производят на модели КЭ, а затем по локальным координатам узлов полученных мелких элементов рассчитываются глобальные координаты этих узлов. Чтобы обеспечить стыковку создаваемых сеток в смежных элементах, целесообразно вначале разбить на части их общие ребра, затем общие грани между ребрами, а затем уже - внутренние объемы между гранями. Разбиение пространственных искривленных пластин производится так же, как и разбиение плоских пластин. Модель остается прежней (см. рис. 12.29), ФФ вычисляют по тем же формулам, но каждый узел КЭ имеет три глобальных координаты
Этот подход может быть распространен на разбиение объемного КЭ. Вначале разбиваем ребра, размещая на них дополнительные узлы. Затем разбиваем грани. Поскольку на ребрах по контуру грани все узлы размещены, эта задача сводится к разбиению пространственной пластины. После этого на каждой грани появляются линии сетки с узлами на них. Четыре такие линии, по одной с каждой грани, образуют четырехугольник, который можно разбить таким же образом, как и грань. Для расчета деформаций необходимо вычисление градиентов (производных функций формы по одной из координат):
Поскольку ФФ выражена в локальных координатах
где
или
|
|||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 133; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.246.203 (0.014 с.) |
 .
.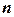 , то объем памяти для матрицы жесткости пропорционален
, то объем памяти для матрицы жесткости пропорционален  , а число операций для решения системы уравнений и время счета пропорциональны
, а число операций для решения системы уравнений и время счета пропорциональны  . К тому же такие простые элементы увеличивают жесткость модели по сравнению с реальной, поскольку их границы остаются прямыми (не могут искривляться).
. К тому же такие простые элементы увеличивают жесткость модели по сравнению с реальной, поскольку их границы остаются прямыми (не могут искривляться).
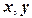 , а слева – его модель В в локальных координатах
, а слева – его модель В в локальных координатах 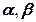 . Начало локальных координат – в центре элемента, диапазон их изменения от -1 до 1. Модель имеет вид квадрата размером 2х2, все локальные координаты узлов равны -1, 0 или 1. Стороны самого конечного элемента являются квадратными параболами, координаты всех восьми узлов могут быть любыми.
. Начало локальных координат – в центре элемента, диапазон их изменения от -1 до 1. Модель имеет вид квадрата размером 2х2, все локальные координаты узлов равны -1, 0 или 1. Стороны самого конечного элемента являются квадратными параболами, координаты всех восьми узлов могут быть любыми. для узла 2 должна быть равна нулю в точках 1, 3, 4, 5, 6, 7 и 8. Это можно обеспечить, задав
для узла 2 должна быть равна нулю в точках 1, 3, 4, 5, 6, 7 и 8. Это можно обеспечить, задав  . Первая из них обращается в нуль в узлах 1, 7, 8, вторая - в узлах 3, 4, 5, а третья в узлах 5, 6, 7.
. Первая из них обращается в нуль в узлах 1, 7, 8, вторая - в узлах 3, 4, 5, а третья в узлах 5, 6, 7. , получим
, получим 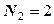 . Значит, формулу нужно изменить:
. Значит, формулу нужно изменить: 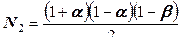 . Аналогично:
. Аналогично: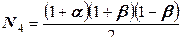 ,
, 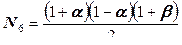 ,
,  .
. ,
, 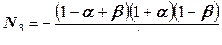 ,
,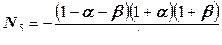 ,
, 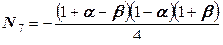 .
. точки модели В, то можно найти значения ФФ для этой точки и вычислить глобальные координаты точки А по формулам:
точки модели В, то можно найти значения ФФ для этой точки и вычислить глобальные координаты точки А по формулам: ,
,  ,
, 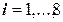 . (12.112)
. (12.112)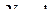 , а остальные ФФ равны нулю. Тогда, согласно (12.112), координаты точки А совпадут с координатами
, а остальные ФФ равны нулю. Тогда, согласно (12.112), координаты точки А совпадут с координатами  точки 3.
точки 3.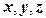 , и изопараметрическое преобразование осуществляется по формулам:
, и изопараметрическое преобразование осуществляется по формулам: ,
, 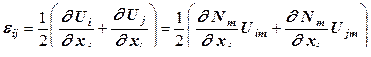 . (см. (12.97))
. (см. (12.97)) , ее производная по глобальной координате
, ее производная по глобальной координате  :
: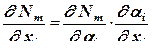 , (12.114)
, (12.114)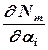 – градиент для модели элемента;
– градиент для модели элемента; 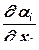 – якобиан (матрица Якоби, матрица искажения пространства). Если модель полностью совпадает с элементом, то
– якобиан (матрица Якоби, матрица искажения пространства). Если модель полностью совпадает с элементом, то  , если она отличается от него только масштабным множителем, то
, если она отличается от него только масштабным множителем, то 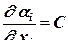 . Если же элемент криволинейный, то в каждой его точке своя матрица перехода размером
. Если же элемент криволинейный, то в каждой его точке своя матрица перехода размером  (для плоского КЭ)
(для плоского КЭ)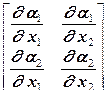 (12.115)
(12.115)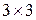 (для объемного КЭ). Чтобы вычислить якобиан, нужно составить матрицу
(для объемного КЭ). Чтобы вычислить якобиан, нужно составить матрицу  , а затем найти обратную матрицу
, а затем найти обратную матрицу 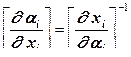 . Весь алгоритм построен так, что мы двигаемся только от В к А (см. рис. 12.29).
. Весь алгоритм построен так, что мы двигаемся только от В к А (см. рис. 12.29).


