Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Введение в циклические коды.
Циклические коды относятся к классу линейных систематических кодов. Они названы циклическими потому, что циклический сдвиг разрешенной кодовой комбинации приводит также к разрешенной комбинации. Например, если Сущность циклической перестановки заключается в том, что крайний левый символ кодовой комбинации (символ старшего разряда) занимает место первого, первый – второго и т.д. до тех пор, пока предпоследний символ не займет место последнего. Запишем совокупность кодовых комбинаций, получающихся циклическим сдвигом n -разрядной кодовой комбинации, например пятиразрядной 10011: 10011, 00111, 01110, 11100, 11001. При работе с циклическими кодами принято кодовые комбинации
где x – основание системы счисления; bi – цифры данной системы счисления. Для двоичной системы счисления x =2, а bi равны 0 или 1. Например, двоичную последовательность 010101 можно представить в виде многочлена
Представление кодовых комбинаций в виде многочленов позволяет установить однозначное соответствие между ними и свести действия над кодовыми комбинациями к действиям над многочленами. Над многочленами можно производить все алгебраические действия. Следует заметить, что при работе с двоичными многочленами сложение осуществляется по модулю два.
Пример 1. Рассмотрим действия над двоичными многочленами. Сложение двоичных многочленов сводится к сложению по модулю два коэффициентов при равных степенях переменной x:
При сложении по модулю два 1+1=0, x + x = 0, x 2 + x 2 = 0 и т.д. Умножение осуществляется по обычному правилу умножения степенных функций, при этом коэффициенты при равных степенях складываются по модулю два:
Деление также производится, как обычное деление многочленов, однако операция вычитания заменяется операцией сложения по модулю два (сложение и вычитание по модулю два дают один и тот же результат):
Вышеупомянутый циклический сдвиг некоторого многочлена соответствует простому умножению на x. Умножив, например, многочлен x 3 + x 2 + 1, соответствующий комбинации 001101, на x, получим многочлен x 4 + x 3 + x, соответствующий комбинации 011010. Циклические коды характеризуются тем, что многочлены разрешенных кодовых комбинаций B (x) делятся без остатка на так называемый порождающий (образующий) многочлен P (x). Порождающим многочленом может быть любой многочлен P (x) степени r = n - k, который делит без остатка двучлен xn +1. Например, порождающий многочлен x 2 + x +1 делит без остатка двучлен x 6 +1, а многочлен x 3 + x +1 делит двучлен x 7 +1. В теории циклических кодов доказывается, что наилучшими свойствами обладают коды с порождающими многочленами в виде неприводимых (примитивных) многочленов. Такие многочлены, как и простые числа, делятся только на себя и единицу. Некоторые неприводимые многочлены приведены в табл.1. Таблица 1.
При этом количество не повторяющихся остатков от деления на образующий полином должно быть не менее чем
Как видно и в первом и во втором случае имеется семь не повторяющихся остатков от деления, следовательно, можно использовать оба полинома в качестве образующего многочлена. Полином P (x) = x 3 + x 2 + 1 является образующим многочленом циклического кода Хэмминга (7,4) для исправления одной ошибки. Процесс циклического кодирования сводится к отысканию многочлена B (x) по известным многочленам A (x) и P (x), который бы делился на P (x) без остатка. Здесь A (x) – многочлен степени k -1, соответствующий информационной последовательности символов. Очевидно, что правило построения циклического кода можно представить в виде произведения информационной кодовой комбинации на порождающий многочлен:
Пример 2. Дана кодовая комбинации 0111. Построить разрешенную кодовую комбинацию циклического кода (7,4). Так как, число информационных элементов известно (k =4), то число проверочных элементов r = n - k =3. По таблице порождающих многочленов (табл.1) при r =3 выбираем любой многочлен (один из двух). Пусть P (x)= x 3 + x +1. Представляем кодовую комбинацию 0111 в виде многочлена: A (x)= x 2 + x +1. Умножаем A (x) на порождающий многочлен P (x) B(x)=(x2+x+1)(x3+x+1)=x5+x4+1. Записываем полученный многочлен B(x) в виде разрешенной кодовой комбинации: 0 1 1 0 0 0 1.
Порождающий многочлен P (x)= x 3 + x +1 Таблица 2
В табл.2 приведены все возможные информационные кодовые комбинации длиной n =4 и соответствующие им разрешенные кодовые комбинации циклического кода (7,4), полученные на основании (1). Из таблицы видно, что разрешенные кодовые комбинации обладают циклическим свойством. Например, циклический сдвиг разрешенной кодовой комбинации 0001011 (комбинация под №1) приводит также к разрешенной комбинации 0010110 (комбинация под №12), а их инвертированные копии комбинация под №13 к комбинация под №15.
Однако полученный таким способом циклический код является неразделимым, поскольку информационные и проверочные символы разрешенных кодовых комбинаций оказываются перемешанными, что затрудняет процесс декодирования. На практике применяется другой способ нахождения многочлена B (x), а именно B (x)= A (x) xr + R (x), (2) где R (x) – остаток от деления произведения A (x) xr на порождающий многочлен P (x). Результат такого деления можно представить в виде
Здесь Q (x) – частное от деления. Построение разрешенных кодовых комбинаций данным способом сводится к следующему: 1. Представляем информационные кодовые комбинации длиной k в виде многочленов A (x);
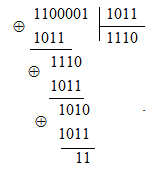
2. Умножаем A (x) на одночлен xr, т.е. осуществляем сдвиг кодовой комбинации на r разрядов; 3. Делим A (x) xr на порождающий многочлен P (x) степени r (табл.1), чтобы получить остаток R (x); 4. Добавляем R (x) к A (x) xr; 5. Представляем многочлен B (x)= A (x) xr + R (x) в виде кодовой комбинации. Этот способ кодирования широко применяется на практике. Пример 3. Построим разрешенную кодовую комбинацию циклического кода (7,4), вышеуказанным способом. В качестве информационной кодовой комбинации возьмем кодовую комбинацию, рассмотренную в примере 2: 0111, и тот же порождающий многочлен P (x)= x 3 + x +1. Решение: 1. Записываем кодовую комбинацию 0111 в виде многочлена: A (x)= x 2 + x +1. 2. Умножаем A (x) на x 3 (так как r = 3): A (x) x 3 =(x 2 + x +1) x 3 = x 5 + x 4 + x 3. 3. Делим A (x) x 3 на порождающий многочлен P (x)
Таким образом, остаток от деления R (x)= x. 4. Получаем многочлен B(x)=A(x) xr+R(x)= x5+x4+x3+x. 5. Записываем его в виде разрешенной кодовой комбинации:
Проще оперировать с двоичными символами. 1. Производим сдвиг влево на r разрядов кодируемую комбинацию 0111000. 2. Делим полученную кодовую комбинацию на образующий полином
3. Вместо r разрядов записываем полученный остаток от деления 0111010. Видно, что в полученной кодовой комбинации можно выделить информационные и проверочные символы. В табл. 3 приведены разрешенные кодовые комбинации циклического кода (7,4), полученные на основании (2). Рассматривая этот код, можно увидеть, что он обладает циклическим свойством и является разделимым. Порождающий многочлен P (x)= x 3 + x +1 Таблица 3
Обнаружение ошибок при циклическом кодировании сводится к делению принятой кодовой комбинации на тот же порождающий многочлен, который использовался при кодировании. Если в принятой кодовой комбинации нет ошибок, то деление произойдет без остатка. Если при делении получится остаток, то это свидетельствует о наличии ошибки.
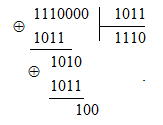
Пример 4. В качестве разрешенной кодовой комбинации возьмем кодовую комбинацию, полученную в примере 3: B(x)=x5+x4+x3+x (или в двоичном виде 0111010), а P (x)= x 3 + x +1 (в двоичном виде 1011). Допустим, что в принятой кодовой комбинации нет ошибок. Произведем ее деление на порождающий многочлен
Наличие нулевого остатка подтверждает, что в принятой кодовой комбинации нет ошибок. Теперь допустим, что произошла ошибка в старшем разряде. В этом случае кодовая комбинация имеет вид 1111010. Запишем принятую кодовую комбинацию в виде многочлена:
Остаток R (x)=x2+1 (или в двоичном виде 101) свидетельствует об ошибке в принятой кодовой комбинации.
Исправление ошибок при циклическом кодировании основано на анализе остатка R (x), полученного при делении принятой кодовой комбинации Следует отметить, что для всех разрешенных кодовых комбинаций ошибка на одной и той же позиции дает одинаковый остаток. Поэтому в принципе ошибки можно исправлять на основе таблицы соответствий между видом остатка и номером ошибочной позиции в кодовой комбинации. Однако свойство цикличности позволяет избавиться от запоминания в памяти декодера остатков для исправления ошибок и тем самым существенно упростить процедуру декодирования. Существует несколько методов декодирования циклических кодов. Один из методов исправления ошибок циклическим кодом осуществляют следующим образом: 1. Принятую кодовую комбинацию 2. Если в результате деления вес остатка g > t, то производят циклический сдвиг вправо принятой комбинации. Полученную комбинацию опять делят на P (x) и вычисляют вес остатка. Если вес нового остатка g 3. Если после второго деления вес нового остатка g > t, то процедуру циклического сдвига вправо, деления на P (x) и вычисления веса остатка продолжают до тех пор, пока не будет выполнено условие g Рассмотрим на конкретном примере процесс исправления одиночной ошибки в принятой кодовой комбинации.
Пример 5. Дан циклический (7,4)-код с порождающим многочленом P (x)= x 3 + x +1 (см. табл. 1). Предположим, что передана десятая комбинация 1010011, а под действием помех исказился третий справа символ (исказился проверочный символ), т.е. принята комбинация 1010111. Порождающему многочлену соответствует комбинация 1011. Разделив принятую комбинацию на порождающий многочлен
  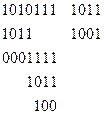 , ,
получим остаток 100, вес которого равен единице (g = 1). Складывая этот остаток по модулю 2 с принятой комбинацией
 , ,
получим исправленную комбинацию.
Пример 6. Рассмотрим более сложный случай. Предположим теперь, что в переданной десятой комбинации 1010011 произошла ошибка в пятом разряде (исказился информационный символ), т.е. принята комбинация 1000011. Делим эту комбинацию на порождающий многочлен
и получаем остаток 110, вес которого равен двум, т.е. g = 2 > t =1. Производим циклический сдвиг вправо этой комбинации и выполняем второе деление
Поскольку вес полученного остатка 11 также больше единицы, то выполняем второй циклический сдвиг и находим остаток от деления
Получили остаток 100, вес которого равен единице (g =1). Суммируем его с комбинацией 1110000
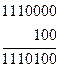 . .
Поскольку число выполненных сдвигов равно двум, то осуществляем обратный сдвиг комбинации 1110100 на два разряда влево и получаем исправленную кодовую комбинацию 1010011.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 1537; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.239.148 (0.059 с.) |
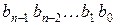 - разрешенная кодовая комбинация, тогда после ее циклической перестановки получим новую кодовую комбинацию
- разрешенная кодовая комбинация, тогда после ее циклической перестановки получим новую кодовую комбинацию 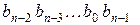 , которая также является разрешенной комбинацией циклического кода. Циклическое свойство этих кодов позволило упростить реализацию кодеров и декодеров и дало возможность в системах связи строить эффективные блочные коды большой длины с большим количеством разрешенных кодовых комбинаций. Цикл реализуют с помощью набора триггеров, объединенных в регистры сдвига.
, которая также является разрешенной комбинацией циклического кода. Циклическое свойство этих кодов позволило упростить реализацию кодеров и декодеров и дало возможность в системах связи строить эффективные блочные коды большой длины с большим количеством разрешенных кодовых комбинаций. Цикл реализуют с помощью набора триггеров, объединенных в регистры сдвига.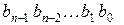 рассматривать в виде полиномов (многочленов) некоторой степени
рассматривать в виде полиномов (многочленов) некоторой степени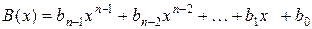 ,
,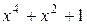 . Действительно,
. Действительно,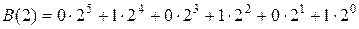 ;
;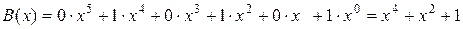 .
.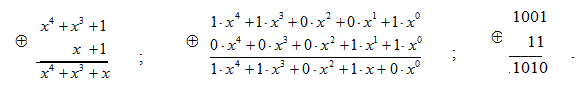
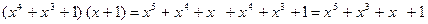 .
.
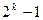 . Для этого произведем деление 10000000… но образующий полином
. Для этого произведем деление 10000000… но образующий полином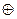
 . (1)
. (1)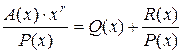 .
.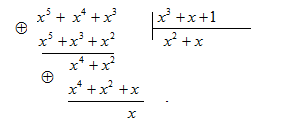
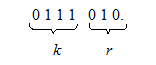

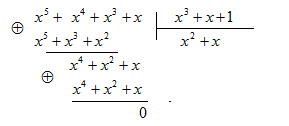

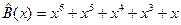 . Произведем операцию обнаружения ошибки
. Произведем операцию обнаружения ошибки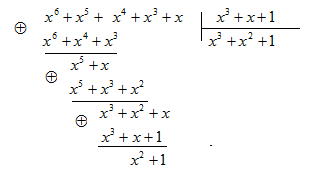

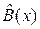 на порождающий полином P (x). Остаток R (x) называют также синдромом.
на порождающий полином P (x). Остаток R (x) называют также синдромом.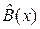 делят на порождающий многочлен P (x) и вычисляют вес остатка g, т.е. подсчитывают число единиц в остатке R (x). Если в результате деления вес g
делят на порождающий многочлен P (x) и вычисляют вес остатка g, т.е. подсчитывают число единиц в остатке R (x). Если в результате деления вес g 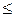 t (t – число исправляемых данным кодом ошибок), то принятую кодовую комбинацию складывают по модулю 2 с остатком, и она будет исправленной.
t (t – число исправляемых данным кодом ошибок), то принятую кодовую комбинацию складывают по модулю 2 с остатком, и она будет исправленной. t, то делимую комбинацию складывают по модулю 2 с остатком и полученную комбинацию циклически сдвигают влево на один разряд, что дает исправленную кодовую комбинацию.
t, то делимую комбинацию складывают по модулю 2 с остатком и полученную комбинацию циклически сдвигают влево на один разряд, что дает исправленную кодовую комбинацию.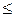 t. Как только это условие выполнится на некотором i -ом шаге, полученную комбинацию суммируют с остатком и производят обратный циклический сдвиг суммы на i -разрядов. В итоге получаем исправленную кодовую комбинацию.
t. Как только это условие выполнится на некотором i -ом шаге, полученную комбинацию суммируют с остатком и производят обратный циклический сдвиг суммы на i -разрядов. В итоге получаем исправленную кодовую комбинацию.