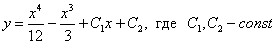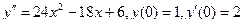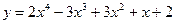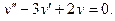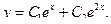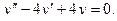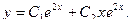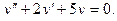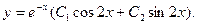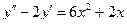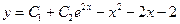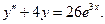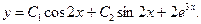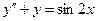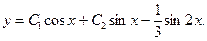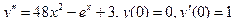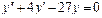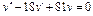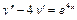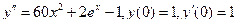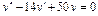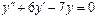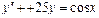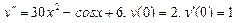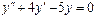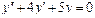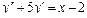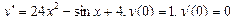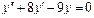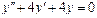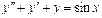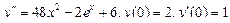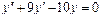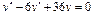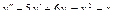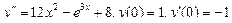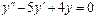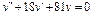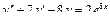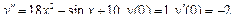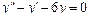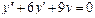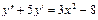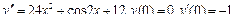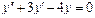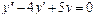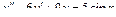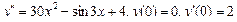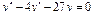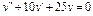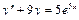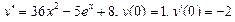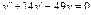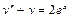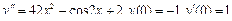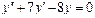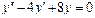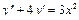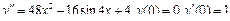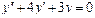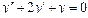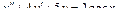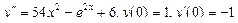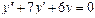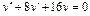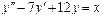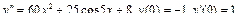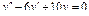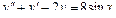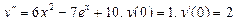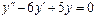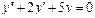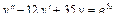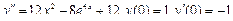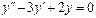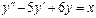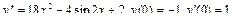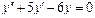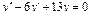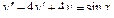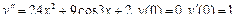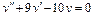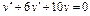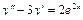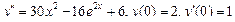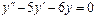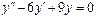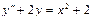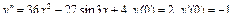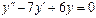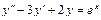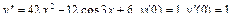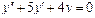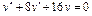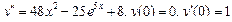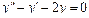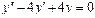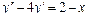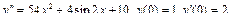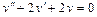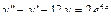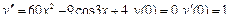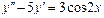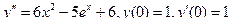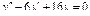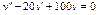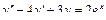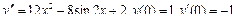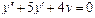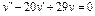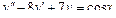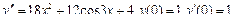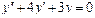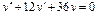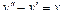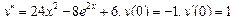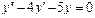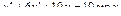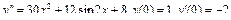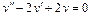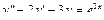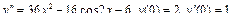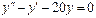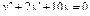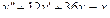Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Краткие теоретические сведения.
Понижение порядка дифференциального уравнения – основной метод решения уравнений высших порядков. Этот метод дает возможность сравнительно легко находить решение, однако, он применим далеко не ко всем уравнениям. Если f(x) – функция непрерывная на некотором промежутке a < x < b, то решение уравнения вида y( n) = f(x) может быть найдено последовательным интегрированием.
Уравнение Общая схема решения ЛОДУ приведена в таблице:
Линейное неоднородное уравнение второго порядка имеет вид: y''+ ρ x+qy = f (x) (3), где f (x) – непрерывная функция, отличная от нуля. Общее решение такого уравнения представляет собой сумму частного решения 1) Пусть правая часть имеет вид f (x)= e α x Pn (x), где Pn (x) – многочлен степени n. Тогда частное решение 2) Пусть правая часть имеет вид Пример 1. Найти общее уравнения y''–y' –2 y =0. Решение. Характеристическое уравнение имеет вид
Общее решение уравнения имеет вид y = C 1 e-x + C 2 e 2 x . Пример 2. Найти общее решение уравнения y'' –2 y' + y =0. Решение. Характеристическое уравнение имеет вид
Общее решение уравнения имеет вид y = ex (C 1+ C 2 x). Пример 3. Найти общее решение уравнения y'' –4 y' +13 y =0. Решение. Характеристическое уравнение имеет вид
Общее решение уравнения имеет вид y = e 2 x (C 1 cos3 x + C 2sin3 x). Пример 4. Найти общее решение уравнения y'' –2 y'+y = x 2+1. Решение. 1. Общее решение соответствующего однородного уравнения имеет вид yo = ex (C 1+ C 2 x) (см. пример 2).
2. Так как правая часть уравнения является многочленом второй степени и ни один из корней характеристического уравнения не равен нулю (e α x =0, α=0), то частное решение ищем в виде 3. Дифференцируем дважды
Подставляем 2 A– 4 Ax– 2 B+Ax 2 +Bx+C=x 2 + 1, Ax 2 + (B– 4 A) x+ 2 A– 2 B+C=x 2 + 1. Приравнивая коэффициенты при одинаковых степенях х в обеих частях равенства, имеем А =1, В -4 А =0, 2 А -2 В + С =1, Находим А =1, В =4, С =7. Итак, частное решение данного уравнения имеет вид Пример 5. Найти общее решение уравнения и частное решение, удовлетворяющее начальным условиям Решение. Общее решение соответствующего однородного уравнения имеет вид y o = C 1 ex + C 2 e –2 x (см. пример 1). В правой части данного уравнения стоит произведение многочлена нулевой степени на показательную функцию e α x при α=2. Так как среди корней характеристического уравнения нет корней, равных 2, то частное решение данного уравнения ищем в виде Дифференцируя дважды и подставляя в уравнение получаем:
Частное решение данного уравнения
Найдем частное решение, удовлетворяющее начальным условиям. Для этого продифференцируем у.
Подставляем начальные условия в у и у', находим С 1 и С 2:
Пример 6. Найти общее решение уравнения Решение. Характеристическое уравнение k 2+1=0 имеет корни k 1= i, k 2=- i. Поэтому общее решение соответствующего однородного уравнения будет y = C 1cos x + C 2sin x. В правой части тригонометрическая функция Пример 7. Найти общее решение дифференциального уравнения Решение: Понижаем степень уравнения до первого порядка Теперь интегрируем правую часть еще раз, получая общее решение:
Ответ: общее решение: Задания для совместного решения.
Задания для самостоятельного решения.
Занятие 11. Случайные величины
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-17; просмотров: 103; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.159.10 (0.016 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
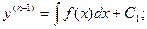
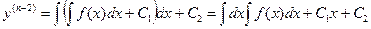 и т.д.
и т.д. Линейное однородное дифференциальное уравнение (ЛОДУ) второго порядка с постоянными коэффициентами имеет следующий вид: (1),где p и q – константы (числа), а в правой части – строго ноль.
Линейное однородное дифференциальное уравнение (ЛОДУ) второго порядка с постоянными коэффициентами имеет следующий вид: (1),где p и q – константы (числа), а в правой части – строго ноль.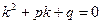 (2) называется характеристическим уравнением данного уравнения (1). Характеристическое уравнение (2) является квадратным уравнением, имеющим два корня. Обозначим их через k1 и k2.
(2) называется характеристическим уравнением данного уравнения (1). Характеристическое уравнение (2) является квадратным уравнением, имеющим два корня. Обозначим их через k1 и k2.
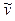 неоднородного уравнения (3) и общего решения yо соответствующего однородного уравнения (1):
неоднородного уравнения (3) и общего решения yо соответствующего однородного уравнения (1): 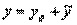 .
.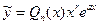 , где Qn (x) – многочлен той же степени, что и Pn (x) с неопределенными коэффициентами
, где Qn (x) – многочлен той же степени, что и Pn (x) с неопределенными коэффициентами 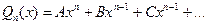 , а r – число, показывающее, сколько раз α является корнем характеристического уравнения (2).
, а r – число, показывающее, сколько раз α является корнем характеристического уравнения (2).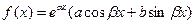 и α+β i, (α–β i) не является корнем характеристического уравнения. Тогда частное решение ищем в виде
и α+β i, (α–β i) не является корнем характеристического уравнения. Тогда частное решение ищем в виде 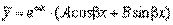 . Если же α+β i, (α–β i) является корнем характеристического уравнения, то частное решение находим в виде
. Если же α+β i, (α–β i) является корнем характеристического уравнения, то частное решение находим в виде 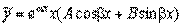 .
.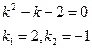
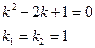
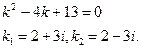
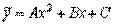 , где А, В, С – неизвестные коэффициенты.
, где А, В, С – неизвестные коэффициенты.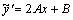

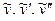 в данное уравнение, находим
в данное уравнение, находим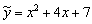 , а общее решение -
, а общее решение - 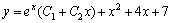 .
.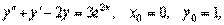
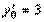 .
.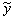 =A ∙ e 2 x .
=A ∙ e 2 x .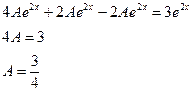
 и общее решение запишется в виде
и общее решение запишется в виде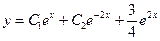
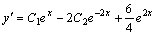 .
.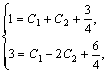
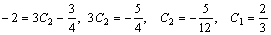 .
.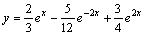 .
.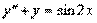 .
.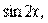 то есть a =0, b =1, β=2. Так как β=2 не является корнем характеристического уравнения, то частное решение надо искать в виде:
то есть a =0, b =1, β=2. Так как β=2 не является корнем характеристического уравнения, то частное решение надо искать в виде: 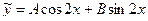 . Дифференцируя
. Дифференцируя 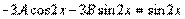 , откуда
, откуда 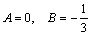 , т.е. частное решение
, т.е. частное решение 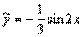 , а общее решение уравнения:
, а общее решение уравнения: 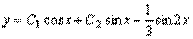 .
.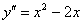
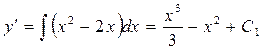
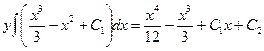 .
.