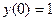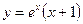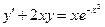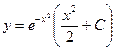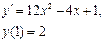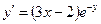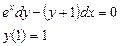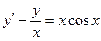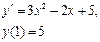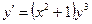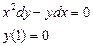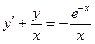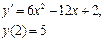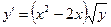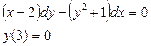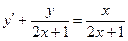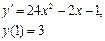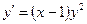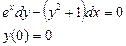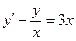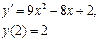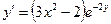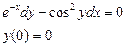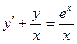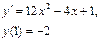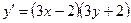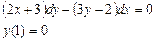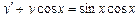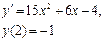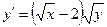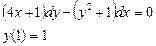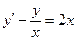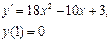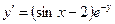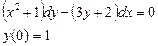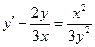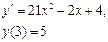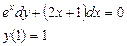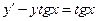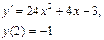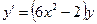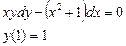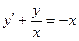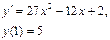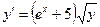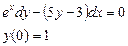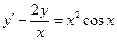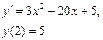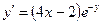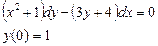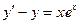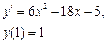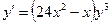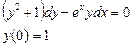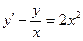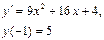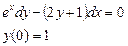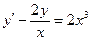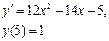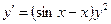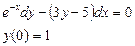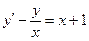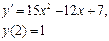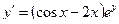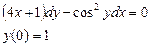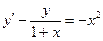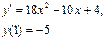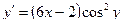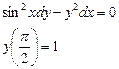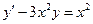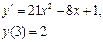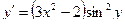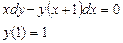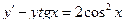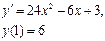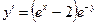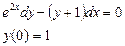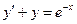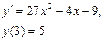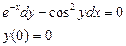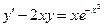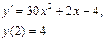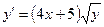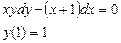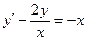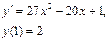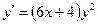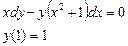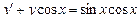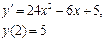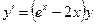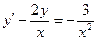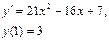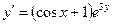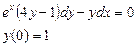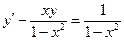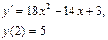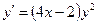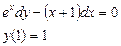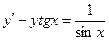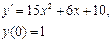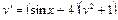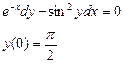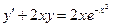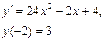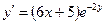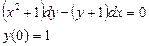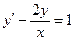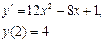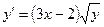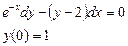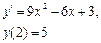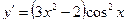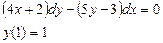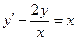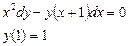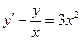Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Краткие теоретические сведения.
Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функции и производные (или дифференциалы) этой функции. Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения. Общим решением дифференциального уравнения называется такая дифференцируемая функция y = j(x, C), которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество. Решение вида у = j(х, С0) называется частным решением дифференциального уравнения. Задачей Коши (Огюстен Луи Коши (1789-1857)- французский математик) называется нахождение любого частного решения дифференциального уравнения вида у = j(х, С0), удовлетворяющего начальным условиям у(х0) = у0. Пусть функция f(x) – определена и непрерывна на некотором интервале a < x < b. В таком случае все решения дифференциального уравнения вида y’ = f(x). находятся как Дифференциальное уравнение Такое уравнение можно представить также в виде:
Для решения такого уравнения необходимо: для вида (1)
Для вида (2)
В итоге получится уравнение вида Дифференциальное уравнение называется линейным относительно неизвестной функции и ее производной, если оно может быть записано в виде:
Суть метода заключается в том, что искомая функция представляется в виде произведения двух функций
Потребуем чтобы
Сначала решается уравнение (1) как уравнение с разделяющимися переменными, при его решении константа С=0, затем найденное решение Пример. 1. Решить уравнение Решение:
Ответ: 2. Найти решение дифференциального уравнения Решение:
При у(2) = 1 получаем Итого: Ответ: 3. Решить уравнение Решение: Данное уравнение является линейным неоднородным дифференциальным урвнением первого порядка. Применим метод Бернулли.
Получаем: Ответ: Задания для совместного решения.
Задания для самостоятельного решения.
Занятие 10. Дифференциальные уравнения второго порядка
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-17; просмотров: 92; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.190.167 (0.012 с.) |
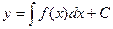 . Если заданы начальные условия х0 и у0, то можно определить постоянную С.
. Если заданы начальные условия х0 и у0, то можно определить постоянную С.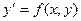 называется уравнением с разделяющимися переменными, если его можно записать в виде
называется уравнением с разделяющимися переменными, если его можно записать в виде 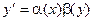 (1).
(1).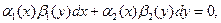 (2)
(2)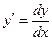 ,
, 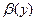 .
.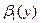
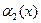 .
.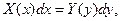 решение которого находится путем интегрирования обеих частей. После нахождения соответствующих интегралов получается общее решение дифференциального уравнения с разделяющимися переменными.
решение которого находится путем интегрирования обеих частей. После нахождения соответствующих интегралов получается общее решение дифференциального уравнения с разделяющимися переменными.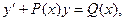 при этом, если правая часть Q(x) равна нулю, то такое уравнение называется линейным однородным дифференциальным уравнением, если правая часть Q(x) не равна нулю, то такое уравнение называется линейным неоднородным дифференциальным уравнением. P(x) и Q(x)- функции непрерывные на некотором промежутке a < x < b. Для решения неоднородного линейного дифференциального уравнения может быть применен метод Бернулли. (Якоб Бернулли (1654-1705) – швейцарский математик.)
при этом, если правая часть Q(x) равна нулю, то такое уравнение называется линейным однородным дифференциальным уравнением, если правая часть Q(x) не равна нулю, то такое уравнение называется линейным неоднородным дифференциальным уравнением. P(x) и Q(x)- функции непрерывные на некотором промежутке a < x < b. Для решения неоднородного линейного дифференциального уравнения может быть применен метод Бернулли. (Якоб Бернулли (1654-1705) – швейцарский математик.)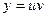 . При этом очевидно, что
. При этом очевидно, что 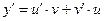 . Подставляя в исходное уравнение, получаем:
. Подставляя в исходное уравнение, получаем: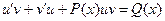
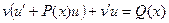
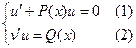
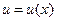 подставляется в уравнение (2) и находится его решение
подставляется в уравнение (2) и находится его решение 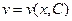 . В итоге находится значение искомой функции
. В итоге находится значение искомой функции 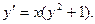
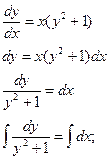
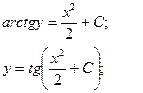
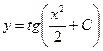
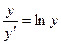 при условии у(2) = 1.
при условии у(2) = 1.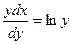
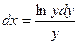
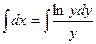
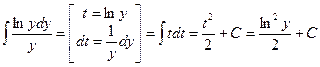
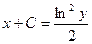 .
.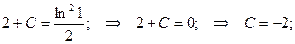
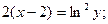 или
или 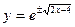 - частное решение;
- частное решение;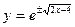
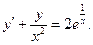
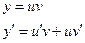 . Подставим в данное уравнение:
. Подставим в данное уравнение:
 (1) (2)
(1) (2) 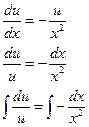
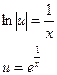
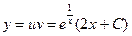 - общее решение.
- общее решение.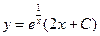
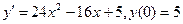
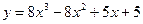
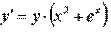
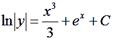 или
или 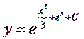
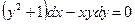
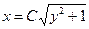
 ,
,