Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Площадь треугольника и четырехугольника ⇐ ПредыдущаяСтр 4 из 4
Подобие треугольников и равенство треугольников
Однако нельзя сказать, что данное отношение является коэффициентом подобия, так как оно может являться комплексным числом, очевидно, отношение сторон двух треугольников комплексным числом не является. Это некий комплексный коэффициент подобия, который указывает отношение только применимо к комплексному методу решения задач. Однако его модуль является коэффициентом подобия. Это приводит к некоторым сложностям, поскольку, зная только коэффициент подобия, мы не можем узнать это комплексное число. Но в большинстве случаев это не помешает решению. Если треугольники на комплексной плоскости противоположно ориентированы, то можно избежать переобозначений и движений одного из треугольников. Для этого достаточно видоизменить формулу таким образом:
Равенство треугольников можно рассматривать как частный случай подобия треугольников, когда комплексное число соответствующее коэффициенту подобия равно 1: то есть необходимо выполнение условия c1 – a1 = c – a, b1 – a1 = b – a, c1 – b1 = c – b (в заданных обозначениях).
Правильные многоугольники
На рис. 4 изображен правильный пятиугольник, вершинами которого являются корни пятой степени из единицы. Для построения многоугольника необходимо найти все комплексные корни.
Рис. 4 При решении задач с правильными многоугольниками бывает удобно поместить центр многоугольника в начало координат, одну из его вершин в точку (1;0).
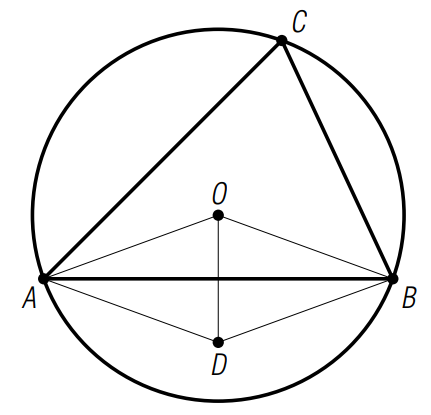
Примеры решения задач Задача 4.1 Точка D симметрична центру описанной около треугольника АВС окружности, относительно АВ. Доказать, что CD = R2 + AC2 + BC2 – AB2. Решение: примем точку О за точку начала координат, тогда уравнение этой окружности: z×z=R2. AOBD – ромб, так как расстояния от О до АВ и от D до АВ равны, OD перпендикулярен АВ. Но тогда OA + OB = OD, а через комплексные координаты а+b=d. Тогда получаем, что:
Рис. 5
Получается, что левая и правая части равны одному и тому же, следовательно, они равны между собой. Что и требовалось доказать. Задача 4.2 На гипотенузе АВ прямоугольного треугольника АВС построен квадрат вне треугольника, найти расстояние от вершины С до центра квадрата, если ВС и АС соответственно равны а и b. Решение: для начала вспомним о геометрическом смысле произведения комплексных чисел. То есть, если мы b умножим на а, то получим поворот b на arg a. Получается, что а выступает в роли параметра, тогда если угол поворота равен 900, т.к. такой угол соответствует чисто мнимому числу, то а=i.
Пусть С является точкой начала координат, СА и СВ действительная и мнимая соответственно, т. е. А(b) и B(ai). Заметим, что BQ при повороте на 900 переходит в QA. Тогда, воспользовавшись ранее рассмотренным случаем, заключаем, что (ai –q)i=b – q, выделяем q и получаем:
Задача 4.3
Дан произвольный четырехугольник, не являющийся трапецией. Прямая соединяет середины противоположных сторон четырехугольника и образует с двумя другими его сторонами равные углы. Доказать, что эти прямые, составляющие равный угол с данной прямой, равны между собой.
Но по условию четырехугольник не трапеция, следовательно, AB не параллельно CD, следовательно, вторая скобка не может обратиться в 0. Тогда первая скобка обращается в 0, но отсюда следует, что AB=CD, ч.т.д.
Задача 4.4
Решение: Возьмем за точку M начало координат. Тогда m=0. Следовательно a0 = a1 – a, b0 = b1 – b, c0 = c1 – c. Отсюда получаем, что b0 – a0 = b1 – a1 – (b – a), c0 – a0 = c1 – a1 – (c – a).
Разделим на b – a и c – a соответственно:
Но по условию выражения в правых частях выражений равны, из чего следует, что:
Это означает подобие первого и третьего треугольников, очевидно, что в таком случае все эти треугольники подобны между собой.
|
||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 139; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.82.79 (0.013 с.) |
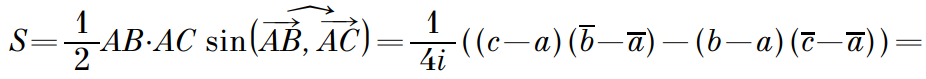 Для нахождения площади треугольника воспользуемся формулой полу произведения смежных сторон треугольника на синус угла между ними. В таком случае возьмем некоторый ΔАВС; АВ=|b – a|, AC=|c – a| и получаем:
Для нахождения площади треугольника воспользуемся формулой полу произведения смежных сторон треугольника на синус угла между ними. В таком случае возьмем некоторый ΔАВС; АВ=|b – a|, AC=|c – a| и получаем: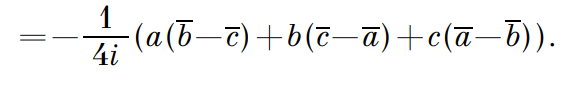
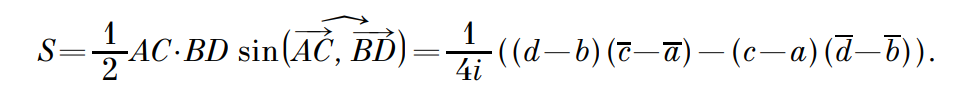 Теперь для нахождения площади четырехугольника воспользуемся формулой, в которой нам также понадобится синус угла – полу произведение диагоналей четырехугольника на синус угла между ними. Возьмем четырехугольник ABCD, в котором точки A, B, C, D имеют соответствующие координаты a, b, c, d. Длины диагоналей – AB=|b – a|, CD=|d – c|. Получаем:
Теперь для нахождения площади четырехугольника воспользуемся формулой, в которой нам также понадобится синус угла – полу произведение диагоналей четырехугольника на синус угла между ними. Возьмем четырехугольник ABCD, в котором точки A, B, C, D имеют соответствующие координаты a, b, c, d. Длины диагоналей – AB=|b – a|, CD=|d – c|. Получаем: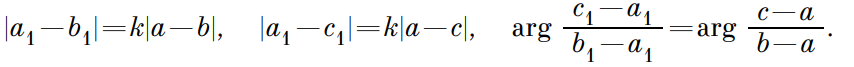 Рассмотрим критерии подобия первого признака подобия треугольников. Пусть имеем некоторые ΔABC и ΔA1B1C1, они являются подобными тогда и только тогда, когда A1B1=k×AB, A1 C1=k×AC и ےBAC=ےB1A1C1. Преобразуем данные равенства, используя алгебру комплексных чисел, если точки А, В, С, А1, В1, С1 имеют соответственные координаты a, b, c, a1, b1, c1:
Рассмотрим критерии подобия первого признака подобия треугольников. Пусть имеем некоторые ΔABC и ΔA1B1C1, они являются подобными тогда и только тогда, когда A1B1=k×AB, A1 C1=k×AC и ےBAC=ےB1A1C1. Преобразуем данные равенства, используя алгебру комплексных чисел, если точки А, В, С, А1, В1, С1 имеют соответственные координаты a, b, c, a1, b1, c1: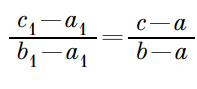 Приводим к единому тождеству:
Приводим к единому тождеству:
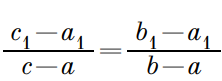 В итоге получаем постоянное отношение, выраженное комплексным числом:
В итоге получаем постоянное отношение, выраженное комплексным числом: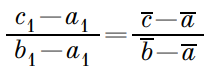
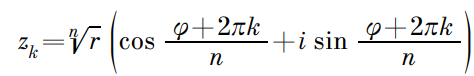 Данный аспект частично рассматривается в курсе алгебры за 10-11 класс. Построение правильного многоугольника тесно связано с нахождением корня n-ой степени из комплексного числа. Поскольку данная тема затрагивается в процессе изучения школьного курса, то не будем выводить формулу для нахождения корней из числа. Эта формула выглядит так:
Данный аспект частично рассматривается в курсе алгебры за 10-11 класс. Построение правильного многоугольника тесно связано с нахождением корня n-ой степени из комплексного числа. Поскольку данная тема затрагивается в процессе изучения школьного курса, то не будем выводить формулу для нахождения корней из числа. Эта формула выглядит так: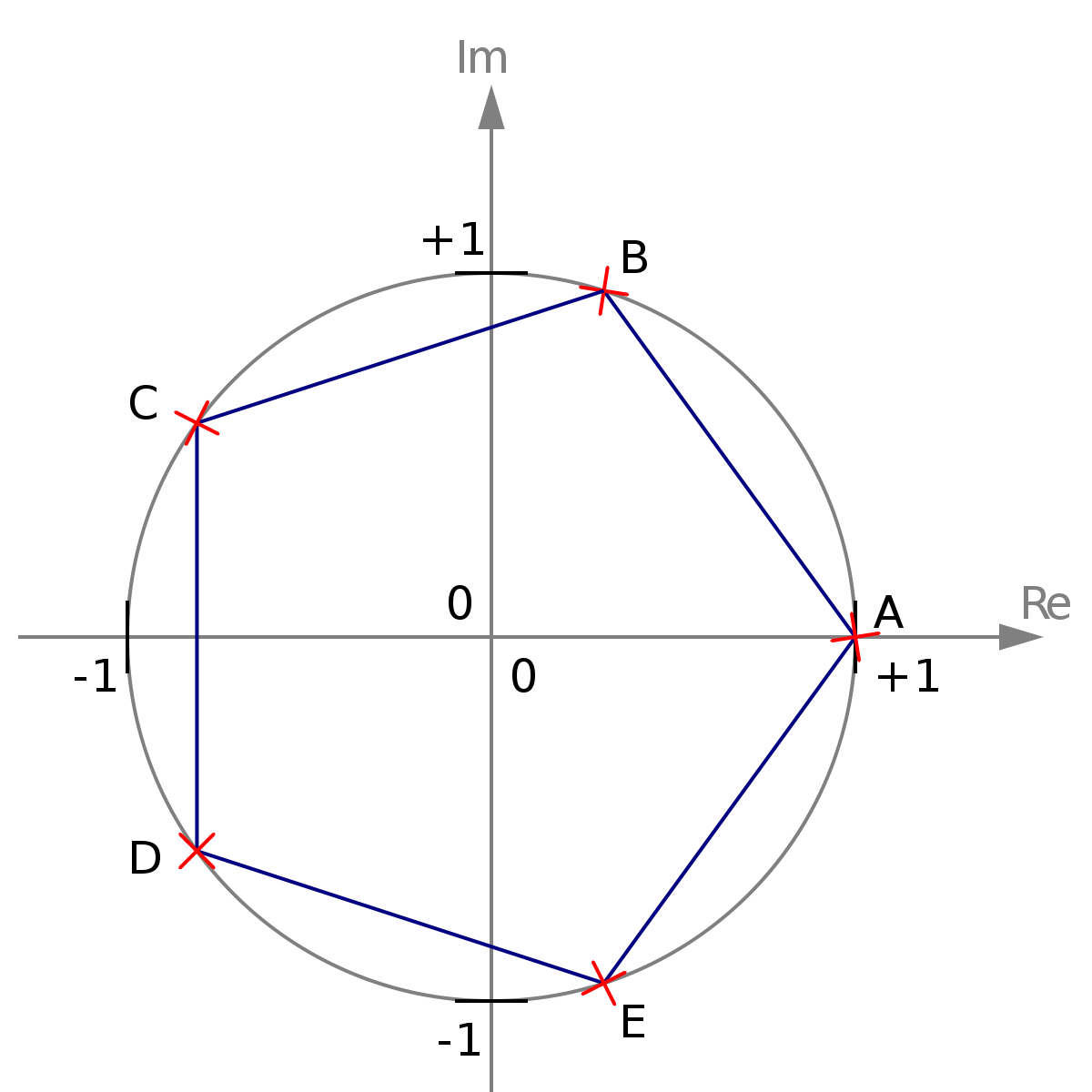
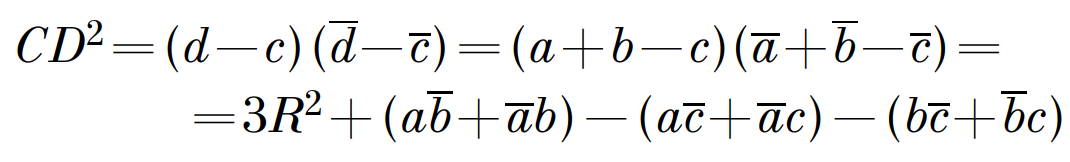
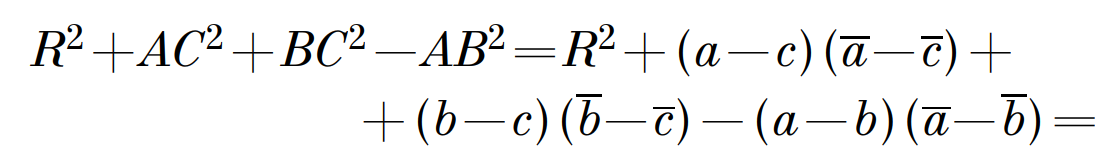 Но:
Но: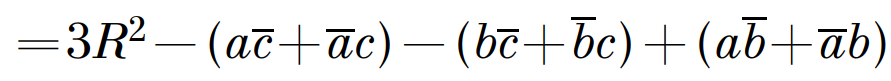
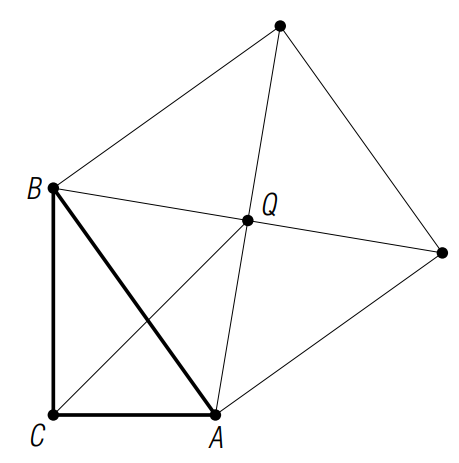
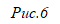 Теперь совершив основные приготовления, приступим к решению самой задачи.
Теперь совершив основные приготовления, приступим к решению самой задачи.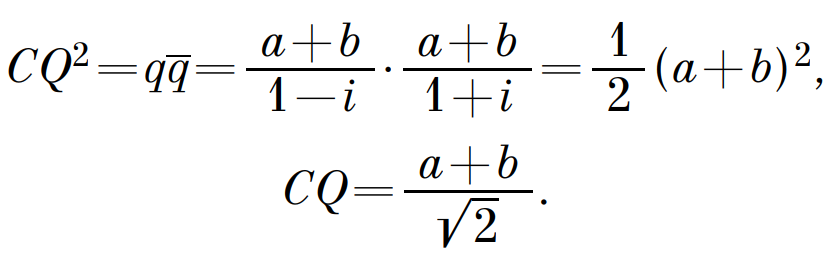
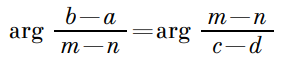
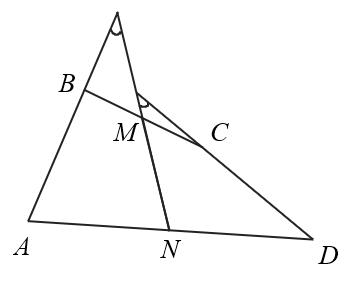 Решение: N и M – середины AD и BC. Углы между AB и MN и между CD и MN равны. Переходим к векторным величинам и выражаем их через комплексные координаты. Выражаем углы, используя алгебру комплексных чисел, так как эти углы равны по условию, то получаем:
Решение: N и M – середины AD и BC. Углы между AB и MN и между CD и MN равны. Переходим к векторным величинам и выражаем их через комплексные координаты. Выражаем углы, используя алгебру комплексных чисел, так как эти углы равны по условию, то получаем: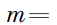
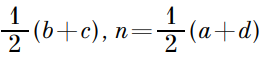 Переносим в левую часть и приравниваем к нулю. Из того, что аргумент равен 0, следует, что данное число является действительным. M и N делят противоположные стороны четырехугольника пополам, в методе комплексных чисел это значит, что:
Переносим в левую часть и приравниваем к нулю. Из того, что аргумент равен 0, следует, что данное число является действительным. M и N делят противоположные стороны четырехугольника пополам, в методе комплексных чисел это значит, что: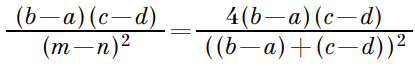 То есть:
То есть: 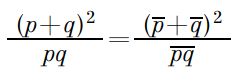
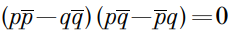 Для удобства обозначим b – a = p, c – d = q, тогда подставляя в полученное выражение, исходя из критерия принадлежности числа к множеству действительных чисел и используя свойства комплексно сопряженных чисел, имеем:
Для удобства обозначим b – a = p, c – d = q, тогда подставляя в полученное выражение, исходя из критерия принадлежности числа к множеству действительных чисел и используя свойства комплексно сопряженных чисел, имеем: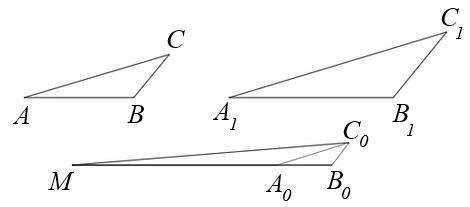 Два треугольника ΔABC и ΔA1B1C1 подобны. МА0, МВ0, МС0 соответственно равны АА1, ВВ1, СС1, причем точка М – произвольная. Доказать, что ΔА0В0С0 подобен данным.
Два треугольника ΔABC и ΔA1B1C1 подобны. МА0, МВ0, МС0 соответственно равны АА1, ВВ1, СС1, причем точка М – произвольная. Доказать, что ΔА0В0С0 подобен данным.