Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модуль комплексного числа и тригонометрическая формула
Модулем комплексного числа, также как и действительного является расстояние от нуля до координаты соответствующей этому числу. Только, если для действительных чисел это отрезок числовой прямой, то для комплексных чисел этим расстоянием служит радиус-вектор. На рис. 1 изображен радиус-вектор ОМ, длина которого равна r. Эта длина и является модулем числа z. Тогда по теореме Пифагора находим, что:
Так как треугольник ОМХ (ОМУ) прямоугольный, то для него справедливы тригонометрические соотношения. Отсюда получаем, что х = r × cosφ, y = r × sinφ. В таком случае число z принимает вид: z = r × (cosφ + i × sinφ). Комплексно сопряженные числа Комплексно сопряженными называются числа, коэффициенты при мнимых частях отличаются знаком. Комплексные координаты таких точек в плоскости комплексных чисел симметричны относительно действительной оси. Число равно своему сопряженному тогда и только тогда, когда коэффициент при мнимой части равен 0, но в таком случае это число является действительным. Тогда условие z=z является критерием принадлежности числа к действительным. Аналогично, если z =-z, то число принадлежит к чисто мнимым.
(Справедливо для всех комплексных чисел) Основы метода комплексных чисел Векторная интерпретация комплексных чисел и действия над ними В этом подразделе мы подробнее разберем взаимосвязь между векторами и комплексными числами (вернее их координатами). Непосредственно на этом и основывается наш способ решения задач. Каждой комплексной координате однозначно соответствует радиус-вектор – модуль конкретного числа. Сложению и вычитанию комплексных чисел в алгебраической форме однозначно отвечает сложение и вычитание соответствующих векторов. То есть, пусть a, b, c – комплексные координаты точек A, B и C, и если выполняется равенство c = a+b, то также выполняется векторное равенство ОС = ОА + ОВ, если допустим с = a – b, то аналогично ОС = ОА – ОВ.
Геометрически это означает, что тоска С является образом точки А в композиции поворота с центром в точке О на угол равный arg b и гомотетии с тем же центром с коэффициентом k = |b|.
Рис. 2
|
||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 128; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.8.82 (0.004 с.) |
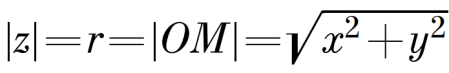 .
.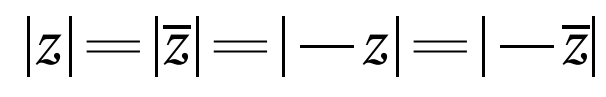 Комплексно сопряженные числа обладают некоторыми полезными свойствами:
Комплексно сопряженные числа обладают некоторыми полезными свойствами: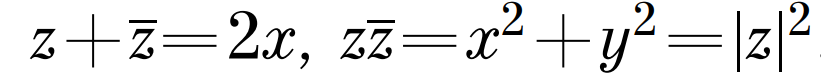
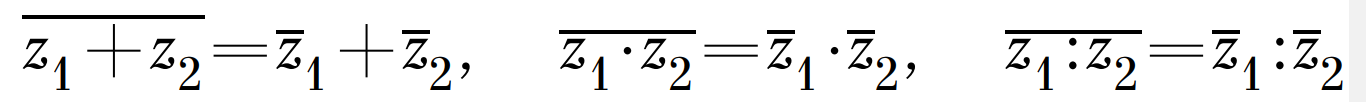
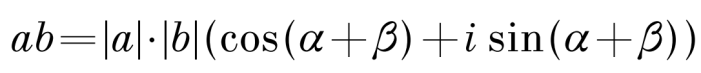 Теперь стоит поговорить о геометрическом смысле умножения комплексных чисел. На рисунке 2 изображены точки А, В и С с комплексными координатами а, b и ab соответственно. Представим числа а и b в тригонометрической форме. Тогда их произведение примет вид:
Теперь стоит поговорить о геометрическом смысле умножения комплексных чисел. На рисунке 2 изображены точки А, В и С с комплексными координатами а, b и ab соответственно. Представим числа а и b в тригонометрической форме. Тогда их произведение примет вид: