
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрический, механический смысл производной.
Введем понятие касательной к графику функции в данной точке. Определение 4. Касательной к графику функции Пусть точка M на кривой соответствует значению аргумента x=0, а точка N и значению аргумента (Рис. 1). Из определения касательной следует, что для ее существования в точке x0 необходимо, чтобы существовал предел Из треугольника MNA видно, что
Если производная функции в точке существует, то, согласно определению производной, получаем
Рис. 1.
Отсюда понятно, что производная Уравнение касательной к кривой 3. Пусть вдоль некоторой прямой движется точка по закону, Тогда предел В определенном смысле производную функции
Дифференцируемость функции. Установим связь между дифференцируемостью и непрерывностью функции в точке. Прежде всего, отметим, что не любая непрерывная функция дифференцирована. Чтобы в этом убедиться, достаточно рассмотреть, например, функцию Теорема 1. Если существует конечная производная функции Доказательство. По условию теоремы, существует производная а по определению предела это означает, что где
Непрерывность функции необходимое, но не достаточное условие дифференцируемости функции. Производная непрерывной функции не обязательно непрерывна. Если функция имеет непрерывную производную на некотором интервале (a,b), то функция называется гладкой на этом промежутке. Если производная функции имеет конечное число точек разрыва первого рода, то такая функция называется кусочно-гладкой на данном интервале. На рис. 2 приведена графическая иллюстрация некоторых возможных значений производной функции в точке x=0.
|
|||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 118; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.223.123 (0.007 с.) |
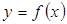 в точке M называется предельное положение секущей MN, когда точка N стремится к точке M по кривой.
в точке M называется предельное положение секущей MN, когда точка N стремится к точке M по кривой.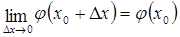 равный углу наклона касательной к оси Ox.
равный углу наклона касательной к оси Ox.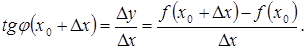

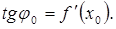
 равна угловому коэффициенту (тангенсу
равна угловому коэффициенту (тангенсу 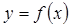 угла наклона к положительному направлению оси Ox касательной к графику функции в точке
угла наклона к положительному направлению оси Ox касательной к графику функции в точке  ). В этом состоит геометрический смысл производной.
). В этом состоит геометрический смысл производной.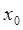 имеет вид
имеет вид 
 где s икс пройден путь, t икс время. Необходимо найти скорость точки в момент t0. К моменту t0 пройденный путь равен
где s икс пройден путь, t икс время. Необходимо найти скорость точки в момент t0. К моменту t0 пройденный путь равен  , а к моменту
, а к моменту 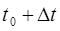 вклада путь
вклада путь  . Средняя скорость
. Средняя скорость 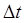 за время равна
за время равна 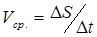 .
.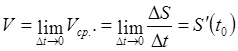 определяет мгновенную скорость точки в момент времени t=0, как производную пути по времени.
определяет мгновенную скорость точки в момент времени t=0, как производную пути по времени.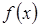 и быстрее растет функция. В этом состоит механический смысл производной.
и быстрее растет функция. В этом состоит механический смысл производной.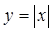 . В точке эта функция непрерывна, но не является дифференцированной (не существует производной, потому что не существует касательной).
. В точке эта функция непрерывна, но не является дифференцированной (не существует производной, потому что не существует касательной).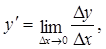

 a бесконечно мала функция
a бесконечно мала функция 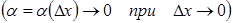 . Тогда,, где
. Тогда,, где  , де
, де 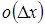 бесконечно имела величина более высокого порядка малости по сравнению с.
бесконечно имела величина более высокого порядка малости по сравнению с.  Из последнего равенства получается, что,
Из последнего равенства получается, что,  а это значит, что
а это значит, что 


