
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема. Производная, ее геометрический и физический смысл. Правило дифференцирования функций. Дифференцирование функций, заданных аналитически.Стр 1 из 3Следующая ⇒
Лекция (занятия №24-25) Тема. Производная, ее геометрический и физический смысл. Правило дифференцирования функций. Дифференцирование функций, заданных аналитически.
План. 1. Определение производной функции. 2. Геометрический, механический смысл производной. 3. Дифференцируемость функции. 4. Схема вычисления производной. 5. Основные правила дифференцировки. 6. Производная сложной и обратной функций. 7. Производные элементарных функций.
Определение производной. Производная играет чрезвычайно важную роль в математическом анализе, являясь основным понятием дифференциального исчисления. Рассмотрим функцию Определение 1. Если существует предел отношения приращения функции
Производная функции имеет несколько обозначений Рассматривая все значения x з (a,b), в которых Нахождение производной функции называется дифференцированием этой функции. Если функция в точке x имеет конечную производную, то функция называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках интервала (a,b), называется дифференцированной на этом интервале. Определение 2. Функция Определение 3. Правой производной функции Левой производной функции Для того чтобы существовала производная
Дифференцируемость функции. Установим связь между дифференцируемостью и непрерывностью функции в точке. Прежде всего, отметим, что не любая непрерывная функция дифференцирована. Чтобы в этом убедиться, достаточно рассмотреть, например, функцию Теорема 1. Если существует конечная производная функции Доказательство. По условию теоремы, существует производная а по определению предела это означает, что где Непрерывность функции необходимое, но не достаточное условие дифференцируемости функции. Производная непрерывной функции не обязательно непрерывна. Если функция имеет непрерывную производную на некотором интервале (a,b), то функция называется гладкой на этом промежутке. Если производная функции имеет конечное число точек разрыва первого рода, то такая функция называется кусочно-гладкой на данном интервале. На рис. 2 приведена графическая иллюстрация некоторых возможных значений производной функции в точке x=0.
КОНТРОЛЬНЫЕ ВОПРОСЫ. 1. Сформулируйте определение производной. 2. Какой геометрический, механический и экономический смысл производной? 3. Что можно сказать о поведении функции, зная, что ее производная положительна? Отрицательная? Недодатна? Неотъемлемая? Сделайте рисунки для этих случаев, приведите примеры таких функций. 4. Дайте определение левой и правой производной. 5. Связь между существованием производной и непрерывностью функции? 6. Может ли функция иметь производную в точке, в которой она разрывная? 7. Функция в данной точке дифференцирована. Значит ли это, что она непрерывна в этой точке?
8. Почему равны производные суммы, разницы и произведения двух функций? 9. Выпишите вид производной доли двух функций. 10. Чему равна производная сложной функции? Выпишите формулу и приведите примеры. 11. Напишите формулы дифференцирования основных элементарных функций. 12. Как определяются производные высших порядков? ОСНОВНЫЕ ТЕРМИНЫ И ПОНЯТИЯ. Производная функции. Дифференцирование функции. Производные высших порядков. Касательная. Геометрический смысл производной Уравнение касательной к кривой Механический смысл производной Кусочно-гладкая функция.
ЛИТЕРАТУРА. 1. М. С. Красс " Математика для экономических специальностей: Учебник”, М.: ИНФРА-М, 1999, с. 81-85, 87-94, 95-97. 2. “ Высшая математика для экономистов”, ред. Н. Ш. Кремера Н.: ЮНИТИ, 1998, с. 176-208. 3. В.В. Пак, Ю.Л. Носенко “Высшая математика” Д.: Сталкер, 1997, с. 111-124. 4.В. А. Курявцев, В. П. Демидович “Короткий курс высшей математики", г. Наука, 1975, гл. IX, X. 5. “Курс математики для техникумов, ч. 1”, ред. Н.М. Матвеева, М.: Наука, 1976, с. 103-116. 6. Ю. М. Почтман Основы математики: учебно-методическое пособие”, М.: МАУП, 1999, с. 39-44. 7. И. Л. Зайцев " элементы высшей математики (для техникумов)", М.: Наука, 1974, гл. 3. Лекция (занятия №24-25) Тема. Производная, ее геометрический и физический смысл. Правило дифференцирования функций. Дифференцирование функций, заданных аналитически.
План. 1. Определение производной функции. 2. Геометрический, механический смысл производной. 3. Дифференцируемость функции. 4. Схема вычисления производной. 5. Основные правила дифференцировки. 6. Производная сложной и обратной функций. 7. Производные элементарных функций.
Определение производной. Производная играет чрезвычайно важную роль в математическом анализе, являясь основным понятием дифференциального исчисления. Рассмотрим функцию Определение 1. Если существует предел отношения приращения функции
Производная функции имеет несколько обозначений Рассматривая все значения x з (a,b), в которых Нахождение производной функции называется дифференцированием этой функции. Если функция в точке x имеет конечную производную, то функция называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках интервала (a,b), называется дифференцированной на этом интервале. Определение 2. Функция Определение 3. Правой производной функции
Левой производной функции Для того чтобы существовала производная
|
|||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 277; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.147.215 (0.019 с.) |
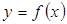 , заданную на некотором интервале (a,b). Возьмем произвольную точку
, заданную на некотором интервале (a,b). Возьмем произвольную точку 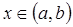 и зададим в этой точке прирост
и зададим в этой точке прирост  такой, что
такой, что 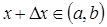 . При этом функция получит приращение
. При этом функция получит приращение 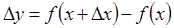 .
.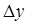 к приращению аргумента
к приращению аргумента 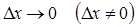 , то этот предел называется производной функции
, то этот предел называется производной функции 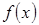 в точке
в точке 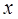
 (1)
(1) Иногда в обозначении производной используется индекс, указывающий, по какой переменной взята производная, например
Иногда в обозначении производной используется индекс, указывающий, по какой переменной взята производная, например  .
.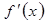 существует, мы видим, что каждой точке x соответствует определенное значение
существует, мы видим, что каждой точке x соответствует определенное значение 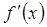 . Итак,
. Итак, 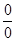 .
. или
или  , если в этой точке граница (1) бесконечная:
, если в этой точке граница (1) бесконечная: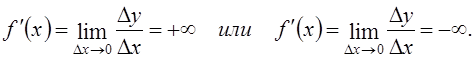 (1)
(1) (2)
(2)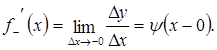 (3)
(3)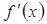 , необходимо и достаточно, чтобы существовали производные от f в точке x справа и слева и были равны между собой. Тогда автоматически они равны.
, необходимо и достаточно, чтобы существовали производные от f в точке x справа и слева и были равны между собой. Тогда автоматически они равны. 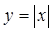 . В точке эта функция непрерывна, но не является дифференцированной (не существует производной, потому что не существует касательной).
. В точке эта функция непрерывна, но не является дифференцированной (не существует производной, потому что не существует касательной).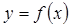 в точке x, то f(x) непрерывная в этой точке.
в точке x, то f(x) непрерывная в этой точке.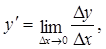

 a бесконечно мала функция
a бесконечно мала функция 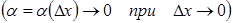 . Тогда,, где
. Тогда,, где  , де
, де 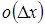 бесконечно имела величина более высокого порядка малости по сравнению с.
бесконечно имела величина более высокого порядка малости по сравнению с.  а это значит, что
а это значит, что 


