
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определители 2-ого и 3-ого порядка и их св-ва.Стр 1 из 4Следующая ⇒
Линейные операции над матрицами; их свойства. Сложение матриц Пусть А=(аij)и B=(bij) — матрицы одинаковых размеров
Нельзя:
Умножение матрицы на число Произведением матрицы А=(а ij) на число
Вычитание А-В = В + (-1)В = С Найти 2A-B, если
Свойства линейных операций над матрицами: 1. А+В = В+А - коммутативность 2. (А+В) + С = А + (В+С) – ассоциативность 3. Нулевая матрица О. А+О=А 4. (α+β)*А = αА +βА 5. α*(А+В) = αА + αВ 6. Е*А = А 7. α(βА) = αβА Произведение матриц, его свойства. Правило умножения матриц а на матрицу b определяется, только для того случая, когда число столбцов матрицы а = числу строк матрицы b m*n A = (aij) n*q B = (bjk) => A*B = C C=(cik) m*q cik = ∑nj=1aijbjk A = (a11, a12, a13) *B = (b11 = C=AB = a11 b11 + a12 b12 + a13 b13 b12 b13) В общем случае, как следует из определения элемент cik – есть сумма произведений элементов i- строки на элементы k – столбца.
Произведение двух матриц в общем случае зависит от порядка сомножителей, т.е не является коммутативным: АВ ≠ ВА, если АВ=ВА, то матрицы коммутативны. А = (а11 а12) – табл; det А = | а11 а12| = с (321)*(3 8 9 = ВА=С(1*3) - можно(наоборот нельзя) 2 4 5 7 1 2) У квадратной матрицы одного порядка произв АВ и ВА – всегда сущ-ет Квадратная матрица А наз-ся не вырожденной или неособенной, если ее деторминант отличен от 0 detA ≠ 0 detA = 0 А= (а11 а12 det A = |а11 а12| = c (число) а21 а22) - табл |a21 а22|
det A = 0 – выражденная (необратная) det A ≠ 0 – можно обрат найти – неособенная А-1 – наз-ся обратной квадратной матрицы А, если выполн сл условия: А-1А = АА-1 = Е (1) Тh – Всякая неособенная матрица А имеет обратную
Система линейных уравнений. Формулы Крамера. Способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Если число уравнений системы (3.1) равно числу неизвестных, т.е. Теорема 1. Если определитель
Пример:
Определители:
Уравнение прямой с угловым коэффициентом; уравнение прямой через одну и две точки Пересечение прямой с плоскостью. Условие принадлежности прямой плоскости. Определение угла между векторами. Условие параллельности и перпендикулярности векторов. Определители 2-ого и 3-ого порядка и их св-ва. Определитель – это число, записанное в виде таблицы. аij: i- строка, j-столб Опред 2-ого порядка – это чило вяч-ое по сл формуле: Опред 3-ого порядка – это число выч сл образом: (показ три способа) Св-ва: 1. Величина определителя не изменится, если все его строки заменить столбцами, причем каждую строку заменить столбцом с тем же номером, то есть
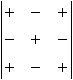
2. Перестановка двух столбцов или двух строк определителя равносильна умножению его на -1.
3. Если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.
4. Умножение всех элементов одного столбца или одной строки определителя на любое число k равносильно умножению определителя на это число k. Например,
5. Если все элементы некоторого столбца или некоторой строки равны нулю, то сам определитель равен 0. 6. Если соответствующие элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю.
7. Если каждый элемент n-го столбца или n-й строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце или соответственно в n-й строке имеет первые из упомянутых слагаемых, а другой - вторые; элементы, стоящие на остальных местах, у вех трех определителей одни и те же. Например,
8. Если к элементам некоторого столбца (или некоторой строки) прибавить соответствующие элементы другого столбца (или другой строки), умноженные на любой общий множитель, то величина определителя при этом не изменится. Например,
9. Минором некоторого элемента называется определитель, получаемый из данного путем вычеркиванием строки и столбца, на пересечении которых расположен этот элемент, этот определитель будет на порядок ниже основного. aij->Mij Aij=Mij(-1)i+j Алгебраическое дополнение элемента определителя – это Mij данного элемента * на (-1)i+j Aij=Mij(-1)i+j
Th: опре-ль равен сумме произведений элементов какого-либо столбца (или строки) на их алгебраические дополнения.
2 Понятие определителя n-ого порядка: разложение по строке (столбцу). Привести пример. Теорема о разложении определителя по строке позволяет свести вычисление определителя матрицы n×n к вычичлению n определителей матриц (n-1)×(n-1). Таким образом, вычисление определителей с порядком выше третьего сводится к разложению на сумму определителей третьего порядка. С помощью описанных выше свойств определителей можно провести предварительные преобразования матрицы, облегчающие дальнейшие вычисления. Например, если перед разложением определителя n-го порядка по какой-либо строке накопить в этой строке нули, то разложение приводит к меньшему количеству определителей порядка n-1. Ниже приводится пример, в котором сначала из первой строки вычитается вторая (при этом появляются два нуля), а затем идет разложение по первой строке (из-за двух нулей получается не четыре определителя третьего порядка, а только два): 3 Матрица. Общие определения. Матрица – это таблица чисел. [A]=aij=||aij|| i (m)-строка, (n)j-столб Если матрица сод-ит из n строк и m столбцов, то эта матрица размера m*n или прямоугольная (m=n – квадратная размера n) Классификация матриц: Диагональной - квадратная матрица, у кот все элементы вне главной диагонали = нулю. Скалярная- это произведение скаляра и единичной матрицы. а11=а22=аmn=а [S] Единичной - диагональная матрица с единицами на главной диагонали. Нулевой - матрица, все элементы кот равны нулю. Две матрицы А и В называются равными (А=В), если они одинакового размера (т.е. имеют один кол-во строк и один кол столбцов и их соответств элементы равны).
|
||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 72; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.67.26 (0.023 с.) |
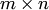 . Матрица C=(cij) тех же размеров
. Матрица C=(cij) тех же размеров 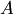 и
и  , если ее элементы равны сумме соответствующих элементов матриц
, если ее элементы равны сумме соответствующих элементов матриц 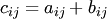
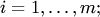
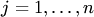 . Сумма матриц обозначается
. Сумма матриц обозначается  . Операция сложения матриц определена только для матриц одинаковых размеров и выполняется поэлементно:
. Операция сложения матриц определена только для матриц одинаковых размеров и выполняется поэлементно: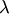 называется матрица C =(cij) тех же размеров, что и матрица А, каждый элемент которой равен произведению числа
называется матрица C =(cij) тех же размеров, что и матрица А, каждый элемент которой равен произведению числа  (
(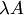 или
или 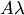 .)
.)
 ,
,  .
.  .
. , то имеет место
, то имеет место матрицы системы (3.1) не равен нулю, то система (3.1) имеет единственное решение, вычисляемое по формулам Крамера
матрицы системы (3.1) не равен нулю, то система (3.1) имеет единственное решение, вычисляемое по формулам Крамера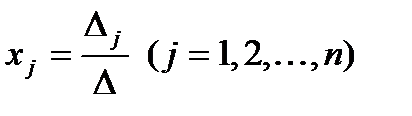 , где
, где 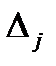 - определитель матрицы, получаемой из матрицы А системы (3.1) заменой j -го столбца столбцом свободных членов.
- определитель матрицы, получаемой из матрицы А системы (3.1) заменой j -го столбца столбцом свободных членов.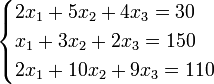

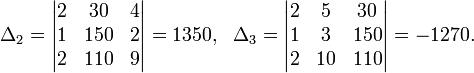
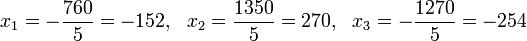

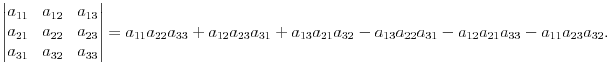
 .
.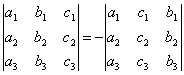 .
.
 .
.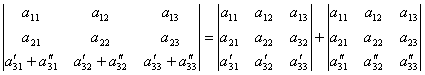

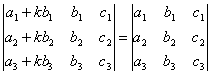 .
.
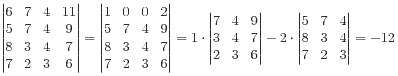


 то А=B, если a11=b11, a12=b12, a21=b21, a22=b22
то А=B, если a11=b11, a12=b12, a21=b21, a22=b22


