
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа. Математическая обработка результатов измерений и представление результатов эксперимента
Классификация погрешностей
Истинное значение физической величины абсолютно точно определить нельзя. При измерениях физических величин под действием самых разнообразных причин возникают погрешности измерений. Все погрешности принято разделять на систематические, случайные и промахи (ошибки). Систематической называют такую погрешность, которая остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины. Такие погрешности появляются вследствие неисправности приборов, неточности метода исследования, каких-либо упущений экспериментатора, а также при использовании для вычислений неточных зависимостей (формул), констант и т.д. Случайной называется погрешность, которая вызывается действием не поддающихся контролю многочисленных, независимых друг от друга факторов. Значение случайной погрешности колеблется от одного измерения к другому, что делает невозможным точное предсказание результата в каждом отдельном измерении. Однако при рассмотрении повторных измерений обнаруживается характерная закономерность результатов, их определенная устойчивость, которая и служит основой для математической обработки опытных данных, вычисления случайных погрешностей. Промахом или ошибкой называют такую погрешность измерения, которая оказывается значительно больше ожидаемой при данных условиях. Ошибка обязательно должна быть исключена из результатов измерений.
Определение погрешностей при прямых измерениях
Прямыми называют такие измерения, при которых физическая величина измеряется непосредственно при помощи прибора. Пусть х – действительное значение измеряемой величины, а х1 – показания прибора. Абсолютной погрешностью называется величина
Точность измерения характеризуется отношением абсолютной погрешности к действительному значению измеряемой величины
Это отношение называется относительной погрешностью и выражается в процентах. Погрешности, допускаемые при прямых измерениях, нередко называются приборными, так как обусловлены классом точности прибора, который указывается либо на самом приборе, либо в паспорте. В тех случаях, когда на приборе класс точности не указан, абсолютная погрешность принимается равной половине цены деления.
Случайные погрешности имеют статистический характер, их математическая обработка производится с помощью теории вероятностей. При многократном измерении равновероятно получить результат как больший, так и меньший, чем истинное значение измеряемой величины. Пусть проведено n измерений величины х и в результате получено n значений: х1, х2, …хn. Величина
называется средним арифметическим значением, является хорошим приближением к истинному значению измеряемой величины и, как правило, используется как окончательный итог серии измерений. Рассмотрим несколько основных этапов упрощенной математической обработки результатов измерений. 1. Находим среднее арифметическое значение измеряемой величины 2. Вычисляем абсолютные погрешности результатов отдельных измерений
Абсолютная погрешность имеет размерность измеряемой величины и характеризует качество отдельных измерений. 3. Вычисляем среднюю абсолютную погрешность
4. Вычисляем относительную погрешность
5. Записываем окончательный результат
Определение погрешностей при косвенных измерениях
В большинстве случаев при проведении физических экспериментов исследуемая физическая величина не может быть измерена непосредственно, для ее определения требуется измерить ряд других величин, а искомую найти, подставив найденные значения в формулу, выражающую зависимость искомой величины от непосредственно измеряемых величин. Такие измерения называют косвенными. Для определения погрешностей косвенных измерений можно воспользоваться формулами дифференцирования, т.к. формулы погрешностей получаются в том же приближении, что и формулы для дифференциала функции. Во многих случаях, когда формула удобна для логарифмирования, оказывается более удобной формула относительной погрешности. Относительная погрешность
Иначе говоря, относительную погрешность можно рассчитать, если взять дифференциал натурального логарифма, определяющий зависимость данной величины от измеряемых величин. Наиболее часто встречающиеся формулы приведены в таблице 1.1.
Таблица 1.1
Правила округления
Точно измерить физическую величину нельзя, поэтому результаты измерений носят приближенный характер. Степень приближенности определяется задачей исследования. Таким образом, все вычисления в физике проводятся с приближенными числами. При округлении какого-либо числа до какого-либо разряда необходимо все числа, стоящие справа от этого разряда, отбросить. Если старшая отбрасываемая цифра меньше 5, то последняя оставляемая цифра не изменяется. Если старшая отбрасываемая цифра больше или равна 5, то последняя сохраняемая цифра увеличивается на единицу. Если же после цифры 5, которую нужно отбросить, нет цифр или стоят только нули, то последняя сохраняемая цифра не изменяется, если она четная, и увеличивается, если она нечетная. Если при округлении последняя округляемая цифра оказалась нулем, то его следует писать, даже если он стоит в разряде десятичных дробей. Из правил округления имеется существенное исключение: при округлении погрешностей последняя сохраняемая цифра увеличивается на единицу, если старшая отбрасываемая цифра 3 или больше 3.
2 Лабораторная работа. ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТЕЙ ГАЗОВ ПО МЕТОДУ КЛЕМАНА И ДЕЗОРМА Цель работы: определение отношения молекулярной теплоемкости воздуха при постоянном давлении СР к молекулярной теплоемкости при постоянном объеме 2.1 Основные понятия и закономерности Теплоемкостью вещества называют физическую величину, равную количеству тепла, необходимого для нагревания вещества, на один градус 1 °С (или на 1 К). где d Q – бесконечно малое количество тепла, полученное веществом, dT – бесконечно малое изменение (приращение) его температуры. Теплоемкость зависит от массы нагреваемого тела. Количество тепла, которое надо сообщить единице массы этого вещества, чтобы повысить его температуру на 1 К (или 1 °С), называют удельной теплоемкостью с: Молярной теплоемкостью С вещества называют физическую величину, численно равную количеству тепла, необходимого для нагревания одного моль вещества на один градус: где Из соотношений (2.2) и (2.3) можно определить количество теплоты, получаемое телом:
и связь удельной с и молярной С теплоемкостей: где m – масса одного моля газа. У твердых и жидких тел величина теплоемкости не зависят от условий их нагревания. Теплоемкость газов зависит от условий нагревания. Это связано с тем, что подводимое к газу тепло расходуется не только на повышение внутренней энергии газа, которое обуславливает повышение его температуры, но и на совершение работы против внешних сил. При нагревании газа при постоянном объеме рассматривается теплоемкость при постоянном объеме С V, при постоянном давлении С P. Чтобы установить различия между теплоемкостями С p и С V и связь между ними, воспользуемся первым началом (законом) термодинамики – всеобщий закон сохранения и превращения энергии, который формулируется так: где U – внутренняя энергия системы, т.е. сумма всех видов кинетической и потенциальной энергии всех составных частей системы: молекул, атомов, электронов и т.д. Для идеального газа внутренняя энергия представляет только кинетическую энергию хаотического теплового движения молекул, работа d А и теплота dQ – две формы передачи энергии от одного тела к другому. Работа газа против сил внешнего давления равна: где P – внешнее давление, dV – приращение объема газа. Рассмотрим применение первого начала термодинамики к изопроцессам для данной массы газа. Изопроцессами называются термодинамические процессы, протекающие при постоянном значении одного из параметров состояния (P, V, T).
Изохорический процесс Изохорический процесс протекает при постоянном объеме V = const, т.е. dV = 0, следовательно, dA = pdV = 0. Первое начало термодинамики имеет вид: Тепло, подводимое к системе, идет на увеличение ее внутренней энергии (нагревание газа) из соотношения (2.2)
где с V – удельная теплоемкость при постоянном объеме – количество тепла, которое идет на нагревание 1 кг газа на 1 К при постоянном объеме. Молярная теплоемкость при постоянном объеме CV – теплоемкость одного моля: отсюда изменение внутренней энергии для любой массы m: Приращение внутренней энергии идеального газа равно: где i – число степеней свободы (число независимых перемещений, определяющих состояние молекул газа), Поэтому Изобарический процесс Изобарический процесс – процесс, протекающий при постоянном давлении Р = const, dP = 0. Первое начало термодинамики для этого процесса запишется так: Тепло, подводимое к системе, идет на увеличение внутренней энергии dU и на совершение газом работы над внешними телами dA = PdV. Из определения молярной теплоемкости (6.3) имеем: где Следовательно, получим Найдем значение Запишем уравнение Клапейрона-Менделеева для одного моля газа Изменение температуры газа при P = const прямо пропорционально изменению объема dV, т.е. где Следовательно, где R – универсальная газовая постоянная. Учитывая соотношения (2.15) и (2.17), имеем: – уравнение Майера устанавливает связь между молярными теплоемкостями СР и СV. Из соотношения (2.17) можно выяснить физический смысл универсальной газовой постоянной – она численно равна работе, совершаемой одним молем газа в результате нагревания на 1 К при постоянном давлении. Учитывая (2.13) и (2.18), получим: При нагревании 1 моля газа на 1 К при изобарическом процессе часть теплоты CV идет на увеличение внутренней энергии, и часть, равная R, – на работу против внешних сил.
Изотермический процесс
Изотермический процесс – процесс, протекающий при постоянной температуре T = const, dT = 0, P × V = const. Изменение внутренней энергии Первое начало термодинамики для этого процесса:
Тепло в этом случае идет только на совершение работы против внешних сил (расширение газа). В термодинамике, кроме изопроцессов, рассматривается адиабатический процесс.
Адиабатический процесс
Адиабатический процесс – процесс, протекающий в условиях полной теплоизоляции, т.е. количество теплоты, получаемое газом равно нулю: Первое начало термодинамики: при адиабатическом процессе работа газа над внешними телами совершается за счет уменьшения внутренней энергии. Если объем газа увеличивается, то его температура уменьшается, так как уменьшается его внутренняя энергия. Для адиабатического процесса имеет место уравнение Пуассона: где Уравнение Получим уравнение адиабатического процесса (уравнение Пуассона) в интегральной форме. Запишем уравнение Клапейрона-Менделеева для одного моля газа: и, дифференцируя это уравнение, имеем: Преобразуем уравнение (2.21) и (2.25), для этого умножим уравнение (2.21) на R, а уравнение (2.25) на CV: Сложим эти уравнения почленно: или Учитывая, что Разделим это уравнение на СV: где И тогда можно записать в форме: Полученное соотношение является так же, как и (2.21) уравнением адиабаты в дифференциальной форме. Делим обе части этого уравнения на P × V: где Величина, стоящая в скобках, является постоянной, так как ее дифференциал равен нулю. Обозначим ее (ln const). Тогда можем записать: или Это соотношение – уравнение адиабаты (Пуассона) (2.22). Используя соотношения (2.13) и (2.19), можно записать значение показателя адиабаты через степени свободы:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 378; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.238.70 (0.071 с.) |
 . (1.1)
. (1.1)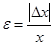 . (1.2)
. (1.2)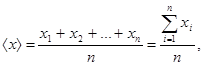 (1.3)
(1.3)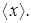
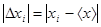
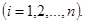 (1.4)
(1.4) (1.5)
(1.5)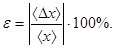 (1.6)
(1.6)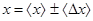 . (1.7)
. (1.7)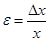 , но
, но 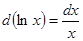 и, следовательно,
и, следовательно, 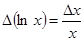 .
.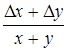

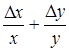
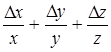



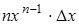




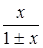
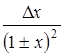



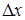
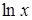

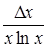
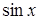


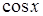
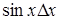
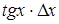



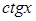

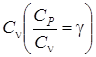 .
. , (2.1)
, (2.1) . (2.2)
. (2.2) , (2.3)
, (2.3)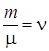 – количество вещества – число молей в данной массе.
– количество вещества – число молей в данной массе. (2.4)
(2.4)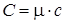 , (2.5)
, (2.5) , (2.6)
, (2.6) , (2.7)
, (2.7)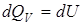 , (2.8)
, (2.8) , (2.9)
, (2.9)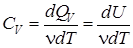 . (2.10)
. (2.10)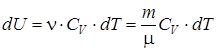 . (2.11)
. (2.11) , (2.12)
, (2.12)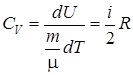 . (2.13)
. (2.13)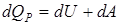 . (2.14)
. (2.14)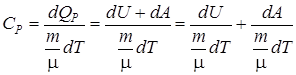 ,
, 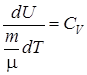 .
.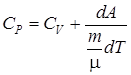 . (2.15)
. (2.15)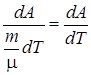 для одного моля.
для одного моля.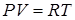 . (2.16)
. (2.16) ,
,  - работа газа.
- работа газа.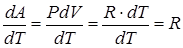 , (2.17)
, (2.17) (2.18)
(2.18)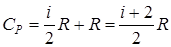 . (2.19)
. (2.19) .
. . (2.20)
. (2.20) , (2.21)
, (2.21) , (2.22)
, (2.22) – показатель адиабаты. (2.23)
– показатель адиабаты. (2.23)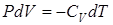 для одного моля – первое начало термодинамики в дифференциальной форме.
для одного моля – первое начало термодинамики в дифференциальной форме.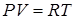 (2.24)
(2.24)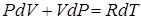 . (2.25)
. (2.25)

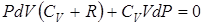 .
. 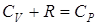 (уравнение Майера), получим:
(уравнение Майера), получим: . (2.26)
. (2.26)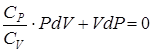 ,
, 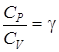 - показатель адиабаты.
- показатель адиабаты.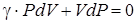 . (2.27)
. (2.27) , (2.28)
, (2.28) ,
, , т.е. дифференциалы натуральных логарифмов V и P, поэтому
, т.е. дифференциалы натуральных логарифмов V и P, поэтому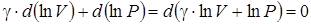 .
.
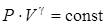 . (2.29)
. (2.29) . (2.30)
. (2.30)


