
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отдельные задачи теплопроводности при стационарном
Режиме В технике часто возникают задачи определения температурного поля тела и установления законов передачи теплоты. В результате решения дифференциального уравнения теплопроводности совместно с условиями однозначности можно найти температурное поле, а на основании закона Фурье ¾ соответствующие тепловые потоки. Следует отметить, что аналитическое решение поставленной задачи возможно только для тел правильной геометрической формы и при достаточно простых условиях однозначности. В остальных случаях эта задача решается численными или экспериментальными методами. Рассмотрим несколько тел простой формы — таких, как плоская стенка и полая труба — в случае стационарного распространения теплоты, для которых уравнение теплопроводности значительно упрощается. 4.2.7.1. Теплопроводность через плоскую и цилиндрическую стенки. Рассмотрим однородную плоскую однослойную стенку толщиной d, (рис. 4.4), имеющую неограниченную длину и ширину. На наружных поверхностях стенки поддерживаются постоянные температуры t1 и t2. Коэффициент теплопроводности стенки постоянен и равен l. При стационарном режиме ¶t/¶t=0 и отсутствии внутренних источников теплоты qv=0 и с учетом того, что в этом случае температура будет изменяться только в направлении оси ОХ, дифференциальное уравнение теплопроводности примет вид
Интегрируя уравнение (4.22), находим
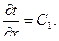 (4.23) (4.23)
Рис. 4.4. Температурное поле плоской однослойной стенки После второго интегрирования получаем общий вид уравнения распределения температур в плоских стенках: t=C1x+C2. (4.24) Постоянные С1 и С2 в уравнении (2.24) определяются из граничных условий: при х=0 t=t1, C 2= t 1; при х=d t=t2, Подставляя значения постоянных С1 и С2 в уравнение (4.24), получаем уравнение распределения температуры в рассматриваемой плоской однослойной стенке
Уравнение (4.25) является уравнением прямой линии. Плотность теплового потока, проходящего через стенку в соот-ветствии с законом Фурье, q = -l¶t/¶n. Учитывая, что
Отношение d/l (Вт/(м2×К)) называется тепловой проводимостью стенки, а обратная величина d/l (м2×К/Вт) — тепловым или термическим сопротивлением стенки. Последнее представляет собой изменение температуры в стенке на единицу плотности теплового потока. Тепловой поток, который передается через полную поверхность стенки,
Для многослойных стенок уравнение имеет вид
Величина При сравнении переноса теплоты через многослойную стенку и стенку из однородного материала удобно ввести в рассмотрение эквивалентный коэффициент теплопроводности lэкв многослойной стенки. Он равен коэффициенту теплопроводности однородной стенки, толщина которой D равна толщине многослойной стенки
Отсюда
Из уравнения (4.29) следует, что эквивалентный коэффициент теплопроводности lэкв зависит не только от теплофизических свойств слоев, но и от их толщины. Графически распределение температур по сечению многослойной стенки представляется ломаной линией; температуры на границе соприкосновения слоев можно определить уравнением
При рассмотрении стационарного процесса теплопроводности в цилиндрической однослойной стенке (трубе) с внутренним радиусом r1 и наружным r2 (рис. 4.5) получаем уравнение распределения температуры:
или
Рис. 4.5. Температурное поле однослойной цилиндрической стенки Уравнение (4.31) представляет собой уравнение логарифмической кривой. То обстоятельство, что распределение температуры в цилиндрической стенке является криволинейным, можно объяснить следующим. В случае плоской стенки плотность теплового потока остается одинаковой для всех изотермических поверхностей и градиент температуры сохраняет для всех изотермических поверхностей постоянную величину. В случае цилиндрической стенки плотность теплового потока через любую изотермическую поверхность изменяется, т. к. величина поверхности зависит от радиуса (H=2pr l), что приводит к изменению градиента температуры.
Для нахождения количества теплоты, проходящего через цилиндрическую поверхность величиной Н в единицу времени, можно воспользоваться законом Фурье
Подставляя значение градиента температуры и поверхности, получаем
Из уравнения (4.32) следует, что количество теплоты, проходящее через цилиндрическую стенку в единицу времени, полностью определяется заданными граничными условиями. Тепловой поток (4.32) может быть отнесен либо к единице длины трубы, либо к единице внутренней или внешней поверхности. Расчетная формула для плотности теплового потока, проходящего через единицу длины трубы, запишется:
Тепловой поток, отнесенный к единице трубы, измеряется в Вт/м и называется линейной плотностью теплового потока. Как видно из уравнения (4.33), при неизменном отношении d2/d линейная плотность теплового потока не зависит от поверхности цилиндрической стенки. Тепловой поток через единицу внутренней поверхности запишется:
Тепловой поток через единицу наружной поверхности запишется:
На основании полученного уравнения теплового потока на единицу длины трубы (4.33) можно получить уравнение теплового потока многослойной цилиндрической стенки. В этом случае необходимо выразить разности температур слоев из указанного уравнения, а затем, аналогично примеру с плоской стенкой, сложить полученные результаты. В результате получаем уравнение теплового потока многослойной цилиндрической стенки:
Величина, стоящая в знаменателе, называется полным термическим сопротивлением многослойной цилиндрической стенки. Уравнение (4.36) может быть использовано для определения температур на границах любого слоя:
Таким образом, полученные уравнения температурного поля и теплового потока позволяют определить температуры в любой требуемой точке тела (пластины или цилиндра) и определить величину теплового потока. Температурное поле для шаровой стенки имеет вид
Тепловой поток определяется по уравнению
Указанные уравнения можно использовать для расчета температур в агрегатах и узлах автомобиля. Например, распределение температур по толщине двигателя или стенки кабины можно считать по уравнениям плоских стенок; карданных валов — по уравнениям цилиндрических стенок; заднего моста, главной передачи — по уравнениям шаровых стенок. КОНВЕКТИВНЫЙ ТЕПЛООБМЕН 4.3.1. Основные понятия и определения Конвективный теплообмен ¾ это процесс передачи теплоты между твердой поверхностью и окружающей средой, который осуществляется через ламинарный пограничный слой, образующийся в любом случае, а в остальном объеме перенос теплоты осуществляется конвекцией. Различают два вида конвекции: свободную (естественную) и вынужденную. При свободной конвекции жидкость движется за счет разности плотностей, при вынужденной ¾ за счет внешних сил (насос, вентилятор, ветер). Основным уравнением конвективного теплообмена в любом случае является уравнение Ньютона, сводящееся к утверждению, что количество теплоты пропорционально поверхности Н и разности температур Dt:
Q=aH(t1 - t2), (4.40) где a ¾ коэффициент пропорциональности ¾ коэффициент теплоотдачи (Вт/(м2×К)), характеризует величину удельного теплового потока, передаваемого единицей поверхности при градиенте в один градус. Коэффициент теплоотдачи можно представить в виде
где D — толщина ламинарного пограничного слоя. В этом случае оказывается, что a зависит от большого количества факторов — аналогично D — и не имеет аналитического решения. Определение коэффициента теплоотдачи осуществляется экспериментально и это сообщает всему учению о конвективном теплообмене эмпирический характер. Применение теории подобия и теории размерностей дает возможность обобщить опытные данные и свести задачу конвективного теплообмена к зависимости параметров гидродинамического и теплового подобия и этим все учение о конвективном теплообмене приобретает полуэмпирический характер. Теория размерностей Теория размерностей используется в том случае, когда нет дифференциального уравнения, описывающего данный процесс. В условиях вынужденной конвекции величина коэффициента теплоотдачи является функцией по крайней мере шести независимых переменных: весовой скорости u, кг/(м2×с); линейного размера l; вязкости m, кг/(м×с); теплоемкости С, Дж/(кг×К); плотности r, кг/м3 и теплопроводности l, Вт/(м×К). При экспериментальном определении a Вт/(м2×К) необходимо исследовать зависисмость a от шести переменных и провести число опытов a = a(u, l, m, С, r, l). (4.42) Полный дифференциал a равен:
Для перехода к безразмерным (относительным) величинам необходимо иметь переменные, не отсчитываемые от постоянного «нулевого» уровня. Разделим полученное уравнение на a и одновременно делим и умножаем каждое слагаемое на соответствующие значения (l / l; u/u; m/m и т. д.), тогда
Считаем, что соотношения частных производных являются постоянными:
тогда получим
Интегрируем полученное выражение: ln a=iu ln u+i l ln l +…+il ln l+ln C0. (4.46) Потенцируем и получим
Необходимым условием общности полученного решения должно быть требование безразмерности постоянной С0 или ее обратной величины:
Это уравнение не зависит от системы единиц, а в связи с тем, что С0 является безразмерной, то все единицы измерений (справа) должны входить в это уравнение в «0» степени. Для исключения размерностей составим табл. 2.1. Таблица 4.1 Размерности и показатели степени при конвективном Теплообмене
Размерности | ||||||||||||||||||||
| кг | м | с | ° К | Дж | |||||||||||||||||
| 1 | l | i l | - | 1 | 0 | 0 | 0 | ||||||||||||||
| 2 | u | i u | 1 | -2 | -1 | 0 | 0 | ||||||||||||||
| 3 | m | im | 1 | -1 | -1 | 0 | 0 | ||||||||||||||
| 4 | r | ir | 1 | -3 | 0 | 0 | 0 | ||||||||||||||
| 5 | l | il | 0 | -1 | -1 | -1 | 1 | ||||||||||||||
| 6 | С | ic | -1 | 0 | 0 | -1 | 1 | ||||||||||||||
| 7 | a | -1 | 0 | -2 | -1 | -1 | 1 | ||||||||||||||
Исключаем размерности:
1 — (кг) iu + im + ir - ic = 0
2 — (м) i l - 2iu - im - 3ir - il+ 2 = 0
3 — (c) - i l -im - il+ 1 = 0
4 — (°К) - il - ic + 1 = 0
5 — (Дж) il + ic - 1 = 0.
Как видно из последних двух уравнений, полученных исключением размерности, они тождественны, т. к. определяются из теплоемкости воды. Таким образом, имеем 4 независимых уравнения связи при шести независимых переменных. Следовательно, в исходной системе уравнений только два неизвестных показателя подлежат экспериментальному определению, а остальные определяются по полученной системе уравнений в зависимости от этих двух основных. Например, в опыте определены показатели и они соответственно равны: iu= n; ic = m (n, m — число); тогда, используя систему уравнений, получим:
из 4 — il= 1 - ic= 1 - m
из 3 — im = - iu - il + 1 = -n + 1 + m - 1 = m - n
из 1 — ir = ic - iu - im = m - n - m + n = 0
из 2 — i l = 2iu + im + il + 3ir - 2 = 2n + m - n +1 - m - 2 = n - 1.
Подставив полученные значения показателей в (4.48), получим
 (4.49)
(4.49)
Преобразуем полученные уравнения, сгруппировав величины с одинаковыми показателями
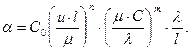 (4.50)
(4.50)
или
 , (4.51)
, (4.51)
где u l /μ = ω l /ν = Re — критерий Рейнольдса — критерий гидродина-мического подобия;
μС/λ = ν/a = Pr — критерий Прандтля — критерий теплофизического подобия;
α l /λ = Nu — критерий Нуссельта — критерий теплового подобия.
Таким образом, на основании теории размерностей получено уравнение связи безразмерных параметров, характеризующих теплообмен в условиях вынужденной конвекции и число независимых переменных снижено с 6 до 2, что обеспечивает возможность их экспериментального определения, и тогда N=An=100.
Правильность использования теории размерностей подтверждается π-теоремой, исходя из чего физическое уравнение, содержащее n³2 размерных величин, из которых m³1 имеют независимые размерности, после приведения их к безразмерному виду должно содержать n безразмерных параметров n = n – m. В нашем случае n = n – m = 6 – 4 = 2. Численные значения постоянных, входящих в уравнение (4.51) С0, n, m, определяются экспериментально и в зависимости от вида теплообмена приводятся в справочной литературе, некоторые даны в табл. 4.3.
|
|
Теория подобия
При использовании теории подобия необходимо иметь дифференциальное уравнение, описывающее исследуемый процесс. Проводя критериальную обработку этого уравнения, получают состав критериев подобия. Выявление состава критериев подобия осуществляется методом «губки»: в исходном дифференциальном уравнении опускаются знаки дифференциалов, полученные результаты приравниваются, выделяются независимые слагаемые, на основании которых определяются параметры подобия.
Для конвективного теплобмена (его математического описания) необходимо иметь: 1) дифференциальное уравнение движения вязкой несжимаемой жидкости — уравнение Навье — Стокса; 2) уравнение теплопроводности — Фурье — Кирхгофа; 3) уравнение теплообмена на границе твердая поверхность — окружающая среда — Био —Фурье.
Уравнение движения вязкой несжимаемой жидкости:
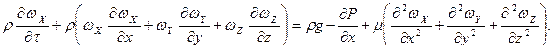 (а)
(а)
Получаем на основании теории подобия с использованием метода «губки» 5 независимых комплексов (уравнение написано для одномерного потока по оси «Х»).
| № п/п | 1 | 2 | 3 | 4 | 5 |
| комплексы | 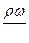
| 
| 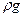
| 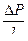
| 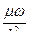
|
Группируем полученные независимые комплексы и получаем критерии подобия:
делим 2:1 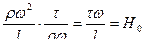 ; (4.52)
; (4.52)
2:5 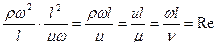 ; (4.53)
; (4.53)
4:2 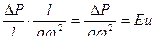 ; (4.54)
; (4.54)
3:2 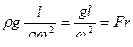 , (4.55)
, (4.55)
где Но — критерий гомохронности — гидродинамический критерий одновременности событий;
Re — критерий Рейнольдса — параметр гидродинамического подобия режимов движения жидкости, характеризует соотношение сил инерции и сил вязкости;
Eu — критерий Эйлера — характеризует соотношение сил инерции и сил давления;
Fr — критерий Фруда — характеризует соотношение сил инерции и сил тяжести.
Следует отметить, что полученный основной состав критериев подобия Но, Re, Eu, Fr характеризует режим движения потока и может быть преобразован в любой иной состав критериев подобия умножением или делением исходного состава, но при этом в любом случае должно выполняться условие по возврату любого иного состава критериев подобия к исходному.
Так, вместо критерия Фруда можно использовать критерий Галилея:
 (4.56)
(4.56)
или
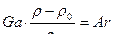 , если
, если 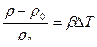 , то (4.57)
, то (4.57)
 (4.58)
(4.58)
Умножая критерий Ga на относительное изменение плотности (ρ – ρ0/ρ0), получим критерий Архимеда. Если ρ – ρ0/ρ0 = βΔТ происходит за счет разности температур ΔТ = Т1 – Т2, то получим критерий Грасгофа. Критерий Ar характеризует величину подъемной силы при изучении свободной конвекции жидкости, в которой находятся пузырьки, твердые частицы или капли другой жидкости. Критерий Ga используется вместо критерия Fr, т. к. в него входит скорость потока, которую трудно измерить.
Кроме того, оказывается, что часть критериев является зависимой — функцией других критериев. Так, критерий Eu зависит от Re, что получается из рассмотрения уравнения Дарси — Вейсбаха:

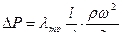 , (4.59)
, (4.59)
откуда
 , (4.60)
, (4.60)
с другой стороны
 . (4.61)
. (4.61)
Вторым уравнением, описывающим процесс конвективного теплообмена при вынужденном движении, является уравнение теплопроводности
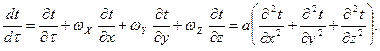 (б)
(б)
Применяя метод «губки», получим три независимых комплекса:
делим 2:3  ; (4.62)
; (4.62)
3:1  . (4.63)
. (4.63)
| № п/п | 1 | 2 | 3 |
| комплексы | 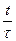
| 
| 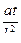
|
Получаем критерии Пекле Pe и Фурье Fо. Критерий Pe характеризует соотношение тепловых потоков, переносимых конвекцией и теплопроводностью. Вместо критерия Pe можно использовать критерий Прандтля, т. к.
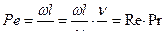 . (4.64)
. (4.64)
Критерий Fо характеризует одновременность событий, так называемое безразмерное время. Из третьего уравнения теплообмена на границе твердая поверхность — окружающая среда получим критерий теплового подобия — критерий Нуссельта Nu:
 (в)
(в)
| № п/п | 1 | 2 |
| комплексы | 
| 
|
делим 2:1 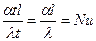 . (4.65)
. (4.65)
Таким образом, проведя критериальную обработку дифференциальных уравнений, получим состав критериев подобия:
Nu=¦(Ho, Fo, Re, Pe, Gr)=¦1(Ho, Fo, Re, Pe, Gr). (4.66)
Связь между критериями определяется опытным путем. Следует заметить, что теории размерностей и подобия могут использоваться при изучении любых процессов (гидравлических, механических, экономических).
В табл. 4.2 приводятся критерии тепловых и гидродинамических процессов.
Таблица 4.2
Главнейшие безразмерные критерии тепловых и гидродинамических процессов
| Формула | Название критерия | Величины, входящие в критерий | Значение критерия |
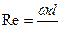
| Критерий Рейнольдса (критерий режима движения) | w - скорость потока, м/сек; d - эквивалентный диаметр канала; n - коэффициент кинематической вязкости, м2/сек. | Характеризует гидродинамический режим движения |
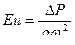
| Критерий Эйлера (критерий падения давления) | DР - перепад давления, Н/м2; r - плотность жидкости, кг/м3. | Характеризует безразмерную величину падения давления |
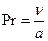
| Критерий Прандтля (критерий физических свойств жидкости) | Характеризует физические свойства жидкости и способность распространения тепла в жидкости | |
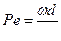
| Критерий Пекле | Является мерой отношения молекулярного и конвективного переноса тепла в потоке | |
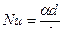
| Критерий Нуссельта (критерий теплоотдачи) | a - коэффициент конвективной теплоотдачи, Вт/(м2×град) | Характеризует отношение между интенсивностью теплоотдачи и температурным полем в пограничном слое потока |
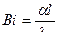
| Критерий Био | l - характерный размер тела, м; lм - коэффициент теплопроводности твердого тела, Вт/(м×град) | Характеризует соотношение между внутренним и внешним термическим сопротивлениями |
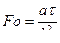
| Критерий Фурье (безразмерное время) | t - время, сек | Характеризует связь между скоростью изменения температурного поля, физическими константами и размерами тела |
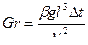
| Критерий Грасгофа (критерий подъемной силы) | b - коэффициент объемного расширения, 1/град; Dt - разность температур в двух точках системы потока и стенки, град | Характеризует кинематическое подобие при свободном движении жидкости |
Критериальные уравнения
При установлении функциональной связи между коэффициентом теплоотдачи и параметрами конвективного теплообмена можно перейти от размерных функций к безразмерным и тогда, используя эксперимент, определять функции типа
Nu=¦(Re, Pr, Gr, Fo). (4.67)
Формула (4.67) называется критериальным уравнением. Количество переменных (которыми здесь являются критерии подобия), входящих в такую зависимость, всегда значительно меньше, чем в случае установления зависимости в размерном виде. Имея конкретный вид функции (4.67), легко определить величину коэффициента теплоотдачи. Вычисление критериев подобия Re, Pr, Gr и др. не представляет значительных трудностей.
Практическое использование критериальных уравнений и в тепловых расчетах ДВС заключается в определении с их помощью коэффициента теплоотдачи:
 (4.68)
(4.68)
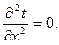 (4.22)
(4.22)
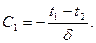
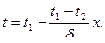 (4.25)
(4.25)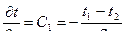 , получим
, получим 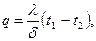
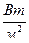 . (4.26)
. (4.26)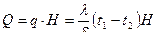 , Вт. (4.27)
, Вт. (4.27)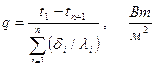 . (4.28)
. (4.28)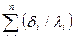 называется полным термическим сопротивлением теплопроводности многослойной стенки.
называется полным термическим сопротивлением теплопроводности многослойной стенки.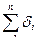 , а термическое сопротивление равно термическому сопротивлению рассматриваемой стенки, т.е.:
, а термическое сопротивление равно термическому сопротивлению рассматриваемой стенки, т.е.: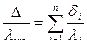 .
.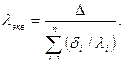 (4.29)
(4.29)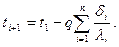 (4.30)
(4.30)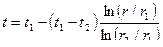
 . (4.31)
. (4.31)
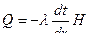 .
. , Вт. (4.32)
, Вт. (4.32)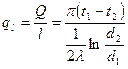 , Вт/м. (4.33)
, Вт/м. (4.33)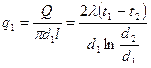 , Вт/м. (4.34)
, Вт/м. (4.34)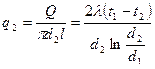 , Вт/м. (4.35)
, Вт/м. (4.35) , Вт/м. (4.36)
, Вт/м. (4.36)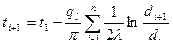 . (4.37)
. (4.37)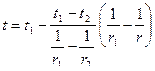 . (4.38)
. (4.38)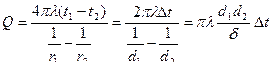 , Вт. (4.39)
, Вт. (4.39)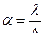 , (4.41)
, (4.41) , где А — число опытов с одной переменной, например, А = 10; n — число независимых переменных. Для данного примера оказывается, что число опытов равно одному миллиону, что является совершенно нереальным. Применение же теории размерностей приводит к сокращению независимых переменных. В условиях вынужденной конвекции коэффициент теплоотдачи является функцией
, где А — число опытов с одной переменной, например, А = 10; n — число независимых переменных. Для данного примера оказывается, что число опытов равно одному миллиону, что является совершенно нереальным. Применение же теории размерностей приводит к сокращению независимых переменных. В условиях вынужденной конвекции коэффициент теплоотдачи является функцией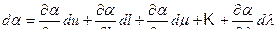 . (4.43)
. (4.43)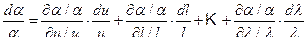 . (4.44)
. (4.44)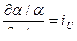 ;
; 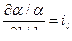 ; …;
; …; 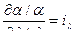 ,
,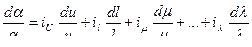 . (4.45)
. (4.45)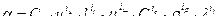 . (4.47)
. (4.47)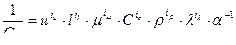 . (4.48)
. (4.48)


