Раздел 1. Моделирование в экономике.

РАЗДЕЛ 1. МОДЕЛИРОВАНИЕ В ЭКОНОМИКЕ.

ПОЧЕМУ НЕОБХОДИМО ИСПОЛЬЗОВАНИЕ МАТЕМАТИКИ В ЭКОНОМИКЕ?

 

Современная экономическая теория, как на микро-, так и на макроуровне, включает как естественный, необходимый элемент математические модели и методы. Использование математики в экономике позволяет, во-первых, выделить и формально описать наиболее важные, существенные связи экономических переменных и объектов: изучение столь сложного объекта предполагает высокую степень абстракции. Во-вторых, из четко сформулированных исходных данных и соотношений методами дедукции можно получать выводы, адекватные изучаемому объекту в той же мере, что и сделанные предпосылки. В-третьих, методы математики и статистики позволяют индуктивным путем получать новые знания об объекте: оценивать форму и параметры зависимостей его переменных, в наибольшей степени соответствующие имеющимся наблюдениям. Наконец, в-четвертых, использование языка математики позволяет точно и компактно излагать положения экономической теории, формулировать ее понятия и выводы.

 

Математические модели использовались с иллюстративными и исследовательскими целями еще Ф. Кенэ (1758 г., «Экономическая таблица»), А. Смитом (классическая макроэкономическая модель), Д.Рикардо (модель международной торговли). В XIX веке большой вклад в моделирование рыночной экономики внесла математическая школа (Л. Вальрас, О. Курно, В. Парето, Ф.Эджворт и др.). В XX веке математические методы моделирования применялись очень широко, с их использованием связаны практически все работы, удостоенные Нобелевской премии по экономике (Д. Хикс, Р. Солоу, В. Леонтьев, П. Самуэльсон и др.). Развитие микроэкономики, макроэкономики, прикладных дисциплин связано со все более высоким уровнем их формализации. Основу для этого заложил прогресс в области прикладной математики - теории игр, математического программирования, математической статистики. В России в начале XX века большой вклад в математическое моделирование экономики внесли В.К. Дмитриев и Е.Е. Слуцкий. В 1960-е - 80-е годы экономико-математическое направление возродилось (В.С. Немчинов, В.В. Новожилов, Л.В. Канторович), но было связано в основном с попытками формально описать «систему оптимального функционирования социалистической экономики» (СОФЭ, Н.П. Федоренко, С.С. Шаталин и др.). Строились многоуровневые системы моделей народнохозяйственного планирования, оптимизационные модели отраслей и предприятий.

 

Любое экономическое исследование всегда предполагает объединение теории (экономической модели) и практики (статистических данных). Мы используем теоретические модели для описания и объяснения наблюдаемых процессов и собираем статистические данные с целью эмпирического построения и обоснования моделей.

 

ЭКОНОМИЧЕСКИЕ МОДЕЛИ. ПОНЯТИЕ ЭКОНОМИЧЕСКОЙ МОДЕЛИ.

 

Для изучения различных экономических явлений экономисты используют их упрощенные формальные описания, называемые экономическими моделями. Примерами экономических моделей являются модели потребительского выбора, модели фирмы, модели экономического роста, модели равновесия на товарных, факторных и финансовых рынках и многие другие. Строя модели, экономисты выявляют существенные факторы, определяющие исследуемое явление и отбрасывают детали, несущественные для решения поставленной проблемы. Формализация основных особенностей функционирования экономических объектов позволяет оценить возможные последствия воздействия на них и использовать такие оценки в управлении.

 

МАТЕМАТИЧЕСКАЯ СТРУКТУРА МОДЕЛИ И ЕЕ СОДЕРЖАТЕЛЬНАЯ ИНТЕРПРЕТАЦИЯ.

 

ПРИМЕР 1.

 

Пусть требуется определить, какую сумму следует положить в банк при заданной ставке процента (20% годовых), чтобы через год получить $12000?

 

Вводя формальные обозначения для величин, фигурирующих в задаче:

 

начальная сумма денег - М0,

 

конечная сумма денег - М1,

 

ставка процента — R,

 

и записывая соотношение между ними:

 

М1 = М0(1+ R/100),

 

найдем требуемую величину из решения основного уравнения модели:

 

М0 = М1/(1+ R/100) = $12000/1,2 = $10000.

ПРИМЕР 2.

Пусть требуется определить, каков был объем выпуска продукции завода, если в результате технического перевооружения средняя производительность труда увеличилась на 20%, и завод стал выпускать 12000 единиц продукции.

 

Вводя формальные обозначения для величин, фигурирующих в задаче:

 

начальный выпуск - Q0,

 

конечный выпуск - Q1,

 

процент прироста производительности - R,

 

и записывая соотношение между ними (следующее из определения средней производительности труда Q/L):

 

Q1=Q0 L1/L0 = Q0(1+ (L1-L0)/L0)=Q0(1+R/100),

найдем искомую величину из решения основного уравнения модели

 

Q0 = 12000/1,2=10000.

Сравнивая полученные модели и результаты, мы можем заметить, что математическая форма модели:

 

X1=X0(1+R/100)

 

и даже числовые значения входящих в нее величин в обоих случаях одинаковы, однако экономическая ситуация, описываемая моделью, экономическая интерпретация модели и результатов расчета совершенно различны. Таким образом, одни и те же математические модели и методы могут быть использованы для решения совершенно различных экономических задач.

 

ПРИМЕР 3. (П ОСТРОЕНИ Е МАТЕМАТИЧЕСКОЙ МОДЕЛИ ЭКОНОМИЧЕСКОГО ОБЪЕКТА).

 

Рассмотрим пример экономико-математической модели задачи (о диете или рациональных смесях) формирования экономного суточного набора продуктов питания.

 

Введем следующие обозначения:

 

m — количество питательных веществ;

 

n — количество продуктов питания;

 

cj - цена 1 кг j-го продукта, руб.;

 

zj — запас j-го продукта, кг;

 

qi - i-е питательное вещество;

 

bi - норма суточной потребности в i-м питательном веществе, г;

qij - вес i-го питательного вещества в 1 кг j-продукта, г;

 

xj — вес j-го продукта в общем наборе питания, кг;

 

С - общие затраты на питание, руб.

 

Взаимосвязи между перечисленными показателями задачи формально можно записать в обобщенном виде таким образом:

 

С = f(cj, zj, qi, bi, qij, xj, m, n) → min,

 

или в виде математических уравнений, неравенств и систем уравнений, что в сочетании с содержательной частью задачи имеют следующий вариант постановки:

Найти оптимальные величины веса каждого продукта питания в общем наборе

 

x1=?, x2 =?, …, xn =?

 

при следующих ограничениях:

 

вес каждого питательного вещества в наборе должен быть более или равен суточной норме потребления человека:

 

qi1x1 + qi2x2 + … + qinxn ≥ bi, i = 1, …, m;

 

причем каждый продукт должен входить в диету и, кроме того, его вес не должен превышать величины имеющегося запаса:

 

0 < xj ≤ zj, j = 1, …, n;

 

а стоимость набора продуктов при этом должна быть наименьшей:

 

С= c1x1 + c2x2 + … + cnxn → min.

Записанные уравнения и неравенства — совокупность, которая представляет собой экономико-математическую модель задачи. Решение этой задачи можно получить с помощью, например, методов линейного программирования.

 

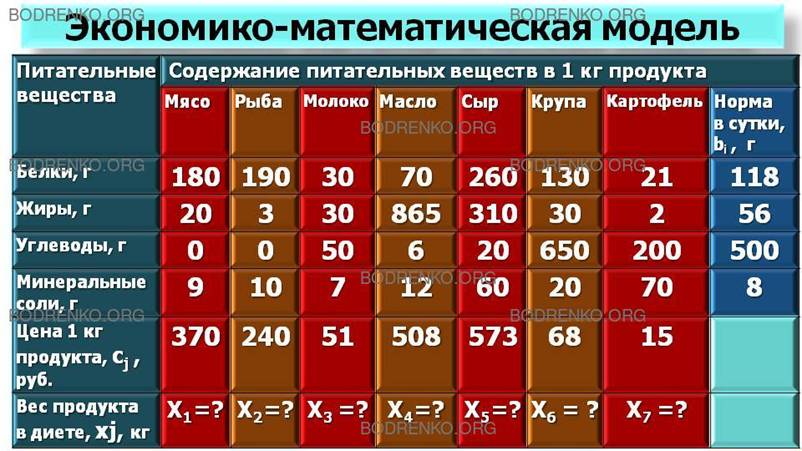
Экономико-математическую модель этой же задачи можно представить еще и в матричном виде. Например, для поддержания нормальной жизнедеятельности человеку ежедневно необходимо потреблять белки, жиры, углеводы, минеральные соли. Количество питательных веществ, содержащихся в 1 кг имеющихся продуктов питания, а также их стоимость и нормы суточной потребности питательных веществ изображены в виде матрицы (таблица 1).

 

Таблица 1.

 

Питательные вещества	Содержание питательных веществ в 1 кг продукта
	Мясо	Рыба	Молоко	Масло	Сыр	Крупа	Картофель	Норма в сутки, bi, г
Белки, г	180	190	30	70	260	130	21	118
Жиры, г	20	3	30	865	310	30	2	56
Углеводы, г	0	0	50	6	20	650	200	500
Минеральные соли, г	9	10	7	12	60	20	70	8
Цена 1 кг продукта, cj, руб.	370	240	51	508	573	68	15
Вес продукта в диете, xj, кг	X1=?	X2 =?	X3 =?	X4 =?	X5 =?	X6 =?	X7 =?

Требуется составить дневной рацион продуктов питания, содержащий не менее суточной нормы потребности человека в необходимых питательных веществах и обеспечивающий минимальную общую стоимость продуктов.

 

Экономико-математическая формулировка и модель этой задачи имеют следующий вид:

 

Найти оптимальный вес имеющихся продуктов питания при ограничениях, связанных с суточной нормой потребления, записанных в виде системы неравенств:

 

180x1 +190x2 +30x3 +70x4+260x5 +130x6 +21x7 ≥ 118,

 

20x1 +3x2 +40хз +865x4 +310x5 +30х6 +2x7 ≥ 56,

 

0x1 + 0x2 +50хз +6x4 +20x5 +650x6 +200x7 ≥ 500,

 

9x1 +10x2 +7x3 +12x4 +60x5 +20х6 +70x7 ≥ 8,

 

x1 > 0, x2 > 0, x3 > 0, x4 > 0, x5 > 0, x6 > 0, x7 > 0;

 

решение которой позволяет определить минимум затрат на продукты питания:

 

С= (370x1 + 240x2 + 51x3 + 508x4 + 573x5 + 68х6 + 15x7) → min.

Дальнейшим развитием задачи о рациональном питании являются постановки и решения задач, связанных с товароснабжением и управлением товарными запасами на коммерческих предприятиях. Задача управления товарными запасами связана с поиском ответов на следующие вопросы: кому, когда и в каком объеме заказывать товары; какой лучший маршрут перевозки товаров; каким транспортом перевозить: автомобильным, железнодорожным или воздушным; какая частота и величина поставок товара?

 

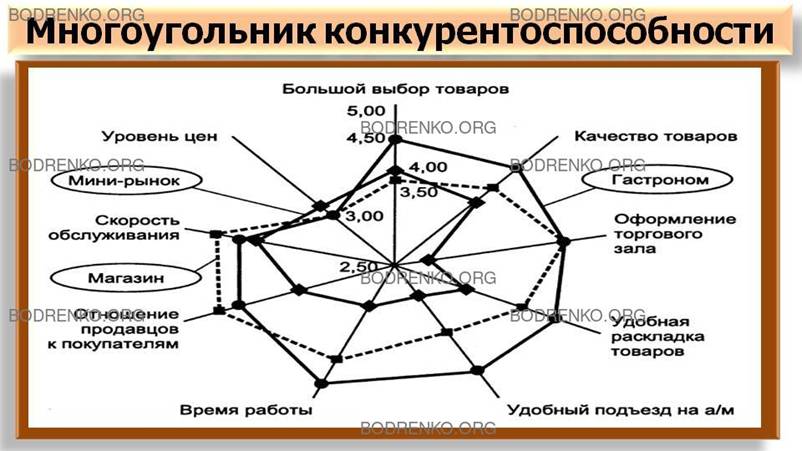
Интересной моделью является многоугольник конкурентоспособности (рисунок 1), показывающий соотношение различных показателей на плоскости, иногда его называют радаром или полигоном по аналогии с экраном радиолокатора. По каждой оси для отображения уровня значений каждого из исследуемых факторов используется определенный масштаб измерений, часто в виде балльных оценок. Изображая на одном рисунке многоугольники конкурентоспособности для разных предприятий, можно провести анализ уровня их конкурентоспособности по разным факторам.

 

Рисунок 1. Многоугольник конкурентоспособности.

 

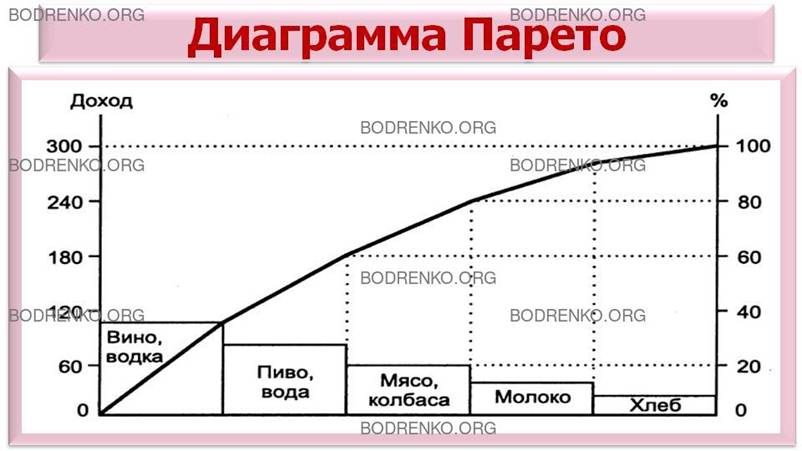
Для выявления наиболее вероятных или проблемных задач, на которых следует сосредоточить усилия фирмы, необходимо сравнить несколько факторов, влияющих на интересующий показатель коммерческой деятельности. Для этого можно использовать диаграммы относительной важности, получаемые, например, методами экспертных оценок. Графики такого вида (рисунок 2) называют диаграммами Парето, по имени итальянского экономиста.

Рисунок 2. Диаграмма Парето.

 

ЧТО ИЗУЧАЕТ ЭКОНОМЕТРИКА?

Эконометрика - наука, исследующая количественные закономерности и взаимозависимости в экономике при помощи методов математической статистики. Основа этих методов — корреляционно- регрессионный анализ. Использование современных методов математической статистики началось в биологии. В последней четверти XIX века английский биолог К. Пирсон положил начало современной математической статистике изучением кривых распределения числовых характеристик человеческого организма. Затем он и его школа перешли к изучению корреляций в биологии и построению линейных функций регрессии. Первые работы по эконометрике появились в конце XIX - начале XX века. В 1897 г. появилась работа одного из основателей математической школы в экономической теории В. Парето, посвященная статистическому изучению доходов населения в разных странах. Была предложена кривая Парето: y =A (x - a)^-α, где x -величина дохода; у - численность лиц, имеющих доход, больший x, а- минимальный доход; A и α - параметры зависимости, получаемые статистическими методами.

 

В самом начале XX века вышло несколько работ английского статистика Гукера, в которых он применил корреляционно-регрессионные методы, разработанные Пирсоном и его школой, для изучения взаимосвязей экономических показателей, в частности - влияния числа банкротств на товарной бирже на цену зерна. В работах Гукера содержалась идея временного лага между экономическими переменными, а также идея корреляционного анализа не самих величин, а их приращений. В дальнейшем появилось огромное число работ как по развитию теории математической статистики и ее прикладных элементов, так и по практическому приложению этих методов в экономическом анализе. К первой группе могут быть, например, отнесены работы Р. Фишера по дисперсионному анализу, ко второй - работы по оценке и исследованию производственных функций, в частности - классическая работа Кобба и Дугласа 1928 года.

 

Производственной функцией является математическая модель вида

 

y = f (x1, x2, …, xi, …, xn),

 

описывающая зависимость, например, объема продажи продукции от величины ресурсов разного вида, в качестве которых выступают трудовые ресурсы, торговые площади, товарные запасы, рабочее время и др.

 

Наиболее типичными производственными функциями являются степенные модели вида:

 

y = a0 П{i=1,..., n} xi ^ai,

 

одним из вариантов которой является производственная функция Кобба-Дугласа:

 

у= a0 x1 ^a1 x2 ^a2

Функцией производственных затрат является модель вида

 

x1 = h (y1, y2, …, ym),

 

которая описывает зависимость затрат какого-либо ресурса X1, например, от объема продажи товаров y1, y2, …, ym всего ассортимента.

В общем виде функции потребления представляют собой многофакторную модель связи уровня потребления материального блага S и факторов влияния u1, u2, …, un, определяющих спрос и потребление, что можно записать так:

 

S = f (u1, u2, …, ui, …, un).

 

Шведский экономист Л. Торнквист предложил три вида однофакторных моделей связи объема потребления S (спроса) от уровня u - дохода:

 

для предметов первой необходимости —

 

S1 = a0 u/(a1 + u);

 

для менее необходимых предметов -

 

S2 = a0(u — a1)/(u + a2);

 

для предметов роскоши —

 

S3 = a0 u (u — a1)/(u + a2).

Эконометрические модели и методы сейчас - это не только мощный инструментарий для получения новых знаний в экономике, но и широко применяемый аппарат для принятия практических решений в прогнозировании, банковском деле, бизнесе.

 

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.

 

[1] Замков О.О., Толстопятенко А.В., Черемных Ю.М. Математические методы в экономике: Учебник. 2-е изд. - М.: МГУ им. М.В. Ломоносова, Издательство «Дело и Сервис», 1999. — 368 с.

 

[2] Фомин Г. П. Математические методы и модели в коммерческой деятельности: Учебник. — 2-е изд., перераб. и доп. — М.: Финансы и статистика, 2005. — 616 с: ил.

 

[3] Шелобаев С. И. Математические методы и модели в экономике, финансах, бизнесе: Учеб. пособие для вузов. — М.: ЮНИТИ - ДАНА, 2001. - 367 с.

[4] Шикин Е. В., Чхартишвили А. Г. Математические методы и модели в управлении: Учеб. пособие. — 3-е изд. — М.: Дело, 2004. — 440 с. — (Серия «Классический университетский учебник»).

[5] Экономико-математические методы и прикладные модели: Учебное пособие для вузов/ В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др.; Под ред. В.В. Федосеева. — М.: ЮНИТИ, 1999. - 391 с.

 

 

РАЗДЕЛ 1. МОДЕЛИРОВАНИЕ В ЭКОНОМИКЕ.