
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод замены переменнойили метод подстановки
Суть метода заключается в том, что часть подынтегрального выражения обозначают новой переменной и выражают через нее дифференциал и оставшуюся часть подынтегрального выражения. Осуществляют подстановку такой замены под интеграл, после чего подынтегральное выражение должно упроститься и интеграл можно привести к табличному виду. Обращаем внимание на то, что не всегда есть необходимость записывать оставшуюся часть подынтегрального выражения через новую переменную. Часто ее можно оставить в исходном виде, после подстановки она сокращается. Если это не происходить, тогда нужно выражать через новую переменную и ее. Но обязательно выражать через новую переменную дифференциал! После того, как интеграл решен относительно новой переменной, возвращаются к исходной переменной и записывают ответ через нее. Возможны случаи, когда после первой замены подынтегральное выражение упрощается, но полученный таким образом интеграл не удается привести к табличному виду, и потребуется еще замена с использованием другой переменной или решение иным способом. Рассмотрим примеры. Пример 1. Обозначим выражение
Подставим замены под интеграл, найдем его и вернемся к исходной переменной
Пример 2. Обозначим выражение
Подставим замены под интеграл, найдем его и вернемся к исходной переменной
Пример 3. Обозначим выражение
Подставим замены под интеграл: Видим, что сейчас под интегралом стоят две переменные. Выразим из первоначальной замены
В этом случае решение интеграла отличается от предыдущих случает, так как потребует использование не только замены переменной, но и использования формулы дифференциала функции. Итак, сначала преобразуем подынтегральное выражение, помножив числитель и знаменатель на
Теперь используем формулу дифференциала функции:
Теперь введем подстановку:
Пример 5. Обозначим
Подставим замены под интеграл:
Решение интеграла по частям Метод интегрирования по частям вытекает из правил дифференцирования и свойств неопределенных интегралов. Возьмем произведение двух функций
Проинтегрируем обе части последнего равенства:
Используя свойство 2 неопределенных интегралов, имеем
Эту формулу называют формулой интегрирования по частям. Суть метода интегрирования по частям заключается в том, что часть подынтегрального выражения, не содержащую дифференциал переменной, обозначают через функцию Рассмотрим примеры интегрирования по частям. Пример 1. Введем обозначения функции
После применения формулы интегрирования по частям получили интеграл более сложный, чем исходный. Это значит, что наша замена была неудачной. Не целесообразно степенную функцию (у нас это
Введем другую замену:
Пример 2.
Замена опять проведена неудачно. Опять увеличился показатель степенной функции, но, кроме этого, под интегралом осталась тригонометрическая функция. Функция Введем другую замену:
Пример 3.
Видим, что подынтегральное выражение упростилось (понизился показатель степенной функции). Чтобы совсем вывести степенную функцию из под интеграла, решим новый интеграл также по частям:
Пример 4.
Пример 5. Видим, что в этом примере под интегралом стоят функции
Теперь полученный интеграл также по частям с теми же заменами:
Объедим исходный интеграл и полученный результат:
Заметим, что в левой и правой частях этого равенства стоят одинаковые интегралы. Перенесем их в одну часть и сложим, как подобные слагаемые:
Таким образом, не имея возможности вычислить исходный интеграл, мы сумели найти, чему он будет равен.
|
||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 175; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.226.216 (0.021 с.) |
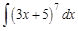
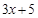 через новую переменную
через новую переменную 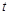 и выразим через нее дифференциал
и выразим через нее дифференциал 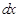 , для чего найдем дифференциалы от обеих частей в полученном выражении:
, для чего найдем дифференциалы от обеих частей в полученном выражении: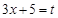
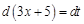
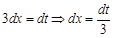
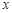 :
: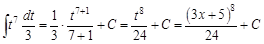
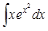
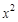 через новую переменную и выразим через нее дифференциал
через новую переменную и выразим через нее дифференциал 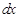 , для чего найдем дифференциалы от обеих частей в полученном выражении:
, для чего найдем дифференциалы от обеих частей в полученном выражении: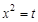
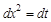
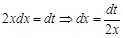
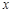 :
: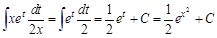

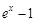 через новую переменную
через новую переменную 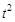 и выразим через нее дифференциал
и выразим через нее дифференциал 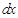 , для чего найдем дифференциалы от обеих частей в полученном выражении:
, для чего найдем дифференциалы от обеих частей в полученном выражении:
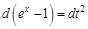
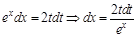
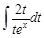 .
.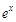 . Получим:
. Получим:  . Подставим это выражение под интеграл:
. Подставим это выражение под интеграл: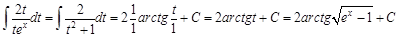 Пример 4.
Пример 4. 
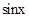 :
: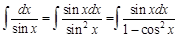 .
.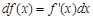 . В числителе под интегралом стоит левая часть этой формулы:
. В числителе под интегралом стоит левая часть этой формулы:  . Тогда
. Тогда 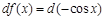 , и мы можем заменить числитель подынтегрального выражение на
, и мы можем заменить числитель подынтегрального выражение на 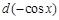 . Получим:
. Получим: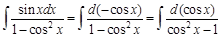 .
. . Тогда:
. Тогда: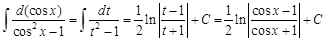 .
.
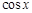 через новую переменную
через новую переменную 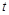 и выразим через нее дифференциал
и выразим через нее дифференциал 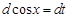
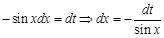

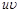 и найдем дифференциал этого произведения:
и найдем дифференциал этого произведения: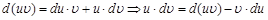
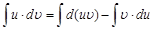
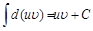 . Тогда получим:
. Тогда получим: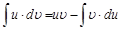
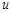 . Тогда оставшаяся часть подынтегрального выражения, в которую входит дифференциал переменной, будет
. Тогда оставшаяся часть подынтегрального выражения, в которую входит дифференциал переменной, будет 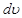 . Согласно формуле интегрирования по частям, еще потребуется найти функцию
. Согласно формуле интегрирования по частям, еще потребуется найти функцию 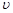 и дифференциал
и дифференциал 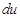 . После чего все величины подставляют, приравнивая исходный интеграл к правой части указанной формулы. При удачном выборе функции
. После чего все величины подставляют, приравнивая исходный интеграл к правой части указанной формулы. При удачном выборе функции 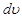 интеграл в правой части упрощается и его можно привести к табличному виду одним из описанных выше способов. Но бывают случаи, когда новый записанный интеграл правой части формулы требуется еще раз взять по частям или применить другой метод интегрирования.
интеграл в правой части упрощается и его можно привести к табличному виду одним из описанных выше способов. Но бывают случаи, когда новый записанный интеграл правой части формулы требуется еще раз взять по частям или применить другой метод интегрирования.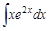
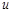 и
и 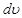 найдем соответственно
найдем соответственно 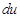 и
и 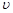 следует каждый раз осуществлять проверку, находя дифференциал от подобранной функции и сравнивая его с
следует каждый раз осуществлять проверку, находя дифференциал от подобранной функции и сравнивая его с 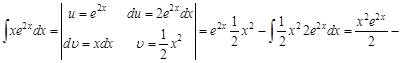
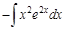 .
.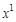 ) вводить в часть выражения, содержащую дифференциал
) вводить в часть выражения, содержащую дифференциал 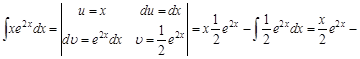
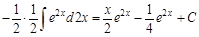 .
.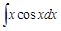
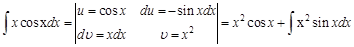 .
.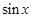 . Работая с функциями
. Работая с функциями  ,
, 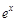 нужно смотреть, в сочетании с какими функциями они стоят в исходном интеграле, и какие замены целесообразно проводить.
нужно смотреть, в сочетании с какими функциями они стоят в исходном интеграле, и какие замены целесообразно проводить.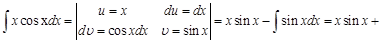
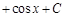
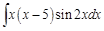
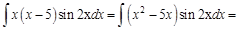
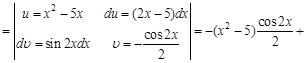
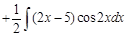
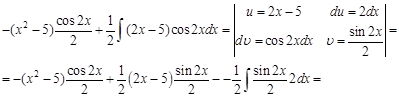
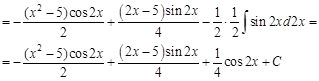
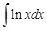
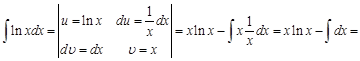
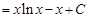
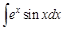
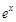 и
и 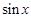 , и какую бы из них мы не обозначали через
, и какую бы из них мы не обозначали через 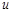 , под интегралом останется
, под интегралом останется 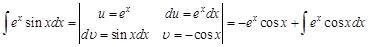 .
.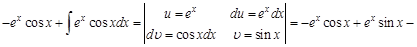
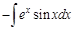 .
.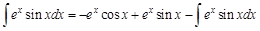 .
.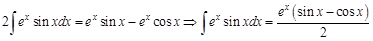 .
.


