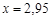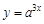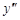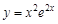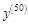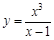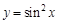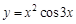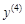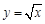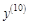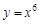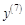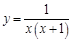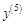Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производные элементарных функций и правила нахождения производных
При нахождении производных функций руководствуются следующими основными правилами дифференцирования. Правило 1. Производная постоянной величины равна нулю. Правило 2. Постоянный множитель можно выносить за знак производной. Правило 3. Производная алгебраической суммы конечного числа дифференцируемых функций равна соответствующей сумме производных этих функций.
Правило 4. Производная произведения двух дифференцируемых функций равна сумме произведений производной первой функции на вторую функцию и первой функции на производную второй функции.
Правило 5. Производная частного двух дифференцируемых функций (при условии, что знаменатель не обращается в ноль) равна дроби, числитель которой представляет собой разность между произведением производной первой функции на вторую функцию и произведением первой функции на производную второй функции, а знаменатель равен квадрату знаменателя данной дроби.
Правило 6. Производная сложной функции. Если
Как определить, что имеем дело со сложной функцией? Если в выражении, от которого ищем производную, независимая переменная встречается только один раз, то функция сложная. Если же независимая переменная встречается более одного раза, то функций несколько, и при нахождении производной сначала следует воспользоваться правилами 3–5. Например, функция При нахождении производных функций следует помнить о порядке выполнения арифметических действий: приоритет перед остальными действиями имеют возведение в степень и извлечение корня (помним, что корни можно заменять степенями), далее рассматривают умножение и деление и в последнюю очередь сложение и вычитание. Исходя из определения производной, вычислены производные элементарных функций.
1) Отметим, что: а) б) при нахождении производных от корней корень заменяют соответствующей степенью и определяют производную от степенной функции
Рассмотрим примеры нахождения производных функций. Пример 1. В этом случае удобно представить дробь в виде суммы дробей, почленно поделив числитель на знаменатель, а затем искать производные от полученных слагаемых.
Пример 2. Распишем выражение по правилу для нахождения производной от произведения функций, далее найдем производные от элементарных функций
Пример 3. Сначала запишем правило для нахождения производной частного, а затем найдем производные элементарных функций.
Пример 4. Здесь мы имеем дело со сложной функцией (независимая переменная
Тогда производную этой сложной функции с учетом приоритета действий можно записать так:
В результате имеем:
Иногда бывает проще понять процесс нахождения производной сложной функции, ассоциируя его с раскрыванием матрешки. Раскрывая внешнюю матрешку, мы оставляем нетронутым все, что у нее внутри. Так же и с отысканием производной сложной функции: сперва найдем производную от внешней функции, опираясь на приоритет арифметических действий, оставив внутренние функции нетронутыми, затем следующую и так до тех пор, пока не дойдем до независимой переменной. При этом все найденные производные перемножаются. В рассмотренном примере это выглядит так:
Результат получили такой же. Пример 5. В этом случае найти производную сразу не удастся. Сначала прологарифмируем выражение, получим:
Рассмотрим примеры нахождения дифференциалов функций. Пример 1. Дифференциал функции находим по формуле
Пример 2.
Умение находить дифференциал функции потребуется при решении интегралов и дифференциальных уравнений.
Рассмотрим пример приблизительного вычисления значений функции. Пример 1. Пусть дана функция Общая формула для приближенных вычислений значений функции имеет вид
Для всех достаточно малых
Тогда значение функции в точке
По полученной формуле произведем приблизительные вычисления. Найдем
Найдем
Производные высших порядков Пусть функция В общем случае n-ой производной функции или производной n-го порядка в точке
Производные порядков выше первого называют производными высших порядков. Порядок таких производных указывают в круглых скобках, чтобы не путать их со степенями функций. Производные высших порядков можно обозначать и через дифференциалы. Например, Рассмотрим примеры нахождения производных высших порядков. Пример 1.
Видим, что эта функция имеет ненулевые производные для первых трех порядков, а производные 4-го и более высоких порядков будут равны нулю. Пример 2.
Заметим, что выражения найденных производных имеют схожие элементы, и можно записать общую формулу для определения производной n-го порядка:
Тогда сотая производная исходной функции будет равна:
Но так красиво бывает далеко не всегда. Довольно часто функция, являющаяся производной очередного порядка, становится более сложной чем та, от которой эту производную нашли. Пример 3.
Как видим, производные более высоких порядков этой функции становятся все более сложными.
1.5. Задания для самостоятельного решения I. Найдите производные функции одной переменной
II. Найдите дифференциалы функций одной переменной
III. Найдите приближенное значение функции
IV. Найдите приближенно числовое значение функции
V. Найдите производные указанных порядков для приведенных функций:
ЧАСТНЫЕ ПРОИЗВОДНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 464; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.8.247 (0.037 с.) |
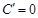 , где
, где 
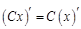 , где
, где 
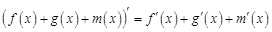 . Обращаем внимание на то, что некоторые слагаемые могут быть отрицательными. Перед ними сохраняется знак минус.
. Обращаем внимание на то, что некоторые слагаемые могут быть отрицательными. Перед ними сохраняется знак минус.
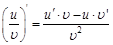
 и
и  – дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу, умноженной на производную самого промежуточного аргумента по независимой переменной.
– дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу, умноженной на производную самого промежуточного аргумента по независимой переменной. или в другой форме записи
или в другой форме записи 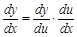 .
. является сложной, независимая переменная
является сложной, независимая переменная 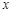 в ней встречается один раз. А функция
в ней встречается один раз. А функция 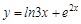 представляет собой сумму двух слагаемых.
представляет собой сумму двух слагаемых.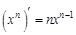 , где
, где 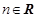
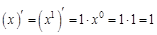
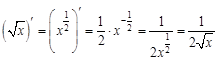

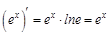
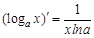

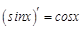

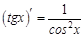
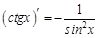



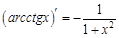
 .
.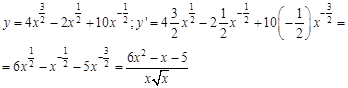

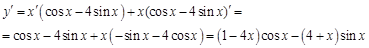

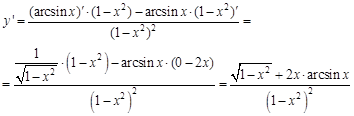
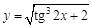
 встречается в выражении один раз). Если ввести обозначения вложенных функций, то получим следующее:
встречается в выражении один раз). Если ввести обозначения вложенных функций, то получим следующее: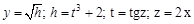
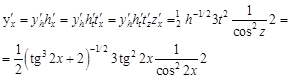

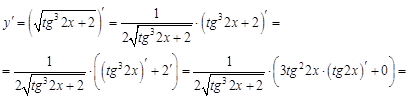
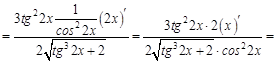
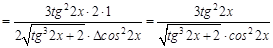
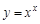
 . По правилам логарифмирования степень подлогарифмического выражения можно поставить перед логарифмом, тогда:
. По правилам логарифмирования степень подлогарифмического выражения можно поставить перед логарифмом, тогда: 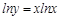 . Теперь можно искать производную. В ходе решения учтем, что
. Теперь можно искать производную. В ходе решения учтем, что 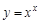 :
: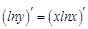
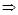
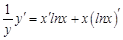
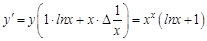
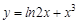
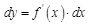
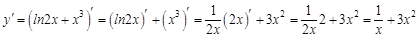
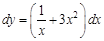
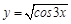
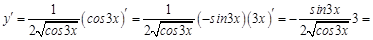
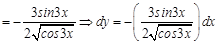
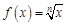 , где
, где 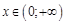 . Получить формулу для приблизительных вычислений значений данной функции и вычислить по ней значения
. Получить формулу для приблизительных вычислений значений данной функции и вычислить по ней значения 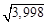 и
и 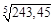 .
.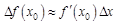 . Определим эту вид формулы для нашей функции. Для этого найдем производную функции
. Определим эту вид формулы для нашей функции. Для этого найдем производную функции 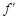 . Преобразуем в исходной формуле корень в степень и воспользуемся формулой для нахождения производной степенной функции:
. Преобразуем в исходной формуле корень в степень и воспользуемся формулой для нахождения производной степенной функции: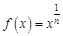 ;
;  , где
, где 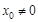 .
.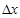 приращение функции в точке
приращение функции в точке  будет равно:
будет равно: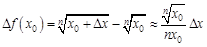 .
.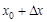 будет приблизительно равно:
будет приблизительно равно: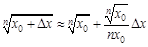 .
.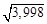 . Представим подкоренное выражение в виде суммы
. Представим подкоренное выражение в виде суммы 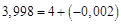 . Тогда:
. Тогда: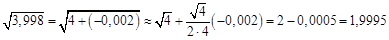
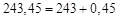 . Тогда:
. Тогда: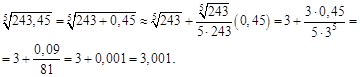
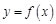 определена на некотором интервале (a, b), и пусть в каждой точке этого интервала она имеет производную
определена на некотором интервале (a, b), и пусть в каждой точке этого интервала она имеет производную 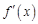 . Эту производную называют первой производной или производной первого порядка для данной функции. Эта производная сама может являться функцией
. Эту производную называют первой производной или производной первого порядка для данной функции. Эта производная сама может являться функцией 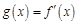 , определенной на интервале (a, b). Если функция
, определенной на интервале (a, b). Если функция 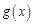 имеет на этом интервале производную в точке
имеет на этом интервале производную в точке 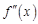 . Аналогично эта производная может являться функцией
. Аналогично эта производная может являться функцией 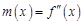 , определенной на интервале (a, b). Если и она имеет на интервале (a, b) в точке
, определенной на интервале (a, b). Если и она имеет на интервале (a, b) в точке 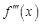 . Такие же рассуждения можно провести для производной любого порядка.
. Такие же рассуждения можно провести для производной любого порядка.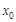 называют производную от производной (n-1)-го порядка в этой точке:
называют производную от производной (n-1)-го порядка в этой точке: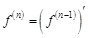 .
.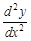 или
или 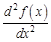 – производная второго порядка функции
– производная второго порядка функции 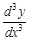 или
или 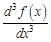 – третья производная функции
– третья производная функции 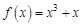 . Найдем все возможные производные высших порядков для этой функции.
. Найдем все возможные производные высших порядков для этой функции.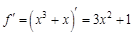
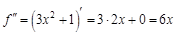
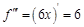
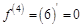
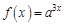 . Найдем 100-ю производную этой функции.
. Найдем 100-ю производную этой функции.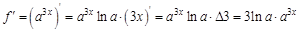
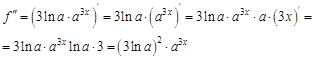
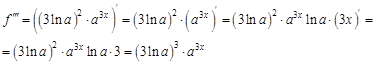
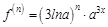 .
.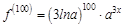 .
.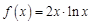 . Найдем несколько первых производных этой функции.
. Найдем несколько первых производных этой функции.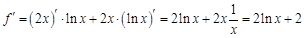
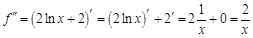
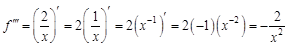
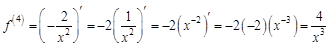
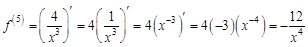
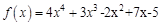
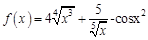
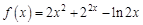
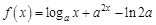
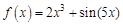
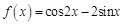
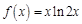
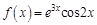
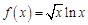
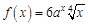
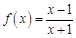
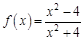
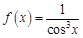
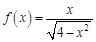
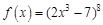
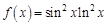
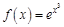
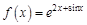
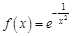
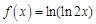
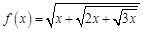
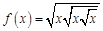
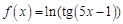
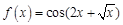
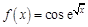
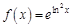
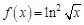
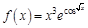
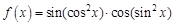
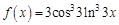
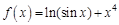
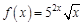
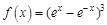
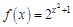
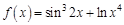
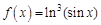
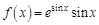
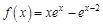
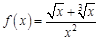
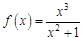
 в точке
в точке 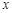 , если известно, что:
, если известно, что: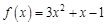 ,
,
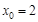 ,
,
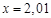
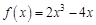 ,
,
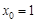 ,
,
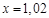
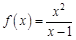 ,
,
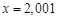
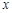 , если известно, что:
, если известно, что: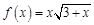 ,
,
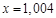
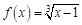 ,
,
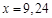
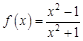 ,
,