
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розв ’ язок задачі методом перетворення Фур ’ є. ⇐ ПредыдущаяСтр 3 из 3
Рівняння Пуассона. Розв ’ язок задачі Діріхле в крузі методом Фур ’ є.
Питання до самоконтролю Вияснити фізичний зміст першої крайової задачі рівняння теплопровідності в однорідному стержні. Яка кількість теплоти протікає через поверхню S в просторі? Як називається вираз в дужках у рівнянні
В чому полягає задача Коші для випадку стержня, обмежаного з однієї сторони? Записати інтеграл імовірностей. Яку умову повинні задовільняти частинні розв ’ язки задачі Діріхле в крузі? Література: А.Н.Тихонов, А.А.Самаровский “Уравнения математической физики”, Гостехиздат, 1954. Н.С.Пискунов “Диференциальное и интегральное исчисление”, т.ч., Москва, 1972. П.И.Чинаев, Н.А.Минин и др. “Висшая математика, специальн ые главы ”, Киев, 1981. О.В.Мантуров та ін. “Математика в поняттях, означеннях, термінах”, т.ч., Київ, 1986. П.Е.Данко, А.Г.Попов “ Высшая математика в упражнениях и задачах ”, ч.2, Москва, 1974. Лекція №2.
Тема: Рівняння теплопровідності.
Розглянемо однорідний стержень довжини l. Будемо вважати, що бічна сторона стержня теплопроникна та що в усіх точках поперечного січення стержня температура однакова. Дослідимо процес розповсюдження тепла в стержні. Розмістимо вісь 0Х так, що один кінець стержня буде співпадати з точкою х=0, а другий – з точкою х=l (див. рис.). Нехай u(x,t) – температура в січній стержня з абсцисой х в момент t. Дослідним шляхом визначимо, що швидкість розповсюдження тепла пролягаючого через січну з абсцисой х за одиницю часу, визначається формулою
розглянем елемент стержня, заключений між січними з абсцисами х1 і х2 (х2-х1=Dх). Кількість тепла, що пройшло через січну з абсцисою х1 за час Dt, буде рівно
те ж саме для січної з абсцисою х2
Прилив тепла DQ1-DQ2 в елемент стержня за час Dt буде рівний:
(Ми використали теорему Лагранжа до рівності Цей прилив тепла за час Dt пішов на підвищення температури елемента стержня на величину DU:
DQ1-DQ2=cqDxSDU
де с – теплоємність речовини стержня, q – щільність речовини стержня (qDxS – маса елемента стержня). Прирівнюючи вирази (4) і (5) одної і тої ж кількості тепла DQ1-DQ2, вийде:
або
Позначаючи k/cq=a2, ми одержуєм:
Це і є рівняння теплопровідності в однорідному стержні. Щоб рішення рівняння (6) було повністю визначено, функція u(x,t) має задовільняти крайові умови. Крайові умови для рішення рівняння (6) можуть бути різні. Умови, які відповідають так званій першій крайовій задачі для 0£t£T, слідуючі: u(x,t)=j(x) (7) u(x,t)=y1(t) (8) u(x,t)=y2(t) (9) Фізичні умови (7) (початкові умови) відповідають тому, що при t=0 в різних січних стержня задана температура, рівна j(х). Умови (8) і (9) (граничні умови) відповідають тому, що на кінцях стержня при х=0 і при х=l підтримується температура, рівна y1(t) і y2(t) відповідно.
Тема: Розв ’ язок задачі методом перетворення Фур ’ є. Нехай в початковий момент задана температура в різних січних необмежаного стержня. Потрібно визначити розподіл температури в стержні в наступні моменти часу. Якщо стержень співпадає з віссю 0Х, то математично задача формулюється слідуючим образом. Знайти рішення рівняння
в області -¥<x<¥, t>0, задовільняюче початковій умові u(x,0)=j(x) (2) будемо шукати частинне рішення рівняння (1) у вигляді добутку двух функцій: u(x,0)=-X(X)T(t). (3) Підставляючи в рівняння (1), будем мати: X(x)T¢(t)=a2X¢¢(x)T(t) або
Кожне з цих відношень не може залежати ні від х, ні від t, і тому ми їх прирівняємо постійній -l2. З формули (4) отримаємо два рівняння:
T¢+a2l2T=0, (5) X¢¢+l2X=0. (6) Рішаючи їх знайдем:
Підставляючи в (3), отримаємо:
постійна С включається в А(l) і В(l). Для кожного значення l ми торимаєм рішення виду (7). Произвольн ы е постійні А і В для кожного значення l мають визначені значення. Виходячі з цього можна рахувати А і В функціями від l. Сума рішень виду (7) також є рішенням:
Інтегруючи вираз (7) по параметру l в границях від 0 до ¥ також отримаємо рішення
якщо А(l) і В(l) такі, що цей інтеграл, його похідна по t і друга похідна по х існують і дістаютьсяшляхом диференціювання інтеграла по t і по х. Підберем А(l) і В(l) так, щоб рішення u(x,t) задовільняло умові (2). Покладаючись в рівності (8) t=0, на основі умови (2) дістанемо:
Припустимо, що функція j(х) такова, що вона представіма інтегралом Фур’є:
або
зрівнюючи праві частини (9) і (10), отримаємо:
підставляючи знайдені вирази А(l) і В(l) у формулу (8) отримаємо:
або, міняючи порядок інтегрування, отримаємо
Це і є рішення поставленої задачі. Перетворемо формулу (12). Обрахуємо інтеграл, що стоїть в круглих душках:
Це перетворення інтеграла зроблено шляхом підстановки
Позначимо
Диференціюючи, отримаємо:
Інтегруючи по частинах, знайдем:
або
Інтегруючи це диференціальне рівняння, отримаєм:
Знайдем постійну С. З (15) слідує:
Отже, в рівності (16) має бути
Тоді,
Значення (17) інтеграла (15) підставляємо у (13)
Підставляючи замість b його вираз (14), отримаємо кінцеве значення інтеграла (13):
Підставивши цей вираз інтеграла у рішення (12), отримаємо:
Ця формула, інтеграл Пуассона, представляє собою рішення поставленої задачі. Встановимо фізичний зміст формули (19). Розглянемо функцію 0 при -¥<x<x0, j*(х)= j(x) при x0£x£x0+Dx, (20) 0 при x0+Dx<x<¥. Тоді функція
є рішенням рівняння (1), що приймає при t=0 значення j*(х). Приймаючи до уваги (20), ми можемо записати:
Примінем теорему про середнє до останього інтегралу, отримаємо:
Формула (22) дає значення температури в точці стержня в довільний момент часу, якщо при t=0 в усьому стержні температура u*=0, крім відрізка [x0,x0+Dx], де вона рівна j(х). Сума температур виду (22) і дає рішення (19). Замітимо, що якщо r - лінійна густина стержня, с – темплоємність матеріала, то кількість тепла в елементі [x0,x0+Dx] при t=0 буде DQ»j(x)Dxrc. (23) Розглянемо далі функцію
зрівнюючи її з правою частиною формули (22) з урахуванням (23), говорять, що вона дає значення температур в любій точці стержня в довільний момент часу t, якщо при t=0 в січній x було миттєве джерело теплоти з кількістю тепла Q=cr.
Тема: Рішення задачі Діріхле для кола.
Нехай в площині 0ху є коло радіусом R з центром на початку координат і на його окружності задана деяка функція f(j), де j - полярний кут. Потрібно знайти функцію u(r,j), непреривну в колі, включаючи границю, задовільняючу всередині кола рівнянню Лапласа
і на окружності кола що приймає задані значення
Будем рішати задачу в полярних координатах. Перепишемо рівняння (1) в цих координатах:
Будем шукати рішення методом розділення змінних, покладаючи U=Ф(j)R(r). (3) Підставляючи в ріність (1’), вийде: r2Ф(j)R¢¢(r)+rФ(j)R¢(r)+Ф¢¢(j)R(r)=0 або
Так як ліва частина цієї рівності не залежить від r, а права від j, отже, вони рівні постійному числу, яке ми позначаємо через –k2. Таким чином рівність (4) дає нам два рівняння: Ф¢¢(j)+k2Ф(j)=0, (5) r2R¢¢(r)+rR¢(r)-k2R(r)=0 (5¢) Загальне рішення рівності (5) буде Ф=Аcoskj+Bsinkj. (6) Рішення рівняння (5¢) будем шукати у формі R(r)=rm. Підставляючи R(r)=rm у (5¢), дістанемо: r2m(m-1)rm-1-k2rm=0 або m2-k2=0. Отже, маємо два лінійно незалежних рішення rk і r-k. Загальне рішення рівняння (5¢) буде R=Crk+Dr-k. (7) Вираз (6) і (7) підставляємо у (3): Uk=(Akcoskj+Bksinkj)(Ckrk+Dkr-k). (8) Функція (8) буде рішенням рівняння (1¢) при довільному значенні k, відмінним від 0. Якщо k=0, то рівняння (5) і (5¢) приймають вид: Ф¢¢=0, rR(r)+R¢(r)=0, отже, U0=(A0+B0j)(C0+D0lnr). (8¢) Рішення має бути періодичною функцією від j, так як при одному і тому ж значенні r при j і j+2p ми маємо мати одне і те ж значення рішення, тому що розглядається одна і та ж точка кола. Виходячі з цього очевидно, що у формулі (8¢) має бути В0=0. Далі, ми шукаємо рішення, непреривне і кінцеве в колі. Отже, в центрі кола при r=0 рішення має бути кінцевим, і тому у формулі (8¢) має бути D0=0, а у формулі (8) Dk=0. Таким чином, права частина (8¢) перетворюється в добуток А0С0, яке ми позначимо як А0/2. Отже,
Ми будем складати рішення нашої задачі у вигляді суми рішень виду (8), так як сума рішень є рішення. Сума має бути періодичною функцією від j. Для цього k має приймати цілі значення. Ми маємо обмежитись тільки додатніми значеннями K=1, 2, …, n, …, так як в силу произвольности постійних А, В, С, D від’ємні значення k нових частинних рішень не дають. Отже,
(постійна Сn включена у An i Bn). Тепер підберемо произвольн ы е постійні An і Bn так, щоб задовільнялась крайова умова (2). Підставляючи в рівність (9) r=R, на основі умови (2) дістанемо:
Щоб мала місце рівність (10), потрібно, щоб функція f(j) розкладалась в ряд Фур’є в інтервалі (-p,p), та щоб AnRn і BnRn були її коефіцієнтами Фур’є. Отже, An і Bn мали визначатись по формулам:
Отже, ряд (9) з коефіцієнтами, визначиними по формулам (11), буде рішенням нашої задачі, якщо допускає почленне двухкратне диференціювання по r і j. Перетворемо формулу (9). Підставляючи замість An і Bn їх вирази (11) і виконуючі тригонометричні перетворення, дістанем:
Перетворимо вираз, що стоїть в квадратних душках:
Замінюючи вираз, що в квадратних душкаху у формулі (12), виразом (13), отримаюмо:
Формула (14) називається інтегралом Пуассона. Шляхом аналізу цієї формули доводиться, що якщо формула f(j) неперервна, то функція U(r,j), визначена інтегралом (14), задовільняє рівність (1¢) і при r®R буде U(r,j)®f(j), тобто U(r,j) являє собою рішення поставленої задачі Діріхле для кола.
|
|||||||||||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 123; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.151.153 (0.059 с.) |
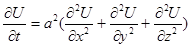 Що це за рівняння?
Що це за рівняння?
 (1)
(1) (2)
(2) (3)
(3) (4)
(4) ).
). (5)
(5)
 .
. (6)
(6) (1)
(1) . (4)
. (4)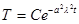 , X=Acoslx+Bsinlx.
, X=Acoslx+Bsinlx.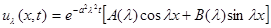 (7)
(7) .
.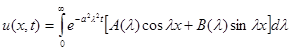 , (8)
, (8)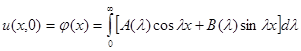 . (9)
. (9)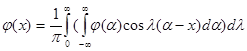
 . (10)
. (10) (11)
(11)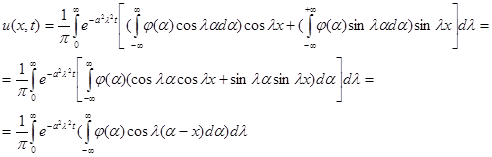
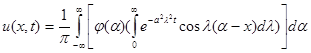 . (12)
. (12)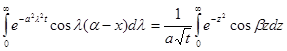 . (13)
. (13) . (14)
. (14) . (15)
. (15)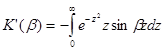 .
.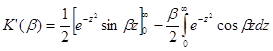

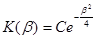 . (16)
. (16)
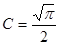 .
. . (17)
. (17) .
. . (18)
. (18)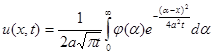 . (19)
. (19) (21)
(21) .
.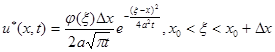 . (22)
. (22) . (24)
. (24) . (1)
. (1) . (2)
. (2) (1¢)
(1¢) . (4)
. (4)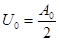 . (8¢¢)
. (8¢¢)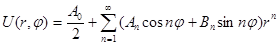 (9)
(9)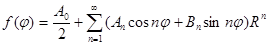 . (10)
. (10) . (11)
. (11)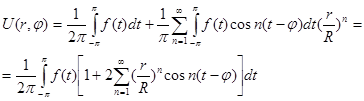 . (12)
. (12) . (13)
. (13)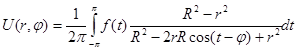 . (14)
. (14)


