Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклади постановок таких задач.
Класифікація диференціальних рівнянь 2-го порядку в частинних похідних. Рівняння коливань струни. Розв ’ язок задачі Коші методом Даламбера Питання для самоконтролю. Лекція №1. В чому полягає дисципліна: рівняння математичної фізики? Від чого залежить розв ’ язування рівнянь з частинними похідними 2-го порядку? Приклади рівнянь еліптичного типу. 4. Як називається і до якого типу належить рівняння:
В чому полягає крайова задача для рівняння коливання струни? Записати формулу Даламбера, яка дає розв ’ язок одномірного однорідного хвильового рівняння. Література: А.Н.Тихонов, А.А.Самаровский “Уравнения математической физики”, Гостехиздат, 1954. Н.С.Пискунов “Диференциальное и интегральное исчисление”, т.ч., Москва, 1972. П.И.Чинаев, Н.А.Минин и др. “Висшая математика, специальн ые главы ”, Киев, 1981. О.В.Мантуров та ін. “Математика в поняттях, означеннях, термінах”, т.ч., Київ, 1986. П.Е.Данко, А.Г.Попов “ Высшая математика в упражнениях и задачах ”, ч.2, Москва, 1974. Лекція №1. Тема: Основні задачі математичної фізики.
В курсі вищої математики вивчалися звичайні диференціальні рівняння, розв’язками яких є функції відносно аргументу. Але багато задач в математиці, фізиці, електроніці, радіотехніці та в інших науках приводять до диференціальних рівняннь відносно функцій двох, трьох та більше числа аргументів – диференціальні рівняння в частинних похідних. Існує спеціальна дисципліна, яка полягає в математичному опису явищ, пов’язаних з деякими фізичними процесами, що описуються за допомогою рівняннь у частинних похідних і (рідко) за допомогою інтегральних рівняннь або інтегро-диференціальних рівняннь. Ця математична диспліна називається рівняннями математичної фізики. Провідне місце в рівняннях математичної фізики посідає теорія рівняннь з частинними похідними 2-го порядку:
де аij, bi, c – задані функції змінних х1, х2, …, х3 (n ³2). Властивості розв’язування цих рівняннь істотно залежать від знаків коренів характеристичного рівняння det(|| alk|| - lE)=0. Так для диференціального рівняння з частинними похідними 2-го порядку характеристичне рівняння буде:
d11dy2-2a12dxdy+a22dx2=0. Інтеграли цього рівняння називаються характеристиками. Це характеристичне рівняння можна записати й так
Якщо а12-а11а22>0, то інтеграли характеристичного рівняння j(х,у)=С1 і y(х,у)=С2 дійсні і різні. В цьому випадку кажуть, що рівняння має гіперболічний тип. Якщо І якщо До рівнянь гіперболічного типу приводять задачі про коливання суцільних середовищ і задачі про електромагнітні коливання: процеси поперечних коливань струни, поздовжніх коливань стержня, електричних коливань в проводі, крутильних коливаннь валу, коливань газу і т. д. Найпростішим з них є хвильове рівняння Рівняння параболічного типу дістають при дослідженні таких фізичних явищ, як теплопровідність, дифузія, поширення електромагнітних хвиль у провідних середовищах, рух в’язкої рідини, деякі питання теорії імовірностей і т. д. Найпростішим з них є рівняння теплопровідності, або рівнянням Фур’є:
До рівняннь еліптичного типу приводить вивчення різних стаціонарних процесів (електростатика, магнітостатика, потенціальний рух рідини, що не стискується, тощо). Найпростішими з них є рівняння DU=0 (Лапласа); DU=C (Пуассона), а також рівняння, яке розглядав Ейлер: DU+kU=0, і полігармонійні рівняння. В кожному з цих типів рівняннь шукана функція U залежить від двох змінних. Розглядаються також відповідні рівняння і для функції з більшими числом змінних. Так хвильове рівняння з трьома незалежними змінними має вид:
рівняння теплопровідності з трьома незалежними змінними має вид:
рівняння Лапласа з трьома незалежними змінними має вид:
Тема: Рівняння коливань струни.
В математичній фізиці під струною розуміють гнучку ніть. Напруги, що з’явились в струні в любий момент часу, напрямлені по дотичній до її профелів. Нехай струна довжини l в початковий момент напрямлена по відрізку осі 0Х від 0 до l. Припустимо, що кінці струни закріплені в точках Х=0 і Х=l. Якщо струну відхилити від її початкового положення, а потім предоставить самій собі або, не відхиляючи струни, придати в початковий момент її точкам деяку швидкість, або відхилити струну і придати її точкам деяку швидкість, то точки струни будуть виконувати рух – говорять, що струна починає коливатись. Задача заключається у ввизначенні форми струни в любий момент часу і у визначенні закону руху кожної точки струни в залежності від часу.
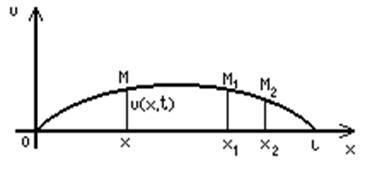
Розглянемо малі відхилення точок струни від початкового положення. В силу цього можна припускати, що рух точок струни проходить перпендикулярно осі 0Х і в одній площі. При цьому препущенні процес коливань струни описується однією функцією u(x,t), яка дає величину переміщення точки струни з абсцисой х в момент t (рис.1).
Так як ми розглядаємо малі відхилення струни в площі (x,u), то будемо припускати, що довжина елемента струни ¾М1М2 рівна її проекції на вісь 0Х, ¾М1М2=х2-х1. Також будем припускати, що натяг в усіх точках струни однаковий; позначимо його як Т.
Розглянемо елемент струни ММ' (рис 2). На кінцях цього елемента, по дотичним до струни, діють сили Т. нехай дотичні створять з віссю 0Х кути j та j+Dj. тоді проекція на вісь 0u сил, діючих на елемент ММ', буде рівна Тsin(j+Dj)-Tsinj. Так як кут j малий, то можна покласти tgj=sinj, і ми отримаємо:
(тут ми примінили теорему Лагранжа до виразу, що стоїть у квадратних душках). Щоб получити рівняння руху, потрібно зовнішні сили прирівняти силі інерції. Нехай r - лінійна щільність струни. Тоді маса елемента струни буде rDх. Прискорення елемента дорівнює
Скорочуючи на Dх і позначаючи Це і є хвильове рівняння – рівняння коливань струни. Для повного визначення руху струни одного рівняння (1) недостатньо. Шукана функція u(x,t) повинна ще задовільнятись граничним умовам, вказуючим, що робиться на кінцях струни (х=0 і х=1), та початковим умовам, описуючим стан струни в початковий момент (t=0). Суцільність граничних та початкових умов називається краєвими умовами. Нехай, наприклад, як ми припускали, кінці струни при х=0 і х=1 нерухомі. Тоді при довільному t мають виконуватись рівності: u(0,t)=0, u(l,t)=0. Ці рівності є граничними умовами для нашої задачі. В початковий момент t=0 струна має визначену форму, яку ми їй надали. Нехай ця форма визначається функцією f(x). Таким чином, має бути
Далі, в початковий момент має бути задана швидкість в кожній точці струни, яка визначається функцією j(х).Таким чином, має бути
Умови (2) і (3) являються початковими умовами.
Тема: Розв ’ язок задачі Коші методом Даламбера. Розглянемо ще один метод рішення хвильового рівняння – метод Даламбера. Візьмем випадок, коли граничні умови нас не цікавлять або коли їх можна не враховувати. В цих випадках задача ставиться так: Знайти рішення хвильового рівняння Utt-a2uxx=0 (t=y, a11=-a2, a12=0, a22=1), Задовільняюче початковим умовам U(x,0)=j(x); ut(x,0)=y(x) де j(х) і y(x) – задані у Зведем хвильове рівняння до канонічного виду, що містить змішану похідну. Тут характеристичне рівняння
A11dt2-2a12dxdt+a22dx2=0 Прийме вид -a2dt2+dx2=0, або dx2-a2dt2=0. Воно розпадається на два рівняння: dx-adt=0 і dx+adt=0 інтеграли яких будуть x-at=C1, x+at=C2 введемо нові змінні x=x-at, h=x+at. Тоді xх=1, xt=-a, hx=1, ht=a, ux=uxxx+uhhx=ux+uh, uxx=uxxxx+uxhhx+uhxxx+uhhhx=uxx+2uxh+uhh, ut=uxxt+uhht=-aux+auh, utt=-auxxxt-auxhht+auhxxt+auhhht=a2uxx-2a2uxh+a2uhh. Підставивши uxx, utt в вихідне рівняння, отримаємо a2uxx-2a2uxh+a2uhh-a2(uxx+2uxh+uhh)=0, -4a2uxh=0, uxh=0. Отримане рівняння можна записати як:
Звідси випливає, що uh не залежить від x: uh=f*(h), де f*(h) – довільна функція h. Інтегруючи останню рівність по h при фіксованому x, маємо
де f1(x) і f2(h) – довільні двічі диференціюючі функції аргументів x і h. Враховуючи, що x=х-at і h=x+at, дістаєм загальне рішення даного рівняння у вигляді u(x,t)=f1(x-at)+f2(x+at). Визначимо функції f1 і f2 так, щоб функція u(x,t) задовільняла початковим умовам: u(x,t)=f1(x)+f2(x)=j(x), ut(x,0)=-af¢1(x)+af¢2(x)=y(x). Таким чином, для знаходження функцій f1 і f2 маємо систему рівнянь f1(x)+f2(x)=j(x), -af¢1(x)+af¢2(x)=y(x). Інтегруючи другу рівність, отримаємо
де х0 і С – постійні. Тоді f1(x)+f2(x)=j(x),
Звідси знаходимо
і
Підставивши у вираз для u(x,t) знайдені значення f1 і f2, отримаємо
Ця рівність називається формулою Даламбера. Раніше функцію u(x,t) ми записували як: u(x,t)=f1(x-at)+f2(x+at), де перший додаток
при x-at=const зберігається постійне значення. Отже, функція f1(x-at) описує розповсюдження прямої бігучої хвилі без викревлення. Аналогічно функція
являє собою обратну біжучу хвилю без викревлень, щорозповсюджуються з тією ж швидкістю, але в від¢ємному напрямку вісі 0Х. В цілому процес розповсюдження коливань, функції u(x,t), представляє собою суперпозицію (накладання) прямої та оберненої біжучих хвиль без викревлень.
Лекція №2 План
Рівняння теплопровідності.
|
|||||||||||||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 201; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.56.45 (0.049 с.) |
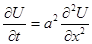 ?
?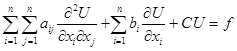

 , то характеристичне рівняння має комплексні (спряжені) загальні інтеграли і є рівнянням еліптичного типу.
, то характеристичне рівняння має комплексні (спряжені) загальні інтеграли і є рівнянням еліптичного типу.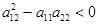 , то характеристичне рівняння має комплексні (спряжені) загальні інтеграли і є рівнянням еліптичного типу.
, то характеристичне рівняння має комплексні (спряжені) загальні інтеграли і є рівнянням еліптичного типу. , відкрите Ейлером у 1759році.
, відкрите Ейлером у 1759році.




 . Отже, по принципу Даламбера будем мати:
. Отже, по принципу Даламбера будем мати: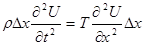
 , получаємо рівняння руху
, получаємо рівняння руху 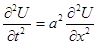 . (1)
. (1)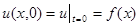 . (2)
. (2)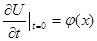 . (3)
. (3)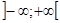 функції.
функції.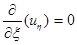 .
. .
.
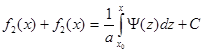 .
. ,
, .
. ,
, .
.