
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование следящей системы
Цельработы: освоить различные способы описания линейных динамических систем и методы их моделирования в пакетах MATLAB и SIMULINK.
1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ 1.1. Описание систем структурной схемой и передаточной функцией. В инженерной практике используются различные способы задания динамических систем – с помощью структурных схем, передаточных функций, дифференциальных уравнений, а также с помощью частотных и временных характеристик. Проиллюстрируем их на примере следящей системы, структурная схема которой представлена на рис.1. В ее состав входят инерционное усилительное звено с передаточной функцией k / (T 1 p + 1 ), двигатель с передаточной функцией 1 / (T 2 p) и вычитающее устройство для сравнения входного сигнала u и выходного сигнала следящей системы y. Следящая система должна работать таким образом, чтобы угол поворота двигателя у по возможности точно равнялся значению входного сигнала и (задача слежения).
Способ задания моделей объектов с помощью схемы (типа приведенной на рис.1) называется структурным, поскольку он отражает реальную структуру объекта. По передаточным функциям отдельных блоков можно построить общую передаточную функцию следящей системы Для этого в соответствии со структурной схемой выписывается система уравнений
которая затем преобразуется к одному уравнению, путем исключения переменной e (p):
Далее, выражая выходной сигнал Y (p) через входной U (p), получаем
где Q (p) - передаточная функция системы. В нашем случае она имеет вид
По сравнению со структурным описанием передаточная функция является более компактной математической моделью, в то же время она позволяет анализировать такие характеристики, как устойчивость и минимальность объекта.
1.2. Описание систем дифференциальными уравнениями. От передаточной функции легко осуществить переход к описанию системы с помощью дифференциального уравнения. В рассматриваемом случае для этого достаточно в уравнении
раскрыть скобки и заменить оператор p оператором дифференцирования d / d t
Решая это дифференциальное уравнение, можно найти реакцию следящей системы на любое входное воздействие. Аналитическое решение y (t) дифференциального уравнения (2) является суммой решения однородного уравнения y одн(t) и частного решения дифференциального уравнения yчастн(t). Для получения y одн (t) составляем характеристическое уравнение T 1 T 2 p 2 + T 2 p + k = 0. и находим его корни p 1 и p 2. Если они вещественные и различные, то решение однородного уравнения ищется в виде Во всех случаях система оказывается устойчивой, если корни лежат в левой полуплоскости (при этом решение однородного уравнения с течением времени стремится к нулю). Частное решение дифференциального уравнения определяется видом правой части дифференциального уравнения (2). Если, например, там стоит экспоненциальная функция u = e - t, то и частное решение нужно искать в виде экспоненты yчастн = Ce - t. Если u = 1 (t), его следует искать в виде константы yчастн = C. Для определения C надо подставить частное решение в дифференциальное уравнение. Учитывая, что производная от константы равна нулю, находим, что в последнем случае C = 1. Значения постоянных С 1, С 2 определяются путем подстановки в полученное решение начальных условий. Например, в случае нулевых начальных условий и решения вида
C 1 + C 2 + 1 = 0; p 1 C 1 + p 2 C 2 = 0.
Пример 1: Дано дифференциальное уравнение:
Решая это дифференциальное уравнение, можно найти реакцию следящей системы на любое входное воздействие. Так как Найдем общее решение дифференциального уравнения по его характеристическому полиному
Найдем частное решение дифференциального уравнения по виду правой части Подставив его в исходное уравнение получим Решением дифференциального уравнения будет следующее выражение:
Найдем первую производную, используя информацию о производных от элементарных функций в приложении:
После преобразования и решения получим С1=0.12, С2=-1.5. В соответствии с этим решением дифференциального уравнения будет следующее выражение:
Наряду с заданием объекта одним дифференциальным уравнением типа (2) часто используют описание с помощью системы дифференциальных уравнений первого порядка. Оно известно как матричное описание или описание в пространстве состояний. Для получения описания следящей системы в пространстве состояний выберем в качестве переменных состояния x 1 и x 2 выходные сигналы звеньев первого порядка на структурной схеме рис. 1. Составим для каждого из них дифференциальное уравнение первого порядка
Кроме того, запишем алгебраическое уравнение для выходного сигнала y = x2. В матричном виде это описание имеет вид
где
Анализируя это описание, можно оценить устойчивость, управляемость, наблюдаемость и другие характеристики системы.
1.3. Взаимосвязь описаний. Все рассматриваемые виды описаний тесно взаимосвязаны, поэтому, зная одно из них, можно получить остальные. Например, связь между матрицами A, b, c описания в пространстве состояний и передаточной функцией системы Q(p) задается уравнением
где p - оператор Лапласа, E - единичная матрица. Любое из рассмотренных описаний системы позволяет рассчитывать ее реакцию на типовые входные сигналы. Чаще всего систему характеризуют реакцией на дельта-функцию u = d (t) и на единичную функцию (функцию единичного скачка) u = 1 (t). Эти реакции известны как импульсная весоваяхарактеристика системы y = q (t) и переходная характеристика y = p (t). Их изображения по Лапласу связаны с передаточной функцией формулами
которые удобно использовать для нахождения весовой и переходной характеристики. Другой подход к описанию системы связан с использованием частотных характеристик. Они получаются рассмотрением функции комплексной переменной, получаемой из формулы (3) заменой p = j w: Q (j w) = c(j wE – A) – 1 b.
1.4. Моделирование в пакете MATLAB и SIMULINK. Пакет MATLAB поддерживает все виды описаний динамических систем, включая структурные схемы, передаточные функции и матричное описание в пространстве состояний. Для работы со структурными схемами в пакете MATLAB имеется приложение SIMULINK. Его можно вызвать, набирая в командном окне MATLAB команду simulink. Численное моделирование следящей системы в MATLAB выполняется с помощью команд impulse, step, lsim. Предварительно надо ввести числитель num и знаменатель den передаточной функции либо матрицы A, B, C, D описания в пространстве состояний и сформировать структуру sys=tf(num,den) либо sys=ss(A,B,C,D). После этого весовая функция и переходная функция находятся командами impulse(sys), step(sys), а реакции на произвольные входные сигналы, такие как u = e - t, рассчитываются с помощью команды lsim. Реализация различных соединений блоков может быть осуществлена программно с помощью команд parallel, series, feedback, append и некоторых других. Для этой цели можно использовать также команды +, –, *.
В MATLAB можно получать не только численное, но и символьное решение дифференциальных уравнений. Это делается с помощью команды dsolve тулбокса SYMBOLIC. Входными аргументами команды служат дифференциальное уравнение и начальные условия. Например, для решения дифференциального уравнения >> y=dsolve('D2у+3*Dу+2*y=2', 'Dy(0)=0','y(0)=0') MATLAB выдаст ответ y =1+exp(-2*t)-2*exp(-t), т.е. y= 1+ e –2 t –2 e–t. 2. ЗАДАНИЕ ПО РАБОТЕ И СОДЕРЖАНИЕ ОТЧЕТА
В работе исследуется динамика следящей системы, заданной структурной схемой (рис.1) при значениях параметров k, T 1, T 2, приведенных в таблице вариантов заданий. Отчет по работе должен содержать: 1. Исходную схему моделирования с заданными численными значениями параметров и передаточную функцию Q (p), полученную из уравнения (1). 2. Дифференциальное уравнение второго порядка, описывающее следящую систему, его аналитическое решение и график выходного сигнала y (t) при входном сигнале 3. Описание следящей системы в пространстве состояний, передаточную функцию системы, полученную по формуле (3). Формулы и графики весовой и переходной характеристик. 4. Схемы моделирования следящей системы применительно к SIMULINK, содержащие осциллографы и генераторы входных сигналов (для генерирования сигнала u = e – t использовать интегратор с обратной связью). Программы численного и символьного моделирования в MATLAB.
3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. С помощью пакета SIMULINK построить схему моделирования в соответствии с рис. 1. Получить графики выходных сигналов (весовой функции, переходной функции и реакции на u = e – t). Проверить их соответствие расчетным. 2. Параллельно со схемой моделирования следящей системы набрать модель передаточной функции Q (p) следящей системы и сравнить их выходные сигналы. 3. Выполнить моделирование в пакете MATLAB, используя разные описания системы. Сравнить результаты моделирования в MATLAB и SIMULINK. 4. Построить графики фазовых траекторий в плоскости (x 1, x 2) (в SIMULINK для этого потребуется блок XY-graph). Построить частотные характеристики следящей системы, используя команды bode, nyquist, ltiview.
4. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Описать общую процедуру перехода от произвольной структурной схемы к системе линейных дифференциальных уравнений первого порядка. 2. Найти реакцию своего варианта следящей системы на входной сигнал
3. Найти передаточную функцию следящей системы, если устройство сравнения реализовано в соответствии с одной из следующих формул:
4. Как повлияет изменение знака обратной связи в следящей системе на ее устойчивость и вид переходной характеристики? 5. Найти передаточную функцию следящей системы, если передаточная функция двигателя равна
5. Найти матрицы описания в пространстве состояния для пп.3 и 5. 6. Сравнить графики весовой и переходной функций разомкнутой и замкнутой системы для своего варианта заданий.
5. ВАРИАНТЫ ЗАДАНИЙ
Практическая работа № 4
АНАЛИЗ СИСТЕМЫ УПРАВЛЕНИЯ
Цель работы: исследовать теоретически и с помощью пакета MATLAB устойчивость, управляемость, наблюдаемость и минимальность системы управления, заданной структурной схемой, и построить ее модель пониженного порядка.
1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
1.1 Анализ устойчивости. Понятие устойчивости является одним из основных в теории управления. Устойчивой называют систему, которая, будучи выведена из состояния равновесия, стремится вновь вернуться в это состояние. Для неустойчивых систем характерна обратная тенденция. Примером неустойчивой системы может быть карандаш, стоящий на острие. Обычно исследование устойчивости систем сводится к анализу устойчивости соответствующих дифференциальных уравнений. У неустойчивых уравнений решение неограниченно возрастает со временем. В теории автоматического управления существуют различные методы анализа устойчивости. Для линейных систем разработаны критерии устойчивости, которые можно разделить на корневые, алгебраические и частотные. Корневойкритерий устойчивости. Для того чтобы линейная динамическая система была устойчивой, необходимо и достаточно, чтобы все корни ее характеристического уравнения лежали в левой комплексной полуплоскости. Например, математическая модель системы, описываемой дифференциальным уравнением
устойчива, так как корни характеристического уравнения р 2+2 р +5=0 имеют отрицательные вещественные части p 1,2= –1±2 i, т.е. лежат слева от оси ординат. Алгебраический критерий устойчивости. Алгебраические критерии устойчивости позволяют судить об устойчивости на основе анализа коэффициентов характеристического полинома. Наибольшую известность получил критерий устойчивости Гурвица. Из него, в частности, следует, что все коэффициенты устойчивого дифференциального уравнения должны быть положительны. Для уравнений второго порядка это необходимое и достаточное условие. Для уравнений третьего порядка
помимо положительности коэффициентов, должно выполняться дополнительное условие, а именно, произведение средних коэффициентов должно быть больше произведения крайних: а 2 а 1> а 0 а 3. Например, уравнение
Частотный критерий устойчивости. Частотные критерии носят графический характер. Они опираются на анализ графиков частотных характеристик – АЧХ, ФЧХ, АФХ (последняя известна также как диаграмма Найквиста). Часть из них позволяет делать заключение об устойчивости замкнутой системы управления по частотным характеристикам разомкнутой системы. Приведем в качестве примера критерий Найквиста. Обозначим передаточную функцию разомкнутой системы Q(p) и охватим ее единичной отрицательной обратной связью (рис. 1).
Пусть известно, что разомкнутая система устойчива. Тогда для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф Найквиста разомкнутой системы не охватывал точку с координатами (-1, 0 j) на комплексной плоскости. В тулбоксе CONTROL пакета MATLAB диаграмма Найквиста системы sys строится командой nyquist(sys), указанная точка помечена на ней красным крестиком. В лабораторной работе исследуется система управления, заданная структурной схемой, поэтому для анализа устойчивости надо сначала найти ее передаточную функцию. Структурная схема исследуемой системы приведена на рис. 2. В ее состав входят три апериодических звена, а также суммирующие и вычитающие звенья. В схеме можно указать три пути от входа до выхода с передаточными функциями
Рис. 2. Структура исследуемой системы
Общая передаточная функция получается, как их сумма
Здесь A(p) и B(p) – некоторые полиномы от p (свои для каждого варианта). Характеристический полином системы равен знаменателю этой передаточной функции
На основе приведенных выше критериев устойчивости можно заключить, что если коэффициенты T 1, T 2, T 3 положительны, то система будет устойчивой. Анализ устойчивости замкнутой системы можно осуществить с помощью критерия Найквиста.
1.2. Анализ управляемости и наблюдаемости. Понятия управляемости и наблюдаемости широко используются в современной теории автоматического управления. Линейная система называется управляемой, если с помощью входного сигнала ее можно перевести из начала координат в любую точку пространства состояний. Система называется наблюдаемой, если по измерениям входного и выходного сигналов можно однозначно определить ее начальное состояние. Анализ управляемости и наблюдаемости выполняется с помощью матриц управляемости и наблюдаемости или с помощью грамианов управляемости и наблюдаемости. Те и другие строятся по описанию в пространстве состояний
Чтобы получить такое описание, воспользуемся структурной схемой, приведенной на рис. 2. Выпишем операторные уравнения для каждого блока схемы
и преобразуем их к виду
Выполняя обратное преобразование Лапласа, получаем систему линейных дифференциальных уравнений первого порядка
Кроме того, имеем алгебраическое уравнение для выходного сигнала y= x 1– x 3. Переписывая эти уравнения в матричной форме (3), получаем следующие выражения для матриц A, b, c:
где ненулевые элементы матриц имеют вид
Теперь можно перейти к анализу управляемости и наблюдаемости. Сформируем на основе матриц A, b, c две вспомогательные матрицы
Матрицы R и D называются соответственно матрицей управляемости и матрицей наблюдаемости системы. В пакете MATLAB их можно построить с помощью команд ctrb и obsv. К ритерийуправляемости. Для того чтобы система (3) была управляемой, необходимо и достаточно, чтобы матрица управляемости имела полный ранг rankR = n. К ритерийнаблюдаемости. Для того чтобы система (3) была наблюдаемой, необходимо и достаточно, чтобы матрица наблюдаемости имела полный ранг rankD = n. В случае систем с одним входом и одним выходом матрицы R и D квадратные, поэтому для проверки управляемости и наблюдаемости достаточно вычислить определители матриц R и D. Если они не равны нулю, то матрицы имеют полный ранг. Другой способ проверки управляемости и наблюдаемости опирается на вычисление грамианов управляемости и наблюдаемости. Так называются симметричные квадратные матрицы Wc и Wo, определяемые равенствами
В пакете MATLAB их можно найти с помощью команд типа gram(sys, ‘c’), gram(sys, ‘o’). Необходимые и достаточные условия управляемости и наблюдаемости имеют вид det Wc¹0, det Wo¹0.
1.3 Анализ минимальности моделей. Одной и той же передаточной функции Q (p) можно сопоставить целый класс эквивалентных реализаций в пространстве состояний, характеризуемых различными тройками матриц (A, b, c) разных, вообще говоря, размеров. Реализация называется минимальной, если размер ее матрицы A наименьший среди всех эквивалентных реализаций. Поиск такой реализации имеет практический смысл, так как ее моделирование на ЭВМ требует меньших вычислительных затрат. Для анализа минимальности реализации нужно проверить ее управляемость и наблюдаемость. К ритерийминимальности. Для того чтобы реализация (3) была минимальной, необходимо и достаточно, чтобы она была управляемой и наблюдаемой одновременно. Таким образом, анализ минимальности конкретной реализации сводится к проверке пары критериев rankR= n, rankD= n. Если хотя бы один из рангов меньше n, то реализация неминимальна. Размерность эквивалентной минимальной реализации n0 определяется по формуле n 0= rank(RD). Анализ минимальности с помощью грамианов управляемости и наблюдаемости проводится аналогично. Критерием минимальности служит выполнение условия det(WcWo)¹0, эквивалентного паре условий det Wc¹0, det Wo¹0. Если исходное описание реализации оказалось неминимальным, то возникает задача перехода к минимальной реализации. Чтобы решить ее, сначала перейдем от описания в пространстве состояний (3) к передаточной функции
Далее нужно выделить общий множитель в числителе и знаменателе передаточной функции Q (p) и сократить на него. Эта процедура известна, как сокращение совпадающих нулей и полюсов системы. Отметим ряд соотношений между элементами матриц А, b, c и коэффициентами передаточной функции, вытекающих из формулы (4),. Знаменатель передаточной функции совпадает с характеристическим полиномом матрицы А
А(p)=det(p E-A) = pn + an - 1 pn -1 +...+ a 1 p + a 0.
Его корни l 1,..., l n равны собственным числам матрицы А, а коэффициенты а 0 и an- 1 с точностью до знака равны ее определителю и следу
Старший и младший коэффициенты числителя передаточной функции
В(p)= bn - 1 pn -1 +...+ b 1 p + b 0 удовлетворяют соотношениям bn -1 = cb, b 0/ a 0= - c A-1 b. (6)
Величина k 0= b 0/ a 0 называется статическим коэффициентом усиления. Она равна установившемуся значению переходной функции системы. В пакете MATLAB для вычисления статического коэффициента усиления имеется команда dcgain (от direct current gain – коэффициент усиления по постоянному току). В ее основу положена формула k 0=Q(0). Приведенные соотношения удобно использовать для контроля вычислений. Получение минимальной реализации в пакете MATLAB осуществляется командой minreal, для вычисления нулей и полюсов можно использовать функции zero, pole, pzmap, zpk. Аргументом во всех случаях служит исследуемая система sys, предварительно сформированная командами ss или tf.
2. ЗАДАНИЕ ПО РАБОТЕ И СОДЕРЖАНИЕ ОТЧЕТА
1. Нарисовать схему рис.2 для своего варианта и найти ее передаточную функцию по формуле (1). 2. Проверить устойчивость системы, используя алгебраический и корневой критерии. 3. Получить для своего варианта схемы описание в пространстве состояний вида (3) и выписать матрицы A, В, С. 4. Найти матрицы управляемости и наблюдаемости системы, определить их ранги и сделать вывод об управляемости, наблюдаемости и минимальности системы. 5. Найти передаточную функцию по формуле (4), и сравнить ее с полученной в п.1. Проверить выполнение соотношений (5), (6). Тремя способами (по структурной схеме, передаточной функции и описанию в пространстве состояний) найти статический коэффициент усиления системы. 6. Определить порядок минимальной реализации и найти ее передаточную функцию, выполнив сокращение нулей и полюсов. Найти реакцию минимальной реализации на единичный скачок и построить ее график. 7. Привести программы на языке MATLAB для выполнения пунктов 2 – 6 и краткое описание назначения и синтаксиса команд rank, ss, tf, zpk, zero, pole, pzmap, ctrb, obsv, minreal, dcgain.
3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. В диалоговом режиме пакета MATLAB ввести матрицы A, b, c и сформировать ss-описание системы sys=ss(A, b, c, 0). Используя команды pole, eig, pzmap, найти полюсы системы и получить график их расположения на комплексной плоскости. Сделать вывод об устойчивости. Построить диаграмму Найквиста системы и сделать заключение об устойчивости системы, охваченной обратной связью (рис.1). 2. Найти матрицы управляемости и наблюдаемости, вычислить их определители и ранги. Сделать вывод об управляемости, наблюдаемости и минимальности. Найти грамианы управляемости и наблюдаемости. 3. С помощью команд tf и zpk перейти к передаточной функции. Двумя способами получить минимальную реализацию (сокращая нули и полюса, и с помощью команды minreal). Сравнить переходные функции исходной и минимальной реализаций, а также их статический коэффициент усиления. 4. Набрать схемы исходной и минимальной реализаций в SIMULINK и сравнить их реакции на одинаковые входные сигналы.
4. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Найти передаточные функции систем, заданных в пространстве состояний тройкой матриц:
2. Найти ранги матриц управляемости и наблюдаемости для систем из п.1. 3. Нарисовать структурные схемы систем, матрицы которых приведены ниже.
Определить, какие из них являются: а) устойчивыми; б) управляемыми; в) наблюдаемыми; г) минимальными. 4. Система управления задана структурной схемой, показанной на рис. 3.
Требуется: а) найти статический коэффициент усиления схемы; б) найти передаточную функцию схемы и проанализировать ее устойчивость; в) найти описание схемы в пространстве состояний; построить матрицы управляемости и наблюдаемости, сделать вывод о минимальности; г) выяснить, при каких значениях коэффициента k схема будет устойчивой, управляемой, наблюдаемой.
5. ВАРИАНТЫ ЗАДАНИЙ
Практическая работа №5
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-11-02; просмотров: 957; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.227.194 (0.186 с.) |

 , связывающую изображения по Лапласу входного и выходного сигналов.
, связывающую изображения по Лапласу входного и выходного сигналов.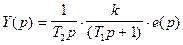 ,
,  (1)
(1)

 .
. 
 (2)
(2) , где С 1 и С 2 - коэффициенты, зависящие от начальных условий и определяемые в дальнейшем. Если корни одинаковые (кратные) p 1 =p 2, то решение имеет вид
, где С 1 и С 2 - коэффициенты, зависящие от начальных условий и определяемые в дальнейшем. Если корни одинаковые (кратные) p 1 =p 2, то решение имеет вид  . Паре комплексных корней p 1,2 = a ± j b соответствует решение
. Паре комплексных корней p 1,2 = a ± j b соответствует решение 
 постоянные С1 и С2 находятся из системы уравнений
постоянные С1 и С2 находятся из системы уравнений
 То уравнение примет следующий вид
То уравнение примет следующий вид 



 .
. откуда А=1.5.
откуда А=1.5.
 Подставив начальные условия
Подставив начальные условия 
 в оба уравнения получим:
в оба уравнения получим: и
и 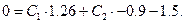


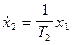 .
.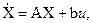
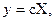
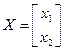 ,
,  ,
,  ,
, 
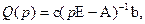 (3)
(3) (4)
(4) с нулевыми начальными условиями следует набрать код
с нулевыми начальными условиями следует набрать код и построить график выходного сигнала.
и построить график выходного сигнала.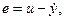


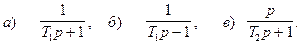

 ,
, неустойчиво, так как 2×0,5<1×3.
неустойчиво, так как 2×0,5<1×3.


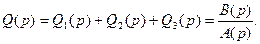 (1)
(1) (2)
(2) (3)
(3)




 ,
, 
 .
. (4)
(4)




