
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ І. Моделі та методи лінійного, дискретного та динамічного програмуванняСтр 1 из 8Следующая ⇒
Вступ
Дослідження операцій – науковий напрямок, метою якого є розробка методів аналізу цілеспрямованих дій (операцій) та об’єктивна (частіше кількісна) порівняльна оцінка рішень. Предметом дослідження операцій є системи – взаємодіюча сукупність елементів, призначених для досягнення певної мети (або цілі). Методом дослідження операцій є моделювання. Моделювання – один із загально-наукових методів дослідження, що застосовується для аналізу та синтезу систем. Це спосіб дослідження, коли замість реального об’єкту вивчається його умовний образ – модель. Модель – це умовний образ об’єкту чи процесу, який вивчається, та відображає його основні характеристики і використовується в ході дослідження. Конструювання моделі на основі попереднього вивчення об’єкту, з’ясування його суттєвих характеристик, експериментальний та (або) теоретичний аналіз моделі, порівняння результатів з даними про об’єкт, коректування моделі складають зміст методу моделювання. Припущенням відносно більшої доступності моделі для аналізу у порівнянні з реальним об’єктом є те, що моделювання, як правило, приводить до спрощенного образу об’єкта. Існує багато підходів до класифікації моделей. В залежності від засобів моделювання моделі можна поділити на абстрактні (концептуальні) та матеріальні (фізичні). Математичні моделі відносяться до абстрактних. Математична модель – система математичних виразів, які описують характеристики об’єкта моделювання та взаємозв’язки між ними. У підручнику розглядається математичне моделювання саме соціально-економічних систем та процесів. Класифікацію самих економіко-математичних моделей можна робити за різними ознаками, основними з яких є: 1) за цільовим призначенням – теоретико-аналітичні та прикладні моделі; 2) за ступінню агрегованості об’єктів – макроекономічні (функціонування економіки як єдиного цілого) та мікроекономічні (підприємства, фірми) моделі; 3) за призначенням – балансові (відповідність між запасами, ресурсами та їх використанням), трендові (моделювання на основі вивчення тенденцій розвитку), оптимізаційні (вибір найкращого рішення), імітаційні (імітація поведінки об’єкту, який вивчається) моделі;
4) за характером інформації – детерміновані (на базі фіксованих значень вхідних даних) та стохастичні (вхідні дані є випадковими величинами) моделі; 5) за характеристикою математичного апарату – лінійного та нелінійного програмування, дискретного та стохастичного програмування, кореляційно-регресійні моделі, моделі теорії масового обслуговування, моделі сітьового планування та управління тощо; 6) за підходом до вивчення системи – дескриптивні та нормативні моделі. Слід зазначити, що ефективне управління соціально-економічними системами не завжди зводиться до побудови економіко-математичних моделей та виконання відповідних обчислень. У процесі формування управлінських рішень інколи треба враховувати суттєві фактори, які не піддаються математичній формалізації, наприклад, деякі психологічні аспекти людського фактору, і тому – економіко-математичне моделювання є однією з важливих компонент системного аналізу, планування й ефективного управління економічними системами. Успішне застосування дослідження операцій у теоретичних та практичних дослідженнях будь-яких систем, в тому числі соціально-економічних, можливе за умови існування чотирьох взаємозв’язуваних факторів: - методів конструювання оптимізаційних моделей; - методів розв’язування оптимізаційних задач; - методів якісного, економіко-математичного аналізу; - методів інформаційного забезпечення. Таким чином, теорія дослідження операцій охоплює всі етапи дослідження систем: - ідентифікація проблеми (формування проблеми, мети її розв’язання, виявлення умов та обмежень); - побудова оптимізаційної моделі (встановлення математичних співвідношень між метою розв’язання проблеми та існуючими обмежуючими факторами); - інформаційне наповнення моделі; - знаходження розв’язку сформульованої задачі; - аналіз моделі на чутливість щодо змін вхідних параметрів системи; - перевірка адекватності моделі (модель можна вважати адекватною, якщо рішення, яке отримали на її основі, здатне достатньо надійно передбачити поведінку системи); - реалізація отриманих та відповідним чином перевірених рішень для аналізу, планування або управління системою.
Математичні моделі, які вивчаються в теорії дослідження операцій, відносяться до нормативних, оптимізаційних. Задачі та методи дослідження розбиваються на окремі класи в залежності від типу операцій та процесу, для аналізу яких вони використовуються. Тому курс „Дослідження операцій” складається з наступних розділів: математичне програмування, імітаційне моделювання, теорія ігор, теорія управління запасами, сітьове планування та теорія масового обслуговування. В загальному вигляді оптимізаційна задача дослідження операцій полягає у знаходженні екстремума функції:
за умов
Функція Умови задачі (2) називаються обмеженнями задачі і утворюють множину допустимих альтернативних управлінських рішень. Оптимізаційні задачі дослідження операцій розв’язуються методами математичного програмування. Математичне програмування – це розділ математики, який розробляє теорію та методи розв’язування екстремальних задач типу (1), (2). Розв’язати задачу математичного програмування означає знайти таке з альтернативних рішень, яке б було найкращим з точки зору значення цільової функції. В залежності від характеру математичної функції, всі задачі математичного програмування діляться на лінійні та нелінійні. Якщо цільова функція В залежності від характеру змінних, задачі математичного програмування діляться на дискретні та неперервні. Дискретними називаються задачі, в яких хоча б одна з змінних може набувати лише дискретних значень. Окремий клас дискретних задач становлять задачі, в яких змінні набувають цілочисельних значень. Такі задачі називаються задачами цілочисельного програмування. Якщо змінні можуть набувати будь-яких значень на певних інтервалах, тоді такі задачі називаються неперевними. В залежності від характеру вхідних даних задачі математичного програмування діляться на детерміновані та стохастичні. При побудові детермінованих моделей вважається, що для дослідження економічних систем чи процесів випадкові події не відіграють істотної ролі і вхідні дані точно визначені. У протилежному випадку математична модель має враховувати випадковий характер вхідних даних у вигляді функції розподілу. Така оптимізаційна задача відноситься до стохастичних. Окремий тип задач складають динамічні задачі. У таких задачах вдається для кожної змінної сформулювати локальну оптимізаційну задачу, в результаті розв’язування якої, знаходиться значення відповідної змінної, найкраще з точки зору всієї задачі. Таким чином, математичне програмування, як теорія методів розв’язування екстремальних задач виду (1) – (2), в залежності від типу задач поділяється на наступні підрозділи: - лінійне програмування; - нелінійне програмування; - дискретне програмування; - динамічне програмування; - стохастичне програмування. Дослідження соціально-економічних об’єктів та процесів методом моделювання передбачає їх математичну формалізацію – побудову математичної моделі. Побудова математичної моделі здійснюється на другому етапі дослідження операцій після визначення на змістовному рівні мети дослідження, а також набору показників, які достатньо повно характеризують об’єкт або процес.
Процедура побудови математичних моделей є загальною для всіх задач математичного програмування і складається з таких кроків: - ідентифікація керованих змінних; - запис цільової функції через змінні задачі; - запис обмежень через змінні задачі. Розглянемо приклади побудови задач математичного програмування. Приклад. Завод виробляє мінеральну воду у пляшках по півлітра, одному, півтора та два літри. Виробництво обмежено запасом мінеральної води на заводі – 10 т, а також виробничими потужностями обладнання, яке дозволяє щодня випускати не більше 5 тис. пляшок. Прибуток від реалізації кожної півлітрової пляшки мінеральної води складає 20 коп., однолітрової – 18 коп., півторалітрової – 16 коп. та дволітрової – 15 коп. Скільки пляшок мінеральної води має щодня виробляти завод з точки зору максимізації прибутку. Визначимо змінні задачі. В результаті розв’язання задачі повинно бути прийняте рішення щодо виробництва кожного виду пляшок. Тоді змінні задачі – кількість пляшок певного виду: План виробництва мінеральної води буде тим кращим, чим більший прибуток він буде забезпечувати. Тому цільова функція через змінні задачі визначаються як 0,2 і означає величину прибутку, яку треба максимізувати. Але як завгодно великий прибуток від реалізації мінеральної води завод отримати не може, тому що при визначенні плану необхідно враховувати умови виробництва. Однією з таких умов є запас мінеральної води. Через змінні задачі витрати мінеральної води описуються як 0,5 Максимальна кількість розлитої у пляшки мінеральної води не повинна перевищувати 10 т, тому перше обмеження задачі має вигляд: 0,5 Другою умовою – є виробничі потужності обладнання, які не дозволяють щодня випускати більше 5 тис. пляшок. Тому друге обмеження задачі –
Інших умов немає, але необхідно врахувати, що кількість пляшок у плані виробництва повинна бути невід’ємною, а також цілим числом. Таким чином математична модель має наступний вигляд: 0,2 0,5
Приклад. Інвестиційна компанія розглядає можливість інвестицій в акції трьох підприємств з метою отримання прибутку не менше 500 тис. грн. при мінімальних витратах. Акції першого підприємства дозволять отримати 20% прибутку від вартості, другого – 22%, а третього – 25%. Вартість однієї акції кожного підприємства відповідно дорівнює: 1тис. грн., 1,5 тис. грн. та 1,4 тис. грн. Кількість кожного виду акцій обмежена відповідно: 10 тис.шт., 20 тис. шт. та 8 тис. шт. Побудуємо модель для знаходження оптимального варіанту інвестицій. Введемо змінні 1000 за умов забезпечення необхідного рівня прибутку 0,2 врахування обмежень на кількість акцій
і невід’ємності та цілочисельності змінних
Розглянуті приклади відносяться до лінійних задач з цілочисельними змінними. Приклад. Менеджер з цінних паперів вирішив розмістити 100 тис. грн. таким чином, щоб отримати максимальний річний прибуток. Його вибір обмежений трьома видами вкладів: в облігації внутрішньої державної позики (ОВДП), в акції фабрики та в екологічний проект. Доходність кожного виду вкладів описується залежностями Перший вид вкладів відноситься до безризикових, а інші – ризикові. Враховуючи можливі зміни у політиці уряду, менеджер вважає, що не більше 75% вкладів треба розмістити у ризикові. Побудуємо модель оптимального розподілу вкладів. Змінні моделі Цільова функція задачі – величина прибутку, яку треба максимізувати:
за умов загальної вартості всіх вкладів
вимог щодо величини ризикових вкладів
а також, враховуючи зміст змінних, їх невід’ємності
Побудована модель відноситься до нелінійних задач, так як цільова функція описується нелінійною функцією. Розглянемо приклад постановки задачі, в якій вхідні дані є випадковими величинами. Приклад. Агрофірма займається вирощуванням капусти, помідорів, огірків та моркви. Посівна площа обмежена Розмір площі, яка виділяється під певний вид овочів, позначимо за змінні задачі
Тоді кількість комплектів овочів визначається як
де Цільова функція моделі розподілу площ – максимальна кількість комплектів овочів.
обмеження: по загальній площі агрофірми
та по знаку змінних
Побудована модель відноситься до задач стохастичного програмування. В усіх наведених прикладах цільову функцію треба було максимізувати. Напрямок цільової функції залежить від конкретної постановки задачі. Наприклад, якщо оптимальне рішення повинно прийматися з точки зору транспортних витрат або ступеня ризику, тоді цільова функція задачі повинна прямувати до мінімума. Приклади такого типу задач наводяться в різних главах підручника. Імітаційне моделювання як метод моделювання економічних систем, що базується на проведенні машинних експериментів (імітацій) є однією з основних складових частин дослідження операцій. Аналіз моделей вибору рішення в конфліктних ситуаціях або в ситуаціях невизначеності є предметом важливого розділу дослідження операцій – теорії ігор. Зміст математичної теорії ігор полягає, по-перше, у визначенні принципів оптимальної поведінки гравців, по-друге, в розробці методів знаходження їх оптимальних стратегій. Застосування теорії ігор можливе в принципі в усіх сферах діяльності, в тому числі, і в економіці, наприклад, при визначенні стратегії поведінки фірми на ринку. Одним з важливих розділів дослідження операцій є теорія управління запасами. На основі моделей та методів управління запасами визначаються схеми поповнення запасів, при яких забезпечуються мінімальні сумарні витрати, пов’язані з поповненням та зберіганням продукції та збитками від незадоволення попиту. Оптимальний рівень запасів залежить від багатьох умов, що пов’язані з інтенсивністю використання запасів, можливостями зберігання, витратами на утримання запасів. На рівень запасів мають вплив також коливання попиту на продукцію, можливості постачальників, оперативність поповнення запасів, а також витрати на перевезення. Методи дослідження операцій, що базуються на використанні сітьових моделей проектів, програм або розробок, розглядаються у такому розділі дослідження операцій як сітьове планування та управління. Моделі та методи сітьового планування та управління призначені для розв’язування двох основних проблем: формування календарного плану реалізації проектів та прийняття ефективних рішень у процесі його виконання. Прикладні задачі теорії масового обслуговування пов’язані з дослідженням будь-яких операцій, які складаються із багатьох однорідних елементарних операцій, на здійснення яких впливають випадкові фактори. Тому теорія масового обслуговування є складовою частиною дослідження операцій. Підручник складається з шести частин – „Математичне програмування”, „Імітаційне моделювання”, „Теорія ігор”, „Теорія управління запасами”, „Сітьове планування та управління” та „Теорія масового обслуговування”, в кожній з яких викладаються теоретичні основи розв’язування відповідного типу задач, розглядаються приклади їх застосування, даються завдання для самостійної роботи та контрольні запитання. Особливістю підручника є також представлення сучасних пакетів прикладних програм, які використовуються в дослідженні операцій. Підручник містить термінологічний словник.
Таблиця 1.1.
Математична модель цієї задачі має такий вигляд
Приклад 1.5.
Рис. 1.2. На рис.1.2 допустима множина Приклад 1.6.
У цьому прикладі допустима область
Рис. 1. 3. Аналізуючи рис.1.3, приходимо до висновку, що максимальне значення цільової функції дорівнює 9, а оптимальний розв’язок — будь-яка точка сторони Множину точок, які належать до відрізку Геометричне розв’язування ЗЛП з трьома змінними стає менш наочним, а у разі більшої кількості змінних - навіть неможливим. Проте геометричне розв’язування найпростіших задач лінійного програмування ілюструє деякі важливі властивості лінійних оптимізаційних задач з будь-якою кількістю змінних. Зокрема, для ЗЛП на максимум (мінімум) тоді і тільки тоді має оптимальний розв’язок, коли її цільова функція обмежена зверху (знизу) у допустимій множині. Далі побачимо, що особливу роль при дослідженні та розв’язуванні ЗЛП відіграють вершини допустимої множини. При Ще одна істотна властивість ЗЛП полягає в тому, що розв’язок задачі, коли він існує, досягається, як правило, на межі допустимої множини. Більш того, якщо допустима множина ЗЛП має вершини, то принаймні одна з них відповідає оптимальному плану. Строге доведення цих властивостей подамо у наступному пункті.
Доведення. Нехай Теорема 1.3.1. Допустима множина ЗЛП опукла (якщо вона непорожня). Доведення. Оскільки допустима множина Окремим обмеженням ЗЛП може бути або гіперплощина, або півпростір. Нехай Тоді для будь-якої точки
тобто Аналогічно для півпростору. Нехай
тобто Теорема 1.3.2. Множина оптимальних точок допустимої множини ЗЛП опукла (якщо вона непорожня). Доведення. Якщо оптимальна точка єдина, то теорема вірна в силу нашої умови вважати опуклою множину, що складається з однієї точки. Нехай оптимальних точок більше ніж одна. Візьмемо дві з них, Нехай Розглянемо будь-яку точку Тоді
Отже, З теореми 1.3.2 випливає, що множина оптимальних точок не може бути скінченною, якщо оптимальна точка не єдина. Теорема 1.3.3. Якщо цільова функція ЗЛП на максимум (мінімум) обмежена зверху (знизу) на допустимій множині, то ця задача має оптимальний розв’язок. Назвемо тепер многогранною множиною перетин скінченого числа півпросторів. Обмежена многогранна множина називається многогранником. Очевидно, що допустима область Вершиною опуклого многогранника у просторі Тобто Лема 1.3.2. Будь-яка точка опуклого обмеженого многогранника є опуклою лінійною комбінацією його вершин. Тобто, якщо
Теорема 1.3.4. Якщо допустима множина Доведення. Нехай Припустимо, що
Нехай
Далі
де З (1.3.1) випливає, що Теорему доведено. Розглянута властивість дає важливу ідею розв’язування ЗЛП — перебір вершин її допустимої множини. Але такий шлях розв’язування ЗЛП, навіть з відносно невеликим числом обмежень і невідомих, практично нездійсненний, оскільки процес відшукування вершин досить трудомісткий, а число вершин многогранника може бути досить великим. Тому на початку 50-х років було винайдено американським математиком Дж.Данцигом досить раціональний спосіб перебору вершин: симплекс-метод або метод послідовного поліпшення плану для розв’язування задач лінійного програмування [14]. Нехай розглядається задача з непорожньою допустимою множиною. Загальна ідея симплекс-методу: 1) тим чи іншим способом знаходиться одна з вершин допустимої області 2) по певному правилу перевіряється, чи не можна стверджувати, що задача не має оптимальних розв’язків (цільова функція необмежена зверху або, відповідно, знизу на допустимій множині); якщо стверджувати це можна, то задача нерозв’язувана; якщо не можна, то 3) по певному правилу шукаємо нову, ліпшу з точки зору значення цільової функції вершину і повертаємося на 1-й крок. Далі розглянемо строге обгрунтування симплекс-методу для невироджених задач лінійного програмування. Симплекс-метод Доведення. Необхідність. Нехай Тоді Доведемо необхідність від супротивного, а саме, припустимо, що Але тоді
З (1.4.2) отримаємо
За умовою, Достатність. Нехай Нам треба довести, що
За умовою
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 893; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.44.108 (0.147 с.) |
 (1)
(1)
 , (2)
, (2) .
. та функції обмежень задачі
та функції обмежень задачі 
 - кількість півлітрових пляшок,
- кількість півлітрових пляшок,  - кількість однолітрових,
- кількість однолітрових,  - півторалітрових,
- півторалітрових,  - дволітрових.
- дволітрових. 10000.
10000. 5000.
5000.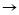 max,
max, 0,
0, - цілі.
- цілі. (
( 1, 2, 3), які означають кількість акцій відповідно першого, другого та третього підприємства. Критерієм якості інвестицій будуть найменші витрати. Тоді цільова функція задачі -
1, 2, 3), які означають кількість акцій відповідно першого, другого та третього підприємства. Критерієм якості інвестицій будуть найменші витрати. Тоді цільова функція задачі - 1000
1000  500000,
500000,

 та
та  , де
, де  (
( =100000,
=100000,
 га. Урожайність овочів, як відомо, підпадає під вплив погодних умов, тому точне значення передбачити неможливо і слід розглядати як випадкові величини. Маркетингові дослідження свідчать, що попит на овочі має певні пропорції:
га. Урожайність овочів, як відомо, підпадає під вплив погодних умов, тому точне значення передбачити неможливо і слід розглядати як випадкові величини. Маркетингові дослідження свідчать, що попит на овочі має певні пропорції:  % - капуста,
% - капуста, 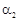 % - помідори та по
% - помідори та по  % - огірки та морква. (
% - огірки та морква. ( (
( - стан погоди.
- стан погоди. ,
, – математичне сподівання.
– математичне сподівання.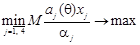 ,
,
 .
.


 )
450 (
)
450 ( )
260 (
)
260 ( )
)
 )
8 (
)
8 ( )
6 (
)
6 ( )
)
 )
14 (
)
14 (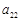 )
13 (
)
13 (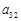 )
)
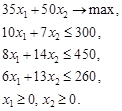


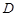 не обмежена. Значення
не обмежена. Значення  ліній рівня функції
ліній рівня функції  будуть зменшуватись при переміщенні у напрямку, протилежному градієнту. Очевидно, що
будуть зменшуватись при переміщенні у напрямку, протилежному градієнту. Очевидно, що  і задача не має оптимального розв’язку (цільова функція не обмежена знизу).
і задача не має оптимального розв’язку (цільова функція не обмежена знизу).

 чотирикутника
чотирикутника  .
. за умови
за умови  , де числа
, де числа  та
та  - координати по осі
- координати по осі  точок відповідно
точок відповідно 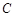 та
та 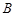 . Або межі по змінній
. Або межі по змінній  , де
, де  та
та  - координати по осі
- координати по осі 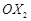 точок відповідно
точок відповідно  можна також описати так:
можна також описати так:  , де
, де 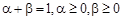 . Тоді
. Тоді  .
. геометрично очевидно необхідні і достатні умови існування оптимального розв’язку, а саме:
геометрично очевидно необхідні і достатні умови існування оптимального розв’язку, а саме: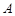 і
і  . Тоді
. Тоді 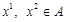 і
і 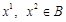 . З означення опуклої множини
. З означення опуклої множини  і
і 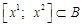 . Отже
. Отже  , а це і означає, що
, а це і означає, що 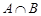 — опукла множина.
— опукла множина.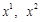 — довільні точки такі що
— довільні точки такі що 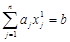 і
і 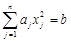 .
.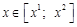
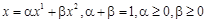 ,
,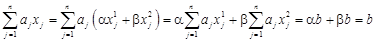 ,
, належить гіперплощині.
належить гіперплощині.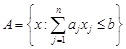 і
і  і
і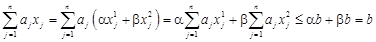 ,
,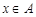 і
і 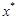 і
і  .
.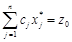 і
і  — оптимальне значення цільової функції.
— оптимальне значення цільової функції.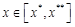 :
:  . Очевидно, що
. Очевидно, що 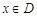 .
.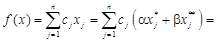
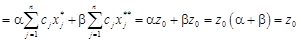 .
.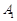 — многогранна множина. Надалі область
— многогранна множина. Надалі область 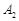 називається будь-яка точка, яка не є внутрішньою точкою ніякого відрізка, що цілком належить цьому многограннику.
називається будь-яка точка, яка не є внутрішньою точкою ніякого відрізка, що цілком належить цьому многограннику.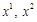 таких що
таких що  ,
,  і
і  , де
, де 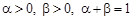 .
.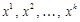 — вершини многогранника
— вершини многогранника  .
.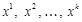 — вершини допустимого многогранника
— вершини допустимого многогранника 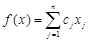 за умови
за умови  . Тоді
. Тоді .
.
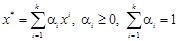 .
. ,
,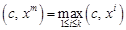 .
.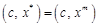 , а це і означає, що існує вершина
, а це і означає, що існує вершина 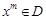 , у якій цільова функція
, у якій цільова функція 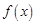 набуває найбільшого значення.
набуває найбільшого значення. .
.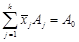 і
і  — лінійно незалежні вектори.
— лінійно незалежні вектори.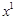 і
і  такі що
такі що  і
і  .
. ,
,  і
і .
.
 .
. , а це означає, що
, а це означає, що  , то
, то  і
і  .
. , не всі нульові і такі що
, не всі нульові і такі що .
.



