
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обгрунтування симплекс-методу для невироджених задач лінійного програмування
Нехай дана задача лінійного програмування у канонічному виді:
Або у векторній формі
де Припустимо, що задача (1.4.1) має допустимий розв’язок і ранг матриці Якщо Припустимо, що Введемо необхідні означення. Ненульовий допустимий розв’язок Набір векторів Максимальне число лінійно незалежних векторів дорівнює Базисом базисного розв’язку назвемо упорядкований набір з Оскільки невироджений базисний розв’язок містить рівно Приклад 1.7. Нехай обмеження ЗЛП мають вигляд
В цьому прикладі Допустимими розв’язками будуть, наприклад, такі вектори:
Вектори Для Для Для базисного невиродженого розв’язку Теорема 1.4.1. Вектор Доведення. Необхідність. Нехай Тоді
Доведемо необхідність від супротивного, а саме, припустимо, що Але тоді
З (1.4.2) отримаємо
За умовою, Достатність. Нехай Нам треба довести, що
За умовою
Помноживши ліву і праву частини рівності (1.4.3) на
Вибираючи
допустимі розв’язки ЗЛП (1.4.1). Крім того, Але тоді З теореми 1.4.1 випливає скінченність числа вершин многогранника допустимих розв’язків будь-якої ЗЛП. Кожній вершині відповідає певна лінійно незалежна підсистема системи векторів Перехід від однієї вершини до іншої — це перехід від одного базисного розв’язку до іншого. Лема 1.4.1. Нехай дано систему
її базис. Замінимо у цьому базисі який-небудь з векторів
за базисом Доведення. Необхідність. Якщо Достатність. Нехай
Зауважимо, що
Тобто, для вектора
Знайдемо тепер координати усіх векторів
Нехай
Нехай
Тоді
Так
Для введеного до базису вектора
Формули (1.4.9) також можна отримати із загальних (1.4.10). Дійсно, для
Тоді
Надалі коефіцієнт Тоді При обчисленнях нових координат зручно користуватися таблицями (табл.1.2). Тут у клітинках наведені відповідні координати вектора, до якого відноситься даний стовпець, у старому базисі; вертикальною стрілкою (зверху) відмічено вектор ( Таблиця 1.2.
Щоб отримати Для того, щоб у відповідності з формулами (1.4.10) отримати будь-яку, наприклад, Елементи головної діагоналі перемножуються (причому у ведучій клітинці використовується нове значення 1) і з цього добутку віднімається добуток елементів додаткової діагоналі (причому у відповідній клітинці ведучої строчки знову береться нове значення). Тобто, Приклад 1.8. Нехай
Вектори Базисна матриця, складена з векторів
Координати будь-якого вектора
де
Координати базисних векторів Отже,
Підрахуємо тепер координати векторів
Переконаємося, що заміна у початковому базисі вектора
У нашому випадку Тоді координати векторів
Координати базисних векторів відомі.
Проводячи обчислення по таблиці прийдемо до тих же результатів: Таблиця 1.3.
Координати векторів у новому базисі наведені у таблиці 1.4. Таблиця 1.4.
Введемо поняття оцінки вектора. Нехай вектори
Для усіх базисних векторів оцінки дорівнюють нулеві. Дійсно, якщо Нехай дана КЗЛП (1.4.1) і припустимо, що всі її базисні розв’язки невироджені. Надалі назвемо ЗЛП невиродженою, якщо всі її базисні розв’язки невироджені. Теорема 1.4.2. (про можливість поліпшення базисного розв’язку) Якщо для даного невиродженого базисного розв’язку задачі (1.4.1) існує така від’ємна оцінка
Доведення. Нехай
Оскільки Координати вектора
де Для того, щоб новий базисний розв’язок
Згідно умов теореми і враховуючи, що Якщо ж
Знайдемо тепер значення цільової функції при новому базисному розв’язку:
Додаючи до цієї суми
Або Оскільки Теорема 1.4.2 дає достатні умови того що є кращий, ніж даний, розв’язок задачі, і правило для знаходження відповідного базису. Що можна сказати про існування кращого базисного розв’язку чи про можливість розв’язання задачі, якщо порушуються умови теореми: або всі оцінки Теорема 1.4.3. (критерій оптимальності базисного розв’язку) Якщо для даного базисного розв’язку всі оцінки Доведення. Нехай Візьмемо інший допустимий розв’язок Якщо б інших допустимих розв’язків не було, тоді єдиний допустимий розв’язок Покажемо, що Оскільки
Оскільки
Але
Але ж
Оскільки розклад будь-якого вектора по базису єдиний, то
Підставляючи це в (1.4.12), дістанемо
що і треба було довести. Теорема 1.4.4. (ознака необмеженості цільової функції) Якщо для якого-небудь базисного розв’язку існує хоча б одна оцінка Доведення. Нехай, наприклад, Розглянемо вектор Вектор
Підрахуємо тепер значення цільової функції для побудованого допустимого розв’язку
Оскільки Зауваження. Теореми 1.4.3 та 1.4.4 справедливі і без припущення невиродженості базисних розв’язків. Дійсно, легко бачити по доведенням, що фактично використовувалась не умова Розглянемо тепер випадок, коли умови теореми 1.4.2 не виконані: хоча і є Покажемо, що якщо дана задача невироджена (що ми і припускали), то такого випадку просто не може бути. Дійсно, нехай
Оскільки
Очевидно, що Хоч розв’язок, що відповідає новому базису, і допустимий, він виявляється виродженим, бо принаймні одна з його базисних координат ( Отже, для невироджених ЗЛП можливі лише три випадки: 1. Усі 2. Існує
3. Існують оцінки
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 557; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.47.253 (0.167 с.) |
 ,
,  ,
,  , …
, … 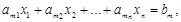 ,
,  .
.
 ,
,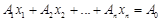 ,
, ,
, ,
,  .
. дорівнює
дорівнює  . Якщо
. Якщо  , то це твердження не має сенсу.
, то це твердження не має сенсу.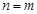 , то задача (1.4.1) має єдиний розв’язок (ранг дорівнює
, то задача (1.4.1) має єдиний розв’язок (ранг дорівнює  ) і цей розв’язок буде оптимальним. Тобто при
) і цей розв’язок буде оптимальним. Тобто при  .
. задачі (1.4.1) називається базисним або опорним, якщо вектори
задачі (1.4.1) називається базисним або опорним, якщо вектори  , які відповідають відмінним від 0 координатам
, які відповідають відмінним від 0 координатам  , лінійно незалежні.
, лінійно незалежні. називається лінійно незалежним, якщо умова
називається лінійно незалежним, якщо умова  виконується лише при
виконується лише при 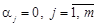 .
. ,
,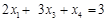 ,
, .
. .
. .
.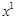 та
та  - базисні розв’язки, вектор
- базисні розв’язки, вектор  не є базисним розв’язком.
не є базисним розв’язком. зв’язаний з додатною координатою. Цей розв’язок вироджений і його базисом можуть бути пари векторів:
зв’язаний з додатною координатою. Цей розв’язок вироджений і його базисом можуть бути пари векторів: 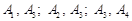 .
. і цей розв’язок невироджений. Матрицю, утворену з базисних векторів, будемо називати базисною матрицею і позначати через
і цей розв’язок невироджений. Матрицю, утворену з базисних векторів, будемо називати базисною матрицею і позначати через 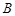 . Визначник базисної матриці не повинен дорівнювати нулю.
. Визначник базисної матриці не повинен дорівнювати нулю. .
. — вершина допустимого многогранника.
— вершина допустимого многогранника.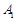 координат більші нуля, тобто
координат більші нуля, тобто  .
.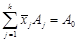 і
і  — лінійно незалежні вектори.
— лінійно незалежні вектори.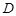 . Тоді існують точки
. Тоді існують точки  і
і  .
. ,
,  і
і .
.
 .
. , тоді для деяких
, тоді для деяких  , а це означає, що
, а це означає, що  , то
, то  і
і  .
. , не всі нульові і такі що
, не всі нульові і такі що .
.
 .
.
 і додаючи до (1.4.4), дістанемо
і додаючи до (1.4.4), дістанемо (
( - параметр).
- параметр). , дістанемо, що вектори
, дістанемо, що вектори і
і -
- не є вершиною. Прийшли до протиріччя. Отже,
не є вершиною. Прийшли до протиріччя. Отже,  . При цьому різним вершинам відповідають різні підсистеми. Оскільки число різних підсистем скінченої системи векторів
. При цьому різним вершинам відповідають різні підсистеми. Оскільки число різних підсистем скінченої системи векторів  -
-
 деяким вектором
деяким вектором 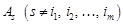 з початкової системи. Тоді
з початкової системи. Тоді  також базис тоді і тільки тоді, коли у розкладі
також базис тоді і тільки тоді, коли у розкладі
 коефіцієнт при
коефіцієнт при  .
. , тоді
, тоді 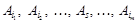 — лінійно залежні і не можуть бути базисом. Отже,
— лінійно залежні і не можуть бути базисом. Отже,  (причому, хоча б один з цих коефіцієнтів відмінний від нуля) такі що
(причому, хоча б один з цих коефіцієнтів відмінний від нуля) такі що .
. , інакше б вектори
, інакше б вектори  були б лінійно залежними, а це неможливо, бо ці вектори складають частину базису (1.4.5). Тоді
були б лінійно залежними, а це неможливо, бо ці вектори складають частину базису (1.4.5). Тоді .
.
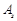 існує інший, відмінний від (1.4.6), розклад по базису (1.4.5). У розкладі (1.4.7) коефіцієнт при
існує інший, відмінний від (1.4.6), розклад по базису (1.4.5). У розкладі (1.4.7) коефіцієнт при  дорівнює нулю, а у розкладі (1.4.5)
дорівнює нулю, а у розкладі (1.4.5)  — лінійно незалежні і утворюють базис.
— лінійно незалежні і утворюють базис. у певному базисі
у певному базисі  .
.
 —
—  -та координата вектора
-та координата вектора 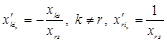 .
.
 — розклад у старому базисі. Отримаємо координати цього вектора
— розклад у старому базисі. Отримаємо координати цього вектора 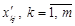 у новому базисі.
у новому базисі.

 .
.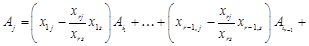

 .
. ,
,
 .
.
 ,
, .
. .
. ,
,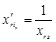 .
. будемо називати ведучим елементом, а
будемо називати ведучим елементом, а  — основним множником.
— основним множником. ;
;  —
— 
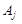
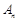

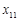





 ←
←

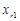
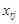


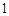








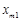



 з клітинкою
з клітинкою 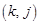 , а інша діагональ (додаткова) — клітинку
, а інша діагональ (додаткова) — клітинку  з клітинкою
з клітинкою 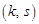 .
. .
. .
. утворюють базис даної системи векторів. Необхідно переконатися, що вектори
утворюють базис даної системи векторів. Необхідно переконатися, що вектори  також утворюють базис і знайти координати усіх векторів у новому базисі.
також утворюють базис і знайти координати усіх векторів у новому базисі.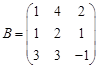 .
. ,
,
 - вектор-стовпець
- вектор-стовпець  - обернена матриця до базисної матриці
- обернена матриця до базисної матриці  - вектор-стовпець шуканих координат вектора
- вектор-стовпець шуканих координат вектора  .
. .
. :
: ,
, .
. вектором
вектором  знову приводить до базису. Згідно леми 1.4.1, для цього достатньо перевірити відмінність від нуля координати вектора
знову приводить до базису. Згідно леми 1.4.1, для цього достатньо перевірити відмінність від нуля координати вектора  :
:  .
. і ведучий елемент
і ведучий елемент  .
. у новому базисі будуть такими:
у новому базисі будуть такими: ,
, ,
, ,
, ,
, ,
, .
.

 .
.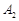
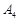





 ←
←




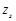 таку суму
таку суму або
або  . Тоді оцінкою вектора
. Тоді оцінкою вектора  .
. — базисний вектор, що займає
— базисний вектор, що займає  -те місце у базисі, то для цього вектора
-те місце у базисі, то для цього вектора  і
і  .
. , що серед координат вектора
, що серед координат вектора  є додатні, тоді базис, якому відповідає кращий базисний розв’язок (з більшим значенням цільової функції), отримується заміною вектором
є додатні, тоді базис, якому відповідає кращий базисний розв’язок (з більшим значенням цільової функції), отримується заміною вектором  .
. — невироджений базисний розв’язок. Не обмежуючи загальності припустимо, що перші
— невироджений базисний розв’язок. Не обмежуючи загальності припустимо, що перші  і
і  — базис базисного розв’язку,
— базис базисного розв’язку,  — відповідне значення цільової функції. Оскільки розв’язок допустимий, тоді
— відповідне значення цільової функції. Оскільки розв’язок допустимий, тоді .
. (за нашим припущенням
(за нашим припущенням  ), тоді замінюючи вектор
), тоді замінюючи вектор  у базисі на
у базисі на 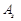 , ми знову отримаємо базис
, ми знову отримаємо базис 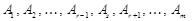 .
.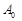 у новому базисі будуть:
у новому базисі будуть: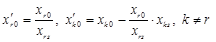 ,
, — координати вектора
— координати вектора 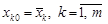 .
. , де
, де 
 , а інші координати нульові, був невиродженим необхідно, щоб
, а інші координати нульові, був невиродженим необхідно, щоб  .
. , маємо
, маємо  . Якщо для якогось
. Якщо для якогось 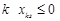 , то
, то  також.
також. , то
, то 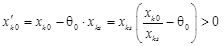 (згідно умови теореми). Тобто, новий базисний розв’язок невироджений.
(згідно умови теореми). Тобто, новий базисний розв’язок невироджений.

 .
.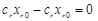 і згрупувавши доданки, дістанемо:
і згрупувавши доданки, дістанемо: .
. .
. і
і  , то
, то 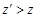 , що і треба було довести.
, що і треба було довести. ; або є
; або є  для якого всі
для якого всі  ; або є оцінка
; або є оцінка  , для якої є
, для якої є  виконуються для декількох
виконуються для декількох 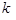 ?
? , то цей розв’язок оптимальний.
, то цей розв’язок оптимальний. — базисний розв’язок,
— базисний розв’язок,  — його базис і
— його базис і  , тобто
, тобто  .
. .
. .
. і
і  , то
, то .
.
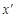 — допустимий розв’язок, то
— допустимий розв’язок, то .
. і
і
 .
. — також допустимий розв’язок, то
— також допустимий розв’язок, то .
. .
. ,
, така, що для неї всі
така, що для неї всі 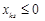 , то це означає, що цільова функція ЗЛП не обмежена зверху на допустимій множині.
, то це означає, що цільова функція ЗЛП не обмежена зверху на допустимій множині. — базисний розв’язок, для якого виконані умови теореми, і
— базисний розв’язок, для якого виконані умови теореми, і  .
. ,
,  де
де 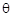 - довільне додатне число.
- довільне додатне число.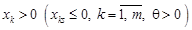 і, крім того, задовольняє обмеженням задачі, тобто є допустимим для даної ЗЛП. Дійсно
і, крім того, задовольняє обмеженням задачі, тобто є допустимим для даної ЗЛП. Дійсно .
.
 .
.
 , то згідно (1.4.13) цільову функцію можна збільшувати необмежено, залишаючись у допустимій області. Теорему доведено.
, то згідно (1.4.13) цільову функцію можна збільшувати необмежено, залишаючись у допустимій області. Теорему доведено. , а
, а  .
.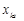 є додатні, але
є додатні, але  досягається не при одному, а при декількох значеннях
досягається не при одному, а при декількох значеннях 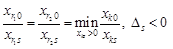 .
. і
і  , то отримаємо знову базис незалежно від того, виведемо з базису вектор
, то отримаємо знову базис незалежно від того, виведемо з базису вектор  чи
чи  . Нехай, наприклад, замінимо вектор
. Нехай, наприклад, замінимо вектор  .
. і
і  . Але при
. Але при  маємо
маємо  , бо
, бо  .
. ) дорівнює нулю. А це вступає у протиріччя з припущенням невиродженості задачі.
) дорівнює нулю. А це вступає у протиріччя з припущенням невиродженості задачі. і, таким чином, розв’язок оптимальний.
і, таким чином, розв’язок оптимальний. . Тоді задача не має оптимального розв’язку. Її цільова функція не обмежена зверху на допустимій множині.
. Тоді задача не має оптимального розв’язку. Її цільова функція не обмежена зверху на допустимій множині. .
.


