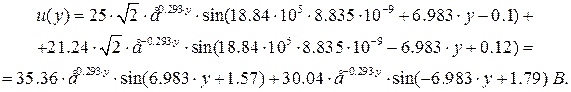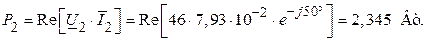Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розрахунок магнітних кіл постійного струму
Приклад 1. Знайти магнітну індукцію (magnetic induction) в повітряному зазорі магнітного кола (рисунок 2.30), якщо І=2 А, w=300, b1=40 мм, b2=20 мм, h=200мм, a=180 мм, d=30 мм, d=0,2 мм. Крива намагнічування задана аналітичним виразом: H=aB3, де a=600A/mT3. Розв’язування. Визначаємо число ділянок магнітного кола, для чого розбиваємо магнітопровід (magnetic core) на ділянки однакового перерізу. Таких ділянок в прикладі, що розглядається, три (таблиця 2.3).
Таблиця 2.3 –Параметри ділянок магнітного кола
Зобразимо схему електричного кола, розрахунок якої аналогічний розрахунку даного магнітного кола (рисунок 2.31). Коло містить два нелінійних резистори (nonlinear resistor), які відповідають двом ділянкам магнітного кола, і один лінійний, який відповідає повітряному зазорові. Оскільки коло складається тільки з послідовно з’єднаних резисторів, то, знаючи вебер-амперні характеристики (weber-ampere characteristic) ділянок кола і, додавши їх по осі абсцис, можна отримати вебер-амперну характеристику всього кола.
Визначимо вебер-амперні характеристики ділянок і результати наведемо в таблицях 2.3, 2.4, 2.5. Значення B і H отримаємо з аналітичного виразу кривої намагнічування. Якщо ця залежність наведена у вигляді графіка, то В і відповідне йому значення Н визначається безпосередньо з графіка. При визначенні вебер-амперної характеристики ділянки l2-3, тобто повітряного зазору, потрібно пам’ятати, що магнітна проникність повітря m0 – величина постійна і тому
В=m0Н, де m0=4p×10-7 Г/м. Таблиця 2.4 - Ділянка l1-2
Таблиця 2.5 - Ділянка l3-1
Оскільки вебер-амперна характеристика повітряного зазору являє собою пряму лінію, яка проходить через початок координат, то достатньо знайти лише одну точку цієї прямої.
Наприклад, В=1 Т. H=B/m0=795×103 A/м; Ф=BS2-3=0.6 мВб; Um=Hl2-3=159 A.
Отримані таким чином вебер-амперні характеристики будуємо на одному графіку в одному масштабі (рисунок 2.32) і знаходимо вебер-амперну характеристику всього кола. Потім за цією характеристикою і відомою намагнічувальною силою Iw=600 визначаємо величину магнітного потоку (magnetic flux) в магнітопроводі Ф=0,88 мВб. Магнітна індукція в зазорі:
В=Ф/S2-3=1,47 T.
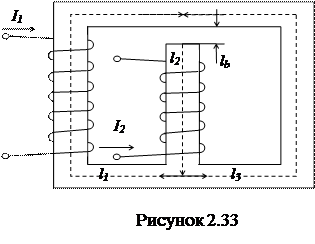
Приклад 2. На осерді із електротехнічної сталі знаходяться дві обмотки з числами витків W1=300 і W2=75, по якому проходить струми I1= 1,5A та I2= 2,0А заданого напрямку (рисунок 2.33). Довжини середніх магнітних ліній окремих ділянок однакового перерізу l1=l3=49см, l2=22,5см. Перерізи ділянок S1=S2=S3=3×10-3м2. Довжина повітряного проміжку ld=0,5мм. Крива намагнічування задана в таблиці 2.6. Знайти значення магнітних потоків у стержнях осердя.
Таблиця 2.6.
Розв’язування. Зобразимо магнітне коло у вигляді його аналога-нелінійного електричного кола (рисунок 2.34). Для цього вибираємо додатні напрямки магнітних потоків Ф у стержнях осердя і визначаємо напрямки магніторушійних сил, створених струмами обмоток. Для розрахунку застосуємо метод двох вузлів. За першим законом Кірхгофа для схеми рисунка 2.34 запишемо вираз
При цьому Магнітні потоки Ф1, Ф2, Ф3, зобразимо у вигляді функцій вузлової напруги
Задаємося значеннями магнітної індукції В і напруженості (intensity) магнітного кола Н з таблиці 2.6. знаходимо значення магнітних потоків за формулою Ф = В S і магнітних напруг за формулою:
Напруженість магнітного поля в повітряному проміжку знаходимо за формулою: За даними таблиці 2.7 будуємо вебер-амперні характеристики
Перевіримо правильність, розрахунку за рівняннями Кірхгофа:
(-4,55+1,75+2,8)×10-3=0 Таблиця 2.7 - Результати розрахунків
Знаходимо значення магнітної індукції:
За значеннями магнітної індукції знаходимо напруженість Ні в кожному стержні осердя, використовуючи для цього криву B=f(H). Знаходимо напруженість магнітного поля в повітряному проміжку:
Отримані значення
складені за 2-м законом Кірхгофа для схеми рисунка 2.34. При правильному розрахунку рівняння (5,6), як і рівняння (1), перетворюються в тотожності.
Рисунок 2.35 Розрахунок довгої лінії Приклад 1. Диспетчерський зв'язок здійснюється по повітряній лінії на частоті 300 кГц. Первинні параметри лінії зв'язку (communication line):
Лінія навантажена на опір Необхідно: 1) визначити хвильовий опір (wave impedance), коефіцієнт поширення, фазову швидкість і довжину хвилі; 2) обчислити коефіцієнти відбиття за напругою і струмом від кінця лінії і коефіцієнти біжучої і стоячої хвиль; 3) побудувати графіки розподілу миттєвих значень прямої, зворотної і сумарної хвиль напруги і струму вздовж лінії довжиною 4) визначити діючі значення напруги і струму на початку лінії; 5) визначити потужність, що витрачається в лінії і розвивається генератором. Розв’язування 1. Для лінії з втратами
Хвильовий опір Коефіцієнт поширення (propagation factor)
коефіцієнт згасання (damping factor) коефіцієнт фази (phase factor) Фазова швидкість (phase velocity) Довжина хвилі (wave length) 1. Коефіцієнти відбиття (reflectivity) за напругою і струмом:
Коефіцієнт біжучої хвилі (travelling wave factor):
Коефіцієнт стоячої хвилі (standing wave ratio):
3. Розподіл миттєвих значень напруги і струму вздовж лінії при
Струм в навантаженні:
Оскільки При
Отримаємо рівняння хвиль напруги і струму, в яких одна змінна ¾ поточна координата
Для побудови графіків миттєвих значень падаючих, відбитих і сумарних хвиль напруги і струму визначаємо їх значення в точках лінії з мінімальним інтервалом. Комплекси діючих значень напруги і струму на початку лінії при
Потужність, яка розвивається в генераторі:
Потужність навантаження:
Графіки показані на рисунках 2.36 і 2.37.
Рисунок 2.36
Рисунок 2.37 Потужність, втрачена в лінії:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 731; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.171.121 (0.043 с.) |




 (1)
(1)
 . Тоді для кожної ділянки магнітного кола можна записати:
. Тоді для кожної ділянки магнітного кола можна записати: (2)
(2) (3)
(3) (4)
(4)
 . Результати розрахунків занесені в таблицю 2.7.
. Результати розрахунків занесені в таблицю 2.7. (криві 1-3 на рисунку 2.35). Отримаємо сумарну криву 4, точка перетину якої з абсцисою графіка (точка Р) дає розв'язок системи рівнянь (1-4). Ордината, проведена через точку Р, перетинає криві 1, 2, 3 в точках
(криві 1-3 на рисунку 2.35). Отримаємо сумарну криву 4, точка перетину якої з абсцисою графіка (точка Р) дає розв'язок системи рівнянь (1-4). Ордината, проведена через точку Р, перетинає криві 1, 2, 3 в точках  які визначають магнітні потоки
які визначають магнітні потоки 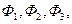 за величиною та напрямком. З рисунка 2.35 маємо:
за величиною та напрямком. З рисунка 2.35 маємо: 



 .
. необхідно підставити в рівняння:
необхідно підставити в рівняння: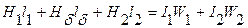 , (5)
, (5) (6)
(6)

 . Напруга на навантаженні
. Напруга на навантаженні 
 для моменту t, при якому напруга падаючої хвилі в кінці лінії максимальна;
для моменту t, при якому напруга падаючої хвилі в кінці лінії максимальна;



 .
.


 .
.
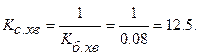
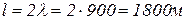



 в кінці лінії, фаза цієї напруги
в кінці лінії, фаза цієї напруги  .
. в кінці лінії
в кінці лінії
 :
: