
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Балаш О.С., Высочанская Е.Ю.,Стр 1 из 5Следующая ⇒
Балаш О.С., Высочанская Е.Ю., Попова А.А. Б20Методы оптимальных решений: методические указания /О.С. Балаш, Е.Ю. Высочанская, А.А. Попова – Саратов: Изд-во Сарат. ин-та РГТЭУ, 2011. – 42 с.
В данном пособии в краткой форме излагаются основные положения учебного материала по прикладной математике, приводятся решения типовых задач. Для студентов 1 и 2 курсов, обучающихся на заочной форме обучения в Саратовском институте (филиале) РГТЭУ. Методические указания предназначены для студентов, обучающихся по направлению 080100.62 «Экономика»
УДК 51 ББК 22.1
Согласовано: Зав. библиотекой_________Е.А. Лазарева
© Саратовский институт РГТЭУ, 2011
Оглавление Введение. 4 Линейное программирование. 5 1. Элементы линейной алгебры.. 5 2. Основные понятия линейного программирования. 6 3. Геометрическое решение задач линейного программирования. 8 4. Симплексный метод. 13 4.1. Решение производственной задачи симплексным методом.. 17 5. Транспортная задача. 21 5.1. Математическая модель и анализ транспортной задачи. 22 5.2. Составление начального плана перевозок. 24 5.3. Распределительный метод решения транспортной задачи. 26 5.4 Метод потенциалов. 33 5.5 Особенности решения транспортной задачи с невыполненным балансом 37 Литература. 39 а) основная литература. 39 б) дополнительная литература. 39
Введение Высшая и прикладная математика является фундаментальной общеобразовательной дисциплиной в системе подготовки специалистов в области экономики, менеджмента, товароведения и коммерции. В результате изучения курса прикладной математики студент должен овладеть основными понятиями, идеями и методами математики для решения экономических, управленческих и коммерческих задач. Особое внимание уделяется практическому применению основных математических понятий и методов при решении типовых задач коммерции и экономики. Курс “Прикладная математика” содержит элементы математического программирования. Цель предлагаемого материала - оказать помощь студентам-заочникам в их самостоятельной работе по изучению курса “Прикладной математики”.
Линейное программирование Математическое программирование представляет собой математическую дисциплину, занимающуюся изучением экстремальных задач и разработкой методов их решения.
Элементы линейной алгебры
Определение. Упорядоченная совокупность n действительных чисел называется n - мерным вектором `a = (a 1, a 2, …, an). Определение. аi называется i-компонентой вектора a. Определение. Нулевой вектор – это вектор, каждая компонента которого равна нулю. Определение. i-й единичный вектор – этовектор, i -я компонента которого равна единице, а остальные нули: ` li = (0,0,…,1,…,0). Определение. Сумма двух векторов – это вектор, каждая компонента которого представляет собой сумму соответствующих компонент этих векторов. ` Определение. Вектор Определение. Вектор (– Матрицы и действия над ними Определение. Прямоугольная таблица чисел размерности m´n, где m – число строк, n – число столбцов, называется прямоугольной матрицей размера m´n A = Например, матрица А размером 2´3:
Определение. Матрица называется квадратной порядка n, если ее число строк и столбцов совпадает, то есть m = n. Например, квадратная матрица А размером 4´4: A = Определение. Единичной матрицей называется квадратная матрица, у которой на главной диагонали стоят единицы, а остальные элементы – нули. Е = Определение. Нулевой матрицей называется квадратная матрица, все элементы которой равны 0.
Основные понятия линейного программирования Определение. Общей задачей линейного программирования называется задача, которая состоит в определении максимума (минимума) целевой функции Z (x 1, ...xn) = c 1 x 1 +...+cnxn при ограничениях:
xj Определение. Функция (1) называется целевой функцией или линейной формой задачи линейного программирования, а условия (2) – (4) – ограничениями данной задачи. Определение. Стандартной (симметричной) задачей линейного программирования называется задача, которая состоит в определении экстремального значения целевой функции (1) при выполнении условий (2) и (4).
Определение. Основной (канонической) задачей линейного программирования называется задача, которая состоит в определении экстремального значения целевой функции (1) при выполнении условий (3) и (4). Определение. Вектор или совокупность чисел Определение. План `Х*= (х 1*, х 2 *, ...., хn*), при котором целевая функция (1) принимает свое оптимальное (минимальное или максимальное) значение, называется оптимальным планом. Таким образом, линейное программирование является частью математического программирования, особенностью которого является то, что исследуемая целевая функция является линейной: Z (x 1, ...,xn) = c 1 x 1 +...+cnxn, а ограничения, накладываемые на переменные, представляют собой линейные уравнения или неравенства. Если же целевая функция или система ограничений нелинейная, то соответствующая задача является задачей нелинейного программирования. Если требуется провести поиск целочисленных значений xj, то приходим к задаче целочисленного линейного программирования (ЦЛП).
3. Геометрическое решение задач
Геометрическое решение задач линейного программирования приемлемо для случаев n Как известно, линейное уравнение a 1 x 1 +a 2 x 2 = b задает на плоскости (в пространстве R 2) прямую; уравнение a 1 x 1 + a 2 x 2 + a 3 x 3 = b – плоскость в R 3. Точно так же уравнение ai 1 x 1 +... + ainxn = bi (i -ое ограничение в канонической задаче ЛП) определяет в пространстве Rn некоторое множество, называемое гиперплоскостью. Определение. Фигура на плоскости называется выпуклой, если наряду с любыми ее точками М 1 и М 2 ей принадлежат и все точки отрезка М 1 М 2. Например, отрезок, треугольник, квадрат, острый угол. Определение. Множество X называется выпуклым, если вместе с любыми двумя точками (элементами) (x 1, y 1);(x 2, y 2)
Это уравнение является уравнением отрезка. Теорема. Пересечение любого числа выпуклых множеств является выпуклым множеством. Очевидно, прямая в R 2, плоскость в R 3 являются выпуклыми множествами. Точно так же, выпуклым множеством является гиперплоскость ai 1 x 1 +... + ainxn = bi и полупространство (вместе с границей) в Rn, определяемое i -м ограничением в стандартной задаче: ai1x1 +... + ainxn £ bi. Система ограничений (2) задает множество М – пересечение m выпуклых множеств в n -мерном евклидовом пространстве Rn, поэтому само является выпуклым множеством. Множество М называется выпуклым многогранником (областью) допустимых решений. При наличии только двух переменных М задает многоугольник решений в R 2, а в случае переменных x 1, x 2, x 3 – выпуклый многогранник в пространстве R 3. Геометрическое решение задачи линейного программирования состоит в том, что из всех допустимых решений требуется выделить оптимальное решение, определяющее экстремум целевой функции Z. Теорема. Функция цели (1) задачи линейного программирования достигает экстремума в угловой точке выпуклого множества допустимых решений. Решить задачу графически – значит найти угловую точку выпуклого множества области допустимых решений, координаты которой дают экстремум функции цели.
Симплексный метод
Алгебраический метод решения (симплекс-метод) разработан американским математиком Д. Данцигом и опубликован в 1951 году. В его основе лежит использование элементарных преобразований матрицы ограничений канонической задачи линейного программирования (метод Жордана-Гаусса). Переход от общей задачи линейного программирования (1), (2), (4) к задаче в канонической форме (1), (3), (4), осуществляется с помощью введения m неотрицательных дополнительных переменных
которые удовлетворяют системе линейных уравнений:
и дают экстремум функции цели:
Правомерность перехода от общей задачи к задаче в канонической форме основывается на теореме: неотрицательное решение системы неравенств (2) является решением системы уравнений (6). Справедливо и обратное утверждение. Рассмотрим задачу линейного программирования на нахождение минимума целевой функции. Справедливы теоремы. Теорема 1. Если для некоторого фиксированного индекса j выполняется условие Zj – cj > 0, то можно построить хотя бы один опорный план, для которого значение целевой функции Z будет меньше первоначального, то есть Z < Z0. Теорема 2. Если для некоторого опорного плана` x выполняется соотношение Zj – cj £ 0, то план` x является оптимальным. Сформулируем алгоритм симплексного метода. По условию задачи составляется экономико-математическая модель задачи в общем виде: Z (x 1, ..., xn) = c 1 x 1 +...+cnxn
xj Переходят от задачи на максимум к задаче на минимум Z. Для этого целевую функцию умножают на (–1). – Z(x 1,..., xn) = – c 1 x 1– ... – cnxn От общей задачи линейного программирования с помощью дополнительных переменных переходят к задаче в канонической форме.
xj Запишем систему ограничений в векторной форме:
или
Составляется первая симплексная таблица: Таблица 1
Столбец «Базис» – столбец векторов, входящих в базис.
Столбец «C» – столбец коэффициентов, стоящих в целевой функции при векторах базиса. Строка «Zj – cj» – называется индексной строкой. Столбец «b» – столбец ограничений по ресурсам, входящих в базис. Столбцы a 1 … am, …, am+ 1, …, an – это коэффициенты, стоящие при неизвестных в системе ограничений. Заполним индексную строку «Zj – cj». Для столбца «b» это значение равно сумме попарных произведений элементов столбца «C» на элементы столбца «b», т. е.
Решение находится в столбце «b»:
Две верхние строки таблицы содержат коэффициенты функции цели и n+m векторов системы ограничений. Просматриваются числа Zj – cj индексной строки. В задаче требуется найти минимум функции цели, следовательно, базисное решение будет минимальным, при условии, что все числа индексной строки отрицательные или нули. Если же среди чисел индексной строки есть хотя бы одно положительное, то план не оптимальный и его следует улучшить. Предположим, что базисное решение не оптимальное. Из всех положительных чисел индексной строки выбирается наибольшее по абсолютной величине, то есть Определяем направляющую (ведущую) строку. Определяется число После выбора разрешающего элемента симплексная таблица преобразовывается по формулам прямоугольника:
aij – разрешающий элемент матрицы, aij После преобразования получим: Элементы, участвующие в процедуре преобразования, являются вершинами прямоугольника, причем в одной из них обязательно находится разрешающий элемент aij. После преобразования элементов исходной симплексной таблицы вновь просматривают числа индексной строки. Если эти числа отрицательны или равны нулю, то базисное решение оптимальное, и процесс преобразования симплексной таблицы прекращается. Если же решение не оптимальное, то процесс преобразования симплексной таблицы повторяется. Симплексный метод повторяют до тех пор, пока не будет найдено базисное решение.
4.1. Решение производственной задачи
Требуется найти максимум функции доходов: Z = 4 x 1 + 6 x 2 при ограничениях:
Сведем задачу на максимум к задаче на минимум. Для этого умножим функцию цели на (–1). – Z = –4 x 1 – 6 x 2 Для приведения задачи к каноническому виду (с ограничениями-равенствами), пригодному к решению симплекс-методом, вводим дополнительные неотрицательные переменные x 3, x 4, x 5 Имеем: – Z = –4 x 1 – 6 x 2 + 0 х 3 + 0 х 4 + 0 х 5
В производственной задаче дополнительные переменные x 3, x 4, x 5 означают количество неиспользованного сырья (остаток) соответственно первого, второго и третьего вида. Запишем задачу в векторной форме: – Z = –4 x 1 – 6 x 2 + 0 х 3 + 0 х 4 + 0 х 5
Составим первую симплекс-таблицу (таблица 2). Коэффициенты при дополнительных переменных x 3, x 4, x 5 образуют единичную матрицу. Принимаем вектора коэффициентов при x 3, x 4, x 5 за базис, то есть в столбец «Базис» записываем вектора В столбец С запишем коэффициенты, стоящие в целевой функции при соответствующих переменных (в нашем случае они равны нулю). В столбец b поставим ограничения по ресурсам. Коэффициенты в столбцах а 1, а 2, …а 5 – это коэффициенты, соответствующие переменным х 1, х 2,… х 5 в системе ограничений, записанной в векторной форме. Последняя строка называется индексной. Ее заполняют следующим образом. Находят сумму попарных произведений столбца b на С, затем вычитают соответствующий коэффициент при целевой функции. Столбец b: Z 0=0×784 + 0×552 + 0×567 = 0. Столбец а 1: Z 1 – c 1 = 0×16 + 0×8 + 0×5 – (– 4) = 4. Столбец а 2: Z 2 – c 2 = 0×4 +0×7 + 0×6 – (– 6) = 6. Столбец а 3: Z 3 – c 3 = 0×1 +0×0 + 0×0 – 0 = 0 Столбец а 4: Z 4 – c 4 = 0×0 + 0×1 + 0×0 – 0 = 0 Столбец а 5: Z 5 – c 5 = 0×0 + 0×0 + 0×1– 0 = 0 Полученные значения записываем в индексную строку таблицы 2. Таблица 2
Первое базисное решение находится в столбце b: x 1 = 0; x 2 = 0; x 3 = 784; x 4 = 552; x 5 = 567. При этом Z = 0. В индексной строке имеются положительные числа 4, 6. Следовательно, план не оптимальный. Применяем алгоритм симплексного метода. 1. Выбираем максимальный по абсолютной величине элемент, стоящий в индексной строке. Этот элемент равен 6. Ему соответствует столбец а 2. Этот столбец будем называть направляющим. Выделим его в симплексной таблице. 2. Выбираем направляющую строку. Для этого делим элементы столбца b на соответствующие числа направляющего столбца и находим минимальное частное, то есть
Минимальное частное соответствует третьей строке. Таким образом, направляющей строкой будет строка а 5. Выделим ее. Если в направляющем столбце стоят нули или отрицательные числа, то соответствующие строки не рассматриваются. Если все элементы столбца меньше или равны нулю, то нельзя выбрать направляющую строку и найти оптимальное решение. 3. Элемент, стоящий на пересечении направляющей строки и направляющего столбца называется разрешающим. В данном случае он равен 9. 4. Строим вторую симплексную таблицу. Для этого переменную, соответствующую разрешающему столбцу а 2 введем в базис на место переменной а 5. 5. Элементы направляющей строки делим на разрешающий и результаты вносим в соответствующую строку второй симплекс-таблицы. То есть в третьей строке второй симплексной таблицы (таблица 3), получим: (63; 5/9; 1; 0; 0; 1/9). 6. Элементы направляющего столбца, кроме разрешающего, равного теперь единице, заменяем нулями. Результат вносим в соответствующий столбец новой таблицы. 7. Все остальные элементы преобразуем по правилу прямоугольника. Для этого для каждого элемента исходной таблицы составим прямоугольник так, чтобы преобразуемый элемент и разрешающий располагались на одной из диагоналей прямоугольника. Преобразованное значение вычисляют по формуле (8): строка а3:
строка а 4:
индексная строка:
Полученные значения записываем на соответствующие места таблицы 3. Таблица 3
Получили второе базисное решение: x 1 = 0; x 2 = 63; x 3 = 532; x 4 = 111; x 5 = 0и– Z 2 = –378(значение –378 находится на пересечении индексной строки и столбца из свободных членов). Это решение не оптимально, так как в индексной строке имеется положительное число 2/3. Повторяем процедуру симплексного метода. Выбираем направляющий столбец (положительное число в индексной строке соответствует а 1). Вводим в базис вектор а 1 в новой симплекс-таблице.
Выбираем направляющую строку, то есть находим:
Направляющей строкой будет строка а4. Разрешающий элемент 37/9. Составим третью симплекс-таблицу (табл.4). Таблица 4.
Получили третье базисное решение: x 1 = 27; x 2 = 48; x 3 = 16; x 4 = 0; x 5 = 0; -Z=- 396. В индексной строке нет положительных чисел. Решение оптимальное. Вывод. Для получения максимальной стоимости готовой продукции Zmax =396 руб. необходимо изготовить 27 единиц продукции вида A и 48 единиц продукции вида В. При этом сырье первого вида останется неизрасходованным в количестве x 3 = 16 кг, а сырье второго и третьего вида будет израсходовано полностью x 4 = 0; x 5 = 0. Заметим, что ранее тот же результат был получен геометрическим методом решения.
Транспортная задача Транспортная задача является специальной задачей линейного программирования. Имеется m баз (пунктов отправления) A 1, A 2,..., A m, в которых сосредоточены запасы однородного груза в количествах Определение. Транспортная задача называется задачей с выполненным балансом или транспортной задачей закрытого вида, если запасы груза на базах совпадают с потребностями потребителей, то есть
Рассмотрим закрытую модель транспортной задачи с матрицей перевозок, заданной в таблице 5. Таблица 5
5.1. Математическая модель и анализ
Обозначим xij – величина груза, перевозимого с базы Ai (i= 1,2,…, m) потребителю Bj (j= 1,2,…, n). Так как стоимости перевозок cij (тарифы) известны, запишем функцию общих затрат на перевозку:
Величина перевозимых грузов не может быть отрицательна:
Если задача с выполненным балансом, то есть выполняется условие (9), то количество вывозимого с i -ой базы груза должно совпадать с запасами на этой базе:
количество груза, перевозимого j -ому потребителю, должно совпадать с его потребностями
Математическая модель задачи: требуется минимизировать функцию затрат (функцию цели) Z:
При наличии ограничений:
Отметим следующие особенности транспортной задачи: 1. Все коэффициенты в системе ограничений равны единице. 2. Не все m + n уравнений являются независимыми. В силу условия При решении транспортной задачи выделяются следующие шаги: 1. Составление начального плана перевозок. 2. Проверка плана на оптимальность и его пошаговое улучшение. Метод потенциалов
Метод потенциалов является одним из наиболее часто используемых методов уточнения плана перевозок. Каждой строке с номером i в матрице перевозок приписывается числовое значение
где Определение. Сумма потенциалов для свободных клеток называется косвенными тарифами
Соотношение между косвенными тарифами свободных клеток базисного решения и их истинными (заданными тарифами) служат критериями оптимальности решения. Теорема. Достаточное условие оптимальности. Если для всех свободных клеток таблицы перевозок Если есть свободные клетки, для которых Алгоритм решения транспортной задачи Пусть имеется исходное базисное решение. 1. Для каждой строки и столбца матрицы перевозок необходимо задать потенциалы и для каждой базисной (заполненной) клетки записать уравнение вида (16). Получим систему уравнений для потенциалов. 2. Так как заполненных клеток 3. Для каждой свободной строки находят косвенный тариф 4. Если косвенный тариф больше истинного, то переходят к пункту 5. Если косвенный тариф меньше или равен истинному тарифу, то данное базисное решение является оптимальным. 5. Среди разностей между косвенным и истинным тарифами, найденных в пункте 3, выбирают наибольшую. Находят соответствующую ей свободную клетку. 6. Для свободной клетки строят цикл перечета. По нему производят сдвиг, преобразовав свободную клетку в базисную. Получают новое базисное решение. 7. Возвращаются к пункту 1 алгоритма. Литература а) основная литература 1. Акулич И.Л. Математическое программирование в решениях и задачах: Учебное пособие для студентов экономических специальностей ВУЗов - М.: Высшая школа,1986 2.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 355; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.195.110 (0.204 с.) |


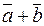 =(a 1+ b 1, a 2+ b 2,…, an + bn).
=(a 1+ b 1, a 2+ b 2,…, an + bn). , умноженный на число l называется произведением вектора a на число, если каждая компонента вектора
, умноженный на число l называется произведением вектора a на число, если каждая компонента вектора 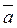 = (la 1, la 2,…, la n).
= (la 1, la 2,…, la n). .
.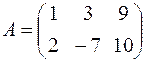 .
.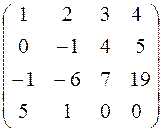 .
. .
. max (min) (1)
max (min) (1)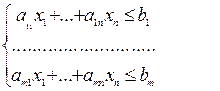 (2)
(2) (3)
(3) 0, (j = 1, …, n). (4)
0, (j = 1, …, n). (4)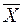 = (х 1, х 2, ...., хn), удовлетворяющих ограничениям задачи (2) – (4), называется допустимым решением или планом задачи линейного программирования.
= (х 1, х 2, ...., хn), удовлетворяющих ограничениям задачи (2) – (4), называется допустимым решением или планом задачи линейного программирования. 3.
3.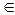 X оно содержит отрезок между этими точками, т.е. точки вида
X оно содержит отрезок между этими точками, т.е. точки вида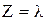 y+ (1 –
y+ (1 – 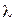 ) x, (0
) x, (0  ,
,  ,
,  . Эти переменные добавляются к каждому из неравенств системы (2), обращая их в равенства, и входят в функцию цели с коэффициентами, равными нулю. В этом случае задача линейного программирования в канонической форме формулируется так: требуется найти совокупность неотрицательных чисел
. Эти переменные добавляются к каждому из неравенств системы (2), обращая их в равенства, и входят в функцию цели с коэффициентами, равными нулю. В этом случае задача линейного программирования в канонической форме формулируется так: требуется найти совокупность неотрицательных чисел , (5)
, (5) (6)
(6) max (min) (7)
max (min) (7) max
max


 0,(j = 1, …, n+m).
0,(j = 1, …, n+m).
 .
. .
. =(b 1, b 2, …, bm,0,…, 0); Z = Z0..
=(b 1, b 2, …, bm,0,…, 0); Z = Z0.. . Индекс j, которому соответствует такое число индексной строки, укажет вектор, который следует ввести в базис. Пусть им будет
. Индекс j, которому соответствует такое число индексной строки, укажет вектор, который следует ввести в базис. Пусть им будет  . Столбец, соответствующий этому вектору, будет направляющим (ведущим).
. Столбец, соответствующий этому вектору, будет направляющим (ведущим). . С этой целью компоненты базисного решения делятся на положительные компоненты ведущего вектора-столбца. Индекс i, которому соответствует
. С этой целью компоненты базисного решения делятся на положительные компоненты ведущего вектора-столбца. Индекс i, которому соответствует  , укажет вектор, который следует исключить из базиса. Пусть им будет вектор
, укажет вектор, который следует исключить из базиса. Пусть им будет вектор 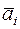 . Строка, соответствующая этому вектору, будет направляющей (ведущей). Элемент xij, стоящий на пересечении ведущего столбца и ведущей строки, называется разрешающим элементом.
. Строка, соответствующая этому вектору, будет направляющей (ведущей). Элемент xij, стоящий на пересечении ведущего столбца и ведущей строки, называется разрешающим элементом. , (8)
, (8) 0.
0. , все остальные элементы в столбце с разрешающим элементом преобразуются в нули. Тем самым, в соответствующей системе линейных уравнений неизвестное xj останется с коэффициентом, равным единице в i -м уравнении, а во всех остальных будет исключено.
, все остальные элементы в столбце с разрешающим элементом преобразуются в нули. Тем самым, в соответствующей системе линейных уравнений неизвестное xj останется с коэффициентом, равным единице в i -м уравнении, а во всех остальных будет исключено.

 .
. .
. .
. ;
;  ;
;  ;
;  ;
;  .
. ;
;  ;
;  ;
;  ;
;  .
. ;
;  ;
;  ;
; 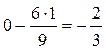 .
. .
. соответственно. Груз необходимо перевезти n потребителям (магазинам) B 1, B 2,..., B n в количествах
соответственно. Груз необходимо перевезти n потребителям (магазинам) B 1, B 2,..., B n в количествах  соответственно. Известна стоимость
соответственно. Известна стоимость  перевозки единицы груза с базы Ai (i= 1,2,…, m) потребителю Bj (j= 1,2,…, n). Требуется спланировать перевозки грузов так, чтобы их общая стоимость была минимальная.
перевозки единицы груза с базы Ai (i= 1,2,…, m) потребителю Bj (j= 1,2,…, n). Требуется спланировать перевозки грузов так, чтобы их общая стоимость была минимальная. . (9)
. (9)
 min. (10)
min. (10) (i= 1,2,…, m)(j= 1,2,…, n). (11)
(i= 1,2,…, m)(j= 1,2,…, n). (11) , (12)
, (12)
 . (13)
. (13) min (14)
min (14) (15)
(15) одно из ограничений можно исключить и тогда для общего числа m´n переменных будет m + n –1 ограничений. То есть опорный план должен содержать не более m + n –1 компонент. В этом случае план называется невырожденным. В случае вырожденного опорного плана число компонент будет меньше, чем m + n –1. Если план оказывается вырожденным, то в клетку следует ввести пустую поставку (груз, равный 0) и считать ее заполненной.
одно из ограничений можно исключить и тогда для общего числа m´n переменных будет m + n –1 ограничений. То есть опорный план должен содержать не более m + n –1 компонент. В этом случае план называется невырожденным. В случае вырожденного опорного плана число компонент будет меньше, чем m + n –1. Если план оказывается вырожденным, то в клетку следует ввести пустую поставку (груз, равный 0) и считать ее заполненной.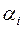 , а каждому столбцу с номером j значение
, а каждому столбцу с номером j значение 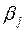 .
. 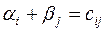 , (16)
, (16) – тариф перевозки.
– тариф перевозки. .
. . (17)
. (17) , то этот план будет оптимальным, причем если
, то этот план будет оптимальным, причем если  , для всех свободных клеток, оптимальный план единственный. Если для некоторых пустых клеток
, для всех свободных клеток, оптимальный план единственный. Если для некоторых пустых клеток 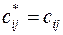 , то оптимальный план не единственный.
, то оптимальный план не единственный. , то рассматриваемый план перевозок не является оптимальным и может быть улучшен пересчетом по циклу, соответствующему одной из клеток, в которых
, то рассматриваемый план перевозок не является оптимальным и может быть улучшен пересчетом по циклу, соответствующему одной из клеток, в которых 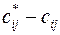 будет максимальной).
будет максимальной). , то соотношение (16) задают систему
, то соотношение (16) задают систему 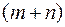 неизвестными. Дополняя ее условием:
неизвестными. Дополняя ее условием:  , получают единственное решение системы потенциалов. Числа
, получают единственное решение системы потенциалов. Числа 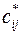 .
.


