
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 1. Производственная задача
Предприятие производит продукцию двух видов А и В, для производства которых используется сырье трех видов. На изготовление единицы изделия А требуется затратить сырья каждого вида 16, 8 и 5 кг соответственно, а для единицы изделия В – 4, 7 и 9 кг. Производство обеспечено сырьем каждого вида в количестве 784 кг, 552 кг и 567 кг соответственно. Стоимость единицы изделия А составляет 4 руб., единицы изделия В – 6 руб. Требуется составить план производства изделий А и В, обеспечивающий максимальную стоимость готовой продукции. Решить исходную задачу геометрически. Решение. Дадим математическую постановку задачи. Пусть продукции А производится x 1 единиц, а продукции В – x 2единиц. Стоимость всех изделий А составит 4 х 1 рублей, изделий В –6 х 2рублей, суммарная стоимость произведенной продукции: Z = 4 x 1 + 6 x 2. Требуется затратить 16 x 1 кг – количество сырья первого вида, идущего на изготовление всех изделий вида A; 4 x 2 – количество сырья первого вида, идущего на изготовление всех изделий вида B. Получим ограничение по сырью первого вида: 16 x 1 + 4 x 2 £ 784. Аналогично определяем ограничение по сырью 2 вида: 8 x 1 + 7 x 2 £ 552, и ограничение по сырью 3 вида: 5 x 1 + 9 x 2 £ 567. Количество выпускаемых изделий не может быть отрицательным. Следовательно, получаем условие неотрицательности решения: x 1 ³ 0, x 2 ³ 0. Таким образом, получили задачу линейного программирования: Требуется максимизировать функцию стоимости готовой продукции: Z = 4 x 1 + 6 x 2 при ограничениях:
Решим задачу графически. Так как переменные x 1, x 2 неотрицательны, то допустимые решения лежат в первом координатном углу. Для построения области допустимых решений (ОДР) для каждого ограничения строят прямую, соответствующую равенству. Первому условию в системе ограничений соответствует равенство: 16 x 1 + 4 x 2 = 784. Построим эту прямую по точкам:
Прямая разбивает плоскость на две полуплоскости. Для определения искомой полуплоскости берут произвольную точку, не принадлежащую прямой, и проверяют, удовлетворяют ли ее координаты рассматриваемому неравенству. Если удовлетворяют, то все точки полуплоскости, которому принадлежит взятая точка, есть решение данного неравенства. В противном случае рассматриваемому неравенству удовлетворяют все точки другой полуплоскости, которой не принадлежит выбранная точка.
Если прямая не проходит через начало координат, то в качестве произвольно выбранной точки удобно брать начало координат, то есть точку О (0, 0). Для нашего случая возьмем начало координат О (0; 0) и, поставив ее координаты в неравенство, получим: 16×0 + 4×0 < 784. Имеем верное равенство. Следовательно, полуплоскость, которой принадлежит точка О (0, 0) и есть геометрическое решение неравенства. Решением первого неравенства системы является полуплоскость, лежащая ниже прямой 16 x 1 + 4 x 2= 784. Таким же образом найдем решения каждого неравенства системы (рис. 1). Решением системы неравенств будет пересечение всех полуплоскостей. Это пересечение есть выпуклое множество, называемое областью допустимых решений(ОДР). В общем случае, ОДР может быть замкнутым выпуклым многоугольником, незамкнутым или пустым. Для нахождения оптимального решения, то есть такого, при котором целевая функция принимает свое максимальное (минимальное) значение, дадим целевой функции Z произвольное численное значение, то есть положим Z = С (стоимость постоянная). Множество точек 4 x 1 + 6 x 2 = С определяет прямую, называемой линией уровня функции цели Z (x 1, x 2). При различных значениях С получаем семейство линий уровня – параллельных прямых с одним и тем же нормальным вектором Интерес представляют линии уровня, имеющие общие точки с ОДР. При С = 0 общая стоимость равна нулю. Так как коэффициенты функции цели Z положительны, ее значение увеличивается при движении прямых от линии уровня, проходящей через точку O (0,0), в направлении вектора Координатами нормального вектора являются коэффициенты при текущих координатах в уравнении прямой Z, то есть
Рис.1. Геометрическое решение задачи линейного программирования
Из рисунка видно, что точкой, в которой прямая Z касается ОДР является точка А. Находим ее координаты, решая систему уравнений:
Получим x 1 = 27, x 2= 48, то есть точка А имеет координаты (27; 48). Максимальный доход составляет Zmax = 4∙27 + 6∙48 = 396руб. Ответ. Для получения максимальной стоимости изделий Z = 396 рублей необходимо изготовить изделий А x 1 = 27 единиц, изделий В x 2 = 48 единиц. При геометрическом решении задач линейного программирования следует знать следующие свойства: 1. Если оптимальное решение существует, то оно лежит на границе ОДР. 2. Если решение единственное, то оно достигается в одной из вершин ОДР. 3. Если решений множество, то они достигаются на одной из сторон выпуклого многоугольника ОДР. 4. Решение, лежащее в одной из вершин ОДР, является опорным решением, а сама вершина – опорной точкой. 5. Для того, чтобы найти опорное решение достаточно перебрать все вершины ОДР (опорные точки) и выбрать ту, где целевая функция достигает максимума (минимума).
Симплексный метод
Алгебраический метод решения (симплекс-метод) разработан американским математиком Д. Данцигом и опубликован в 1951 году. В его основе лежит использование элементарных преобразований матрицы ограничений канонической задачи линейного программирования (метод Жордана-Гаусса). Переход от общей задачи линейного программирования (1), (2), (4) к задаче в канонической форме (1), (3), (4), осуществляется с помощью введения m неотрицательных дополнительных переменных
которые удовлетворяют системе линейных уравнений:
и дают экстремум функции цели:
Правомерность перехода от общей задачи к задаче в канонической форме основывается на теореме: неотрицательное решение системы неравенств (2) является решением системы уравнений (6). Справедливо и обратное утверждение. Рассмотрим задачу линейного программирования на нахождение минимума целевой функции. Справедливы теоремы. Теорема 1. Если для некоторого фиксированного индекса j выполняется условие Zj – cj > 0, то можно построить хотя бы один опорный план, для которого значение целевой функции Z будет меньше первоначального, то есть Z < Z0. Теорема 2. Если для некоторого опорного плана` x выполняется соотношение Zj – cj £ 0, то план` x является оптимальным. Сформулируем алгоритм симплексного метода. По условию задачи составляется экономико-математическая модель задачи в общем виде: Z (x 1, ..., xn) = c 1 x 1 +...+cnxn
xj Переходят от задачи на максимум к задаче на минимум Z. Для этого целевую функцию умножают на (–1). – Z(x 1,..., xn) = – c 1 x 1– ... – cnxn От общей задачи линейного программирования с помощью дополнительных переменных переходят к задаче в канонической форме.
xj Запишем систему ограничений в векторной форме:
или
Составляется первая симплексная таблица:
Таблица 1
Столбец «Базис» – столбец векторов, входящих в базис. Столбец «C» – столбец коэффициентов, стоящих в целевой функции при векторах базиса. Строка «Zj – cj» – называется индексной строкой. Столбец «b» – столбец ограничений по ресурсам, входящих в базис. Столбцы a 1 … am, …, am+ 1, …, an – это коэффициенты, стоящие при неизвестных в системе ограничений. Заполним индексную строку «Zj – cj». Для столбца «b» это значение равно сумме попарных произведений элементов столбца «C» на элементы столбца «b», т. е.
Решение находится в столбце «b»:
Две верхние строки таблицы содержат коэффициенты функции цели и n+m векторов системы ограничений. Просматриваются числа Zj – cj индексной строки. В задаче требуется найти минимум функции цели, следовательно, базисное решение будет минимальным, при условии, что все числа индексной строки отрицательные или нули. Если же среди чисел индексной строки есть хотя бы одно положительное, то план не оптимальный и его следует улучшить. Предположим, что базисное решение не оптимальное. Из всех положительных чисел индексной строки выбирается наибольшее по абсолютной величине, то есть Определяем направляющую (ведущую) строку. Определяется число После выбора разрешающего элемента симплексная таблица преобразовывается по формулам прямоугольника:
aij – разрешающий элемент матрицы, aij После преобразования получим:
Элементы, участвующие в процедуре преобразования, являются вершинами прямоугольника, причем в одной из них обязательно находится разрешающий элемент aij. После преобразования элементов исходной симплексной таблицы вновь просматривают числа индексной строки. Если эти числа отрицательны или равны нулю, то базисное решение оптимальное, и процесс преобразования симплексной таблицы прекращается. Если же решение не оптимальное, то процесс преобразования симплексной таблицы повторяется. Симплексный метод повторяют до тех пор, пока не будет найдено базисное решение.
4.1. Решение производственной задачи Требуется найти максимум функции доходов: Z = 4 x 1 + 6 x 2 при ограничениях:
Сведем задачу на максимум к задаче на минимум. Для этого умножим функцию цели на (–1). – Z = –4 x 1 – 6 x 2 Для приведения задачи к каноническому виду (с ограничениями-равенствами), пригодному к решению симплекс-методом, вводим дополнительные неотрицательные переменные x 3, x 4, x 5 Имеем: – Z = –4 x 1 – 6 x 2 + 0 х 3 + 0 х 4 + 0 х 5
В производственной задаче дополнительные переменные x 3, x 4, x 5 означают количество неиспользованного сырья (остаток) соответственно первого, второго и третьего вида. Запишем задачу в векторной форме: – Z = –4 x 1 – 6 x 2 + 0 х 3 + 0 х 4 + 0 х 5
Составим первую симплекс-таблицу (таблица 2). Коэффициенты при дополнительных переменных x 3, x 4, x 5 образуют единичную матрицу. Принимаем вектора коэффициентов при x 3, x 4, x 5 за базис, то есть в столбец «Базис» записываем вектора В столбец С запишем коэффициенты, стоящие в целевой функции при соответствующих переменных (в нашем случае они равны нулю). В столбец b поставим ограничения по ресурсам. Коэффициенты в столбцах а 1, а 2, …а 5 – это коэффициенты, соответствующие переменным х 1, х 2,… х 5 в системе ограничений, записанной в векторной форме. Последняя строка называется индексной. Ее заполняют следующим образом. Находят сумму попарных произведений столбца b на С, затем вычитают соответствующий коэффициент при целевой функции. Столбец b: Z 0=0×784 + 0×552 + 0×567 = 0. Столбец а 1: Z 1 – c 1 = 0×16 + 0×8 + 0×5 – (– 4) = 4. Столбец а 2: Z 2 – c 2 = 0×4 +0×7 + 0×6 – (– 6) = 6. Столбец а 3: Z 3 – c 3 = 0×1 +0×0 + 0×0 – 0 = 0 Столбец а 4: Z 4 – c 4 = 0×0 + 0×1 + 0×0 – 0 = 0 Столбец а 5: Z 5 – c 5 = 0×0 + 0×0 + 0×1– 0 = 0 Полученные значения записываем в индексную строку таблицы 2. Таблица 2
Первое базисное решение находится в столбце b: x 1 = 0; x 2 = 0; x 3 = 784; x 4 = 552; x 5 = 567. При этом Z = 0. В индексной строке имеются положительные числа 4, 6. Следовательно, план не оптимальный. Применяем алгоритм симплексного метода.
1. Выбираем максимальный по абсолютной величине элемент, стоящий в индексной строке. Этот элемент равен 6. Ему соответствует столбец а 2. Этот столбец будем называть направляющим. Выделим его в симплексной таблице. 2. Выбираем направляющую строку. Для этого делим элементы столбца b на соответствующие числа направляющего столбца и находим минимальное частное, то есть
Минимальное частное соответствует третьей строке. Таким образом, направляющей строкой будет строка а 5. Выделим ее. Если в направляющем столбце стоят нули или отрицательные числа, то соответствующие строки не рассматриваются. Если все элементы столбца меньше или равны нулю, то нельзя выбрать направляющую строку и найти оптимальное решение. 3. Элемент, стоящий на пересечении направляющей строки и направляющего столбца называется разрешающим. В данном случае он равен 9. 4. Строим вторую симплексную таблицу. Для этого переменную, соответствующую разрешающему столбцу а 2 введем в базис на место переменной а 5. 5. Элементы направляющей строки делим на разрешающий и результаты вносим в соответствующую строку второй симплекс-таблицы. То есть в третьей строке второй симплексной таблицы (таблица 3), получим: (63; 5/9; 1; 0; 0; 1/9). 6. Элементы направляющего столбца, кроме разрешающего, равного теперь единице, заменяем нулями. Результат вносим в соответствующий столбец новой таблицы. 7. Все остальные элементы преобразуем по правилу прямоугольника. Для этого для каждого элемента исходной таблицы составим прямоугольник так, чтобы преобразуемый элемент и разрешающий располагались на одной из диагоналей прямоугольника. Преобразованное значение вычисляют по формуле (8): строка а3:
строка а 4:
индексная строка:
Полученные значения записываем на соответствующие места таблицы 3. Таблица 3
Получили второе базисное решение: x 1 = 0; x 2 = 63; x 3 = 532; x 4 = 111; x 5 = 0и– Z 2 = –378(значение –378 находится на пересечении индексной строки и столбца из свободных членов). Это решение не оптимально, так как в индексной строке имеется положительное число 2/3. Повторяем процедуру симплексного метода. Выбираем направляющий столбец (положительное число в индексной строке соответствует а 1). Вводим в базис вектор а 1 в новой симплекс-таблице.
Выбираем направляющую строку, то есть находим:
Направляющей строкой будет строка а4. Разрешающий элемент 37/9. Составим третью симплекс-таблицу (табл.4). Таблица 4.
Получили третье базисное решение: x 1 = 27; x 2 = 48; x 3 = 16; x 4 = 0; x 5 = 0; -Z=- 396. В индексной строке нет положительных чисел. Решение оптимальное. Вывод. Для получения максимальной стоимости готовой продукции Zmax =396 руб. необходимо изготовить 27 единиц продукции вида A и 48 единиц продукции вида В. При этом сырье первого вида останется неизрасходованным в количестве x 3 = 16 кг, а сырье второго и третьего вида будет израсходовано полностью x 4 = 0; x 5 = 0. Заметим, что ранее тот же результат был получен геометрическим методом решения.
Транспортная задача Транспортная задача является специальной задачей линейного программирования. Имеется m баз (пунктов отправления) A 1, A 2,..., A m, в которых сосредоточены запасы однородного груза в количествах Определение. Транспортная задача называется задачей с выполненным балансом или транспортной задачей закрытого вида, если запасы груза на базах совпадают с потребностями потребителей, то есть
Рассмотрим закрытую модель транспортной задачи с матрицей перевозок, заданной в таблице 5. Таблица 5
5.1. Математическая модель и анализ
Обозначим xij – величина груза, перевозимого с базы Ai (i= 1,2,…, m) потребителю Bj (j= 1,2,…, n). Так как стоимости перевозок cij (тарифы) известны, запишем функцию общих затрат на перевозку:
Величина перевозимых грузов не может быть отрицательна:
Если задача с выполненным балансом, то есть выполняется условие (9), то количество вывозимого с i -ой базы груза должно совпадать с запасами на этой базе:
количество груза, перевозимого j -ому потребителю, должно совпадать с его потребностями
Математическая модель задачи: требуется минимизировать функцию затрат (функцию цели) Z:
При наличии ограничений:
Отметим следующие особенности транспортной задачи: 1. Все коэффициенты в системе ограничений равны единице. 2. Не все m + n уравнений являются независимыми. В силу условия При решении транспортной задачи выделяются следующие шаги: 1. Составление начального плана перевозок. 2. Проверка плана на оптимальность и его пошаговое улучшение.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1450; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.40.207 (0.114 с.) |
 max
max
 . С увеличением Z они будут передвигаться в одну сторону, с уменьшением – в противоположную.
. С увеличением Z они будут передвигаться в одну сторону, с уменьшением – в противоположную. . Крайняя прямая из семейства параллельных прямых имеет с многоугольником решений общую точку А.
. Крайняя прямая из семейства параллельных прямых имеет с многоугольником решений общую точку А. (4; 6). Поэтому для определения оптимального плана на графике достаточно построить нормальный вектор
(4; 6). Поэтому для определения оптимального плана на графике достаточно построить нормальный вектор 

 ,
,  ,
,  . Эти переменные добавляются к каждому из неравенств системы (2), обращая их в равенства, и входят в функцию цели с коэффициентами, равными нулю. В этом случае задача линейного программирования в канонической форме формулируется так: требуется найти совокупность неотрицательных чисел
. Эти переменные добавляются к каждому из неравенств системы (2), обращая их в равенства, и входят в функцию цели с коэффициентами, равными нулю. В этом случае задача линейного программирования в канонической форме формулируется так: требуется найти совокупность неотрицательных чисел , (5)
, (5) (6)
(6) max (min) (7)
max (min) (7)
 0, (j = 1,…, n)
0, (j = 1,…, n)

 0,(j = 1, …, n+m).
0,(j = 1, …, n+m).
 .
. .
. =(b 1, b 2, …, bm,0,…, 0); Z = Z0..
=(b 1, b 2, …, bm,0,…, 0); Z = Z0.. . Индекс j, которому соответствует такое число индексной строки, укажет вектор, который следует ввести в базис. Пусть им будет
. Индекс j, которому соответствует такое число индексной строки, укажет вектор, который следует ввести в базис. Пусть им будет  . Столбец, соответствующий этому вектору, будет направляющим (ведущим).
. Столбец, соответствующий этому вектору, будет направляющим (ведущим). . С этой целью компоненты базисного решения делятся на положительные компоненты ведущего вектора-столбца. Индекс i, которому соответствует
. С этой целью компоненты базисного решения делятся на положительные компоненты ведущего вектора-столбца. Индекс i, которому соответствует  , укажет вектор, который следует исключить из базиса. Пусть им будет вектор
, укажет вектор, который следует исключить из базиса. Пусть им будет вектор 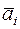 . Строка, соответствующая этому вектору, будет направляющей (ведущей). Элемент xij, стоящий на пересечении ведущего столбца и ведущей строки, называется разрешающим элементом.
. Строка, соответствующая этому вектору, будет направляющей (ведущей). Элемент xij, стоящий на пересечении ведущего столбца и ведущей строки, называется разрешающим элементом. , (8)
, (8) 0.
0. , все остальные элементы в столбце с разрешающим элементом преобразуются в нули. Тем самым, в соответствующей системе линейных уравнений неизвестное xj останется с коэффициентом, равным единице в i -м уравнении, а во всех остальных будет исключено.
, все остальные элементы в столбце с разрешающим элементом преобразуются в нули. Тем самым, в соответствующей системе линейных уравнений неизвестное xj останется с коэффициентом, равным единице в i -м уравнении, а во всех остальных будет исключено.
 .
. .
. .
. ;
;  ;
;  ;
;  ;
;  .
. ;
;  ;
;  ;
;  ;
;  .
. ;
;  ;
;  ;
; 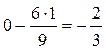 .
. .
. соответственно. Груз необходимо перевезти n потребителям (магазинам) B 1, B 2,..., B n в количествах
соответственно. Груз необходимо перевезти n потребителям (магазинам) B 1, B 2,..., B n в количествах  соответственно. Известна стоимость
соответственно. Известна стоимость  перевозки единицы груза с базы Ai (i= 1,2,…, m) потребителю Bj (j= 1,2,…, n). Требуется спланировать перевозки грузов так, чтобы их общая стоимость была минимальная.
перевозки единицы груза с базы Ai (i= 1,2,…, m) потребителю Bj (j= 1,2,…, n). Требуется спланировать перевозки грузов так, чтобы их общая стоимость была минимальная. . (9)
. (9)
 min. (10)
min. (10) (i= 1,2,…, m)(j= 1,2,…, n). (11)
(i= 1,2,…, m)(j= 1,2,…, n). (11) , (12)
, (12)
 . (13)
. (13) min (14)
min (14) (15)
(15) одно из ограничений можно исключить и тогда для общего числа m´n переменных будет m + n –1 ограничений. То есть опорный план должен содержать не более m + n –1 компонент. В этом случае план называется невырожденным. В случае вырожденного опорного плана число компонент будет меньше, чем m + n –1. Если план оказывается вырожденным, то в клетку следует ввести пустую поставку (груз, равный 0) и считать ее заполненной.
одно из ограничений можно исключить и тогда для общего числа m´n переменных будет m + n –1 ограничений. То есть опорный план должен содержать не более m + n –1 компонент. В этом случае план называется невырожденным. В случае вырожденного опорного плана число компонент будет меньше, чем m + n –1. Если план оказывается вырожденным, то в клетку следует ввести пустую поставку (груз, равный 0) и считать ее заполненной.


