
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристика рядів розподілу
Для аналізу рядів розподілу одиниць сукупності визначаємо коефіцієнт асиметрії та коефіцієнт ексцесу. Коефіцієнт асиметрії показує скошеність кривої нормального закону розподілу вправо чи вліво по осі 0х.
де МО – модальне значення ознаки; s ‑ середньоквадратичне відхилення. Якщо А<0, то скошеність буде лівостороння. Якщо А>0, то скошеність буде правосторонньою. Якщо А=0 – розподіл симетричний. Для нормального розподілу характерним є те, що середня арифметична, мода і медіана рівні між собою. Для асиметричного розподілу характерні деякі розбіжності: - при правосторонній асиметрії - при лівосторонній асиметрії Коефіцієнт ексцесу характеризує гостровершність вершини розподілу, скупченість варіантів навколо середньої арифметичної.
де s ‑ середньоквадратичне відхилення; m ‑ центральний момент розподілу.
де Xi – індивідуальне значення ознаки; n- загальна сума частот усіх інтервалів. Якщо Е>3, то вершина кривої розподілу гостроверха. Якщо Е»3 – нормальна крива. Якщо Е<3 ‑ вершина кривої розподілу тупа. Визначимо показники ряду розподілу, який характеризує кількісну ознаку (первинну вартість) одиниць ОВФ по первинній вартості. А= Оскільки, А=0,73, тобто А>0, то крива розподілу буде мати правосторонню скошеність, а це означає, що розподіл асиметричний. Для того, щоб розрахувати коефіцієнт ексцесу розрахуємо спочатку µ 4 та σ4 µ 4= σ 4= (σ 2)2=( Е=127,69/295,8=0,8 Оскільки Е=0,8, тобто Е<3, то крива має тупу вершину, а це означає, що сукупність не однорідна. Визначимо показники ряду розподілу одиниць ОВФ по часу роботи А= Оскільки, А=0,8, тобто А>0, то крива розподілу буде мати правосторонню скошеність, а це означає, що розподіл асиметричний. Для того, щоб розрахувати коефіцієнт ексцесу розрахуємо спочатку µ 4 та σ4 µ 4= σ 4= (σ 2)2=( Е=89,13/133,7=0,6 Оскільки Е=0,6, тобто Е<3, то крива має тупу вершину, а це означає, що сукупність не однорідна. Перенесення результатів вибіркового спостереження на генеральну сукупність В даній роботі ми проводили статистичне дослідження по вибірковій сукупності, але необхідно зробити висновки по всій (генеральній) сукупності, визначивши і врахувавши помилку репрезентативності для середніх показників.
Для випадкового безповторного відбору середня помилка репрезентативності становить:
де s2 – дисперсія, квадрат середньоквадратичного відхилення; n – кількість одиниці вибіркової сукупності; N ‑ кількість одиниці генеральної сукупності. Гранична помилка репрезентативності, яка залежить від коефіцієнту довіри t: Dх = t*mх, де t = 1, t = 2, t = 3, що відповідають ймовірностям р = 0,683, р = 0,954, р = 0,997 відповідно. Розповсюдження результатів безповторного вибіркового спостереження на генеральну сукупність здійснюється методом прямого перерахування, коли узагальнюючий показник вибіркової сукупності множиться на кількість одиниць генеральної сукупності, враховуючи граничну помилку репрезентативності. Визначимо для первинної вартості середню помилку репрезентативності: mх = Гранична помилка репрезентативності при заданому коефіцієнті довіри t=3, з ймовірністю 0,997: Dх = 3*26,4=79,2 (тис. грн.)
Отже, обстеживши нашу сукупність з ймовірністю 0,997, ми можемо стверджувати, що середнє значення первинної вартості по всій сукупності буде знаходитись у інтервалі від Визначимо для залишкової вартостісередню помилку репрезентативності: mх = Гранична помилка репрезентативності при заданому коефіцієнті довіри t=3, з ймовірністю 0,997: Dх = 3*21,6=64,9 (тис. грн.)
Отже, обстеживши нашу сукупність з ймовірністю 0,997, ми можемо стверджувати, що середнє значення залишкової вартості по всій сукупності буде знаходитись у інтервалі від Визначимо для часу роботисередню помилку репрезентативності: mх = Гранична помилка репрезентативності при заданому коефіцієнті довіри t=3, з ймовірністю 0,997: Dх = 3*0,5=1,5 (год)
Отже, обстеживши нашу сукупність з ймовірністю 0,997, ми можемо стверджувати, що середнє значення часу роботи по всій сукупності буде знаходитись у інтервалі від
|
|||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 394; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.4.206 (0.012 с.) |

 (3.17)
(3.17) ‑ середнє значення ознаки;
‑ середнє значення ознаки; >Mе>Mo
>Mе>Mo (3.18)
(3.18) (3.19)
(3.19) ‑ середнє значення ознаки;
‑ середнє значення ознаки;
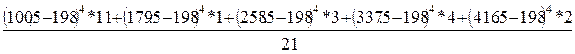 = 127,69 (грн4)
= 127,69 (грн4) )2=295,8 (грн4)
)2=295,8 (грн4)
 89,13(год4)
89,13(год4) )2=133,7
)2=133,7 (4.19)
(4.19) (тис. грн.)
(тис. грн.) (тис. грн.)
(тис. грн.) (тис. грн.)
(тис. грн.) (тис. грн.)
(тис. грн.)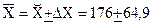 (тис. грн.)
(тис. грн.) (тис. грн.)
(тис. грн.) (год)
(год) (год)
(год) (годин)
(годин) 


