
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оцінювання основної похибки засобу вимірювання.
Методика визначення граничного значення основної похибки ЗВ залежить від способу її нормування та форми вираження класу точності ЗВ. Розглянемо основні випадки оцінювання основної похибки ЗВ. 1. Клас точності ЗВ, виражений у формі допустимої зведеної основної похибки gгр, яка є сталою в діапазоні вимірювання ЗВ (нормується адитивна похибка ЗВ).
де Dгр – границі допустимої абсолютної основної похибки; xN – нормувальне значення. Для характеристики класів точності аналогових (стрілкових) ЗВ використовують ряд чисел: (1; 1,5; 2; 2,5; 4; 5; 6) ´ 10 n, де n = 0, –1, –2… Ці значення затверджені Держстандартом.
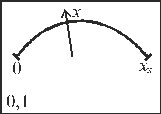
Рис. 1. Графічна інтерпретація похибок ЗВ для класу точності, вираженого у формі допустимої зведеної похибки. x Нта x К– нижня та верхня границі вимірювань відповідно. Як видно з рис. 1 границі допустимої абсолютної основної похибки Dгр не залежать від значення вимірюваної величини, а границі допустимої відносної похибки dгр зростають за гіперболічним законом при зменшенні x і зрівнюються з класом точності тільки в кінці діапазону вимірювання при x = xN чи x = xk: dгр = gгр. Якщо показ, наприклад, всередині шкали Отже, для забезпечення невеликих відносних похибок показів приладу, границю вимірювання х к необхідно вибрати так, щоб покази х були в другій половині, або в останній третині шкали. На рис. 2 а, б показані умовні зображення вимірювальних приладів з лінійною а) та нелінійною б) шкалами границі вимірювань, покази x та позначення класів точності
Рис. 2. Позначення класів точності. Приклад 1. За допомогою аналогового амперметра класу точності 0,5 з границею вимірювання I к = 10 А виконали два вимірювання струму і отримали покази: І 1 = 8,1 А та І 2 = 2,5 А. Визначити граничні значення основних абсолютної та відносної похибок для цих двох випадків і зробити висновок щодо точності виконаних вимірювань. Розв’язання. 1) Оскільки клас точності амперметра виражений у формі допустимої зведеної основної похибки gгр, яка дорівнює ± 0,5 %, то граничне значення абсолютної похибки Dгр є однаковим в обох вимірюваннях:
2) Граничне значення відносної основної похибки dгр залежить від показу амперметра:
Отже, точність вимірювання одним і тим самим приладом на цій самій границі залежить від того, наскільки отриманий показ близько чи далеко від границі вимірювання, і є вищою у першому випадку, коли I 1 = 8,1 А. 2. Клас точності ЗВ виражений у формі допустимої одночленної відносної похибки δгр (нормується мультиплікативна похибка ЗВ)
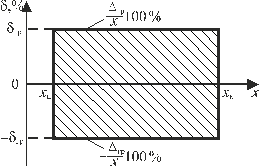
З формули видно, що при вираженні класу точності ЗВ у формі відносної похибки границі допустимої абсолютної похибки Dгр є лінійною функцією вимірюваної величини х. Клас точності δгр позначають числом в кружечку, наприклад
Рис. 3. Графічна інтерпретація похибок ЗВ для класу точності, вираженого у формі відносної похибки Приклад 2. Визначити інтервал, в якому може знаходитися істинне значення опору однозначної міри електричного опору класу точності Розв’язання. 1) Оскільки клас точності однозначної міри електричного опору виражений у формі допустимої відносної основної похибки dгр, яка дорівнює ± 0,02 %, то граничне значення абсолютної основної похибки D R гр відповідно до формули (**) дорівнює:
2) Істинне значення опору міри R може знаходитись в інтервалі R = (10,000 ± 0,002) Ом або від 9,998 Ом до 10,002 Ом.
3. Клас точності ЗВ виражений у формі допустимої двочленної відносної похибки δгр (нормується адитивна та мультиплікативна складові похибки ЗВ) і відображений двома числами c/d.
де
Рис. 4. Графічна інтерпретація похибок ЗВ для класу точності, вираженого у формі двочленної відносної похибки. Наприклад, якщо цифровий амперметр на границі вимірювання I к = 5 А має клас точності 0,5/0,2, то це означає, що граничне значення основної зведеної похибки
При відображенні класу точності ЗВ двома числами с / d границі допустимої абсолютної основної похибки Dгр лінійно зростають зі збільшенням вимірюваної величини х від якогось початкового значення Отже, внаслідок нормування границь похибок ЗВ з урахуванням адитивних і мультиплікативних складових при однакових похибках цифрового і аналогового приладів у кінці діапазону вимірювання (при х = х к) зі зменшенням показу х границі відносної похибки dгр цифрового приладу відповідно зростають не так швидко, як у аналогового приладу. Коефіцієнти c і d вибирають з ряду класів точності. Приклад 3. За допомогою цифрового амперметра класу точності 0,5/0,2 з границею вимірювання I к = 10 А виконали два вимірювання струму і отримали такі самі покази, як і для аналогового амперметра І 1 = 8,1 А та І 2 = 2,5 А. Визначити граничні значення основних абсолютної та відносної похибок для цих двох випадків і зробити висновок щодо точності вимірювань струму аналоговим та цифровим амперметрами при однакових показах І, однакових границях вимірювання І К та однакових граничних значеннях зведених похибок gгр у кінці діапазону вимірювання (якщо І = І к як у аналогового, так і у цифрового амперметрів gгр = ± 0,5 %). Розв’язання. За формулами для відносної та абсолютної похибок знайдемо:
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 480; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.214.32 (0.011 с.) |
 ;
; ;
; . (*)
. (*)


 , граничне значення відносної похибки зростає удвічі
, граничне значення відносної похибки зростає удвічі  , а при показі в одну десяту границі вимірювання
, а при показі в одну десяту границі вимірювання  – у десять разів
– у десять разів  .
.




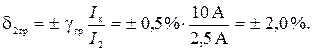
 ;
;  . (**)
. (**)
 – позначення
– позначення
 з номінальним значенням опору R н = 10 Ом.
з номінальним значенням опору R н = 10 Ом.
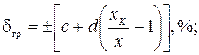

 – границя основної зведеної похибки в кінці діапазону вимірювання, коли x = x к, а
– границя основної зведеної похибки в кінці діапазону вимірювання, коли x = x к, а  – границя основної зведеної похибки на початку діапазону вимірювання, коли х = 0.
– границя основної зведеної похибки на початку діапазону вимірювання, коли х = 0.

 в кінці діапазону вимірювання при х = х к та
в кінці діапазону вимірювання при х = х к та  на початку діапазону вимірювання при х = 0.
на початку діапазону вимірювання при х = 0. , а границі допустимої відносної основної похибки dгр відповідно зменшуються за гіперболічним законом до значення dгр = ± с в кінці діапазону вимірювання.
, а границі допустимої відносної основної похибки dгр відповідно зменшуються за гіперболічним законом до значення dгр = ± с в кінці діапазону вимірювання. ;
; 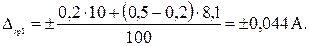
 ;
; 



