
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способи виявлення і усунення систематичних похибок
Результати спостережень, одержуваних при наявності систематичних похибок, називають невиправленими. При проведенні вимірювань намагаються виключити або врахувати вплив систематичних похибок. Цього можна досягнути таким чином: - виключенням джерел похибок до початку вимірювань; - визначенням поправок і внесенням їх в результат вимірювання; - оцінкою границь невиключених систематичних похибок. Зменшити постійну складову систематичної похибки можна такими методами: – метод заміщення, коли заміняють вимірювану величину відомою величиною, причому так, щоб в стані і діях всіх використаних засобів вимірювання не відбулось ніяких змін. Для реалізації цього методу потрібна регульована міра, величина якої однорідна до вимірюваної. Наприклад, вимірювання опору за допомогою моста постійного струму і мір опорів. - метод протиставлення, коли вимірювання виконується два рази і проводиться так, щоб в обох випадках причина постійної похибки чинила різні, але відомі по закономірності, впливи на результати спостережень. - метод компенсації похибки за знаком, коли проводиться вимірювання з двома спостереженнями, проведеними таким чином, щоб постійна систематична похибка входила в результат кожного з них з різними знаками. Наприклад, треба виміряти ЕРС потенціометром постійного струму, який має паразитну термо ЕРС. При проведенні одного вимірювання одержимо ЕРС Е 1. Змінимо полярність вимірюваної ЕРС і напрям струму в потенціометрі. Знову проведемо його зрівноваження – одержимо значення Е 2. - метод рандомізації – найбільш універсальний метод виключення невідомих постійних систематичних похибок. Одна і та сама величина вимірюється різними методами (приладами). Систематичні похибки кожного разу є різними випадковими величинами. Внаслідок цього при збільшенні числа використаних методів (приладів) систематичні похибки взаємокомпенсуються. Для виключення змінних систематичних похибок використовуються такі прийоми і методи: - Аналіз знаків невиправлених випадкових похибок. - Графічний метод. - Метод систематичних спостережень.
- Статичні методи.
Додавання похибок
Визначення шляхом розрахунку оцінки результуючої похибки за відомими оцінками її складових називається – додаванням похибок. Правила додавання похибок ґрунтуються на тому, що похибка по абсолютному значенню завжди набагато менша самої вимірювальної величини. Тому зміна похибки в важності від зміни вимірюваної величини може бути врахована, якщо випадкові і систематичні складові похибки розділити на адитивні і мультиплікативні. Сума адитивних складових дасть значення адитивної частини результуючої похибки, а сума мультиплікативних складових – значення мультиплікативної частини. При додаванні похибок треба враховувати, що: - окремі складові похибки можуть бути корельовано (взаємозалежні) між собою; - при додаванні випадкових величин їх закони розподілу значно деформуються, тобто форма закону суми може сильно відрізнятися від форми закону розподілу складових. Для виключення впливу деформації форми законів розподілу всі складові, які додаються, представляють своїми СКВ (d) і всі операції розрахункового додавання проводять тільки над ними. Врахування взаємних кореляційних зв’язків проводиться шляхом використання різних правил додавання для жорстко і слабо корельованих складових. Систематичні похибки, які незалежні одна від одної, додаються алгебраїчно з урахуванням їх знаків, а сумарна похибка визначається по модулю:
Незалежні випадкові похибки додаються геометрично:
При додаванні складових похибки з нормальним розподілом закон розподілу сумарної похибки також буде нормальним. Якщо складові похибки корельовано, то сумарна похибка визначається так:
де kij – коефіцієнт кореляції. Для двох корельованих похибок СКВ дорівнює:
Знаходження закону розподілу сумарної похибки при різних законах розподілу сумарної похибки при різних законах розподілу складових являє собою дуже важку задачу, в деяких випадках вона не розв’язана. ****
|
|||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 928; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.108.7 (0.004 с.) |
 . Значить систематична похибка, обумовлена дією термо ЕРС, усунена.
. Значить систематична похибка, обумовлена дією термо ЕРС, усунена. .
. і
і 

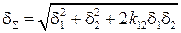 .
.


