
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная обратной функции
Пусть f: [ a, b ] → [ c, d ] непрерывная, строго монотонная на интервале [ a, b ] функция, имеющая производную в точке х 0
если f '(x 0) ≠ 0. Если f '(x 0) = 0, то g '(y 0) = + ∞ (в случае, когда f возрастает), и g '(y 0) = − ∞ (в случае, когда f убывает).
Производная сложной функции Пусть функция f: [ a, b ] → [ c, d ], а функция g:[ a 1, b 1] → [ c 1, d 1], причём [ a 1, b 1] g ' (f (x 0))· f ' (x 0). Производные тригонометрических функций Производные четырёх тригонометрических функций и, соответственно, четырёх обратных тригонометрических функций определяются следующими формулами (рядом указана область определения каждой функции):
35. Дифференциал, его геометрический смысл. Непрерывность. Дифференциал суммы, произведения и частного. Дифференциал сложной функции. Инвариантность формы дифференциала функций. Применение дифференциала к приближенным вычислениям. Дифференцирование неявных функций. Производные и дифференциалы высших порядков. Формула Лейбница(без доказательства).Механический смысл второй производной. Уравнение касательной и нормали к плоскости кривой. Дифференциал функции y=f(x) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dy (или df(x)). Иначе. Дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Правила дифференцирования суммы, произведения, частного функции. Производные сложных функций.
Для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу. Производная обратной функции равна обратной величине производной данной функции.
Неперывность ф-ции Пусть функция y=f(x) определена в точке х0 и в некоторой окрестности этой точки. Функция y=f(x) называется непрерывной в точке х0, если существует предел функции в этой точке и он равен значению функции в этой точке:
Это означает: - функция определена в точке х0 и в ее окрестности; - функция имеет предел при х→х0 - предел функции в точке х0 равен значению функции в этой точке, т.е. выполняется равенство. Это означает, что при нахождении предела непрерывной функции f(x) можно перейти к пределу под знаком функции, то есть в функции f(x) вместо аргумента х подставить предельное значение х0 дифференциалы высших порядков
36. Функции заданные параметрическими уравнениями их дифференцирование. Теоремы Коши, Лагранжа, Роля. Правило Лопиталя. 1) если При исследовании параметрически заданной функции иногда приходится находить ее производную по аргументу x. В этой статье мы выведем формулу производной параметрически заданной функции 2) Теорема Ролля Пусть функция f: [ a, b ] → R непрерывна на сегменте [ a, b ], и имеет конечную или бесконечную производную внутри этого сегмента. Пусть, кроме того, f (a) = f (b). Тогда внутри сегмента [ a, b ] найдется точка ξ такая, что f' (ξ) = 0.
Теорема Лагранжа Если функция f: [ a, b ] → R непрерывна на сегменте [ a, b ] и имеет конечную или бесконечную производную во внутренних точках этого сегмента, то
Теорема Коши Если каждая из функций f и g непрерывна на [ a, b ] и имеет конечную или бесконечную производную на ] a, b [ и если, кроме того, производная g' (x) ≠ 0 на ] a, b [, то
3) Правило Лопиталя представляет собой метод вычисления пределов, имеющих неопределенность
Пусть a является некоторым конечным действительным числом или равно бесконечности. · Если · Если Правило Лопиталя можно также применять к неопределенностям типа
Правило Лопиталя справедливо также и для односторонних пределов. Теоремы о возрастании и убывании (постоянстве) функций в интервале, достаточный признак. Выпуклость и вогнутость графика функции, точки перегиба. Необходимый признак существования точек перегиба. Достаточный признак существования точки перегиба. Теорема. Если в данном промежутке производная функции положительна, то функция возрастает в этом промежутке; если производная отрицательна, то функция убывает в соответствующем промежутке. Замечание. Теорема имеет простой геометрический смысл. Если в некотором промежутке касательная к графику функции у-/(х) образует с осью Ох острый угол а (18 а > 0), то функция возрастает в этом промежутке. Если касательная к графику образует с осью Ох тупой угол а (1§ сх < 0), то функция убывает. Достаточный признак возрастания функции. Если f’(х) > 0 в каждой точке интервала I, то функция f возрастает на I. Достаточный признак убывания функции. Если f’(х) < 0 в каждой точке интервала I, то функция f убывает на I. График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале. График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале. Теорема. Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f''(x) > 0 – вогнутый. Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба. Теорема. Пусть кривая определяется уравнением y = f(x). Если f ''(x0) = 0 или f ''(x0) не существует и при переходе через значение x = x0 производная f ''(x) меняет знак, то точка графика функции с абсциссой x = x0 есть точка перегиба. Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 302; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.107.255 (0.016 с.) |
 [ a, b ]. Тогда обратная функция g = f -1: [ c, d ] →[ a, b ] имеет производную в точке y 0 = f (x 0) интервала [ c, d ] равную
[ a, b ]. Тогда обратная функция g = f -1: [ c, d ] →[ a, b ] имеет производную в точке y 0 = f (x 0) интервала [ c, d ] равную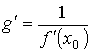 ,
,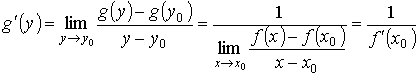 .
. [ c, d ]. Если функция f дифференцируема в точке х 0
[ c, d ]. Если функция f дифференцируема в точке х 0 











 Дифференциал n-ого порядка, есть дифференциал от дифференциала (n-1)-ого порядка, т.е. производную функции можно рассматривать, как отношение ее дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной.
Дифференциал n-ого порядка, есть дифференциал от дифференциала (n-1)-ого порядка, т.е. производную функции можно рассматривать, как отношение ее дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной. определены при
определены при  и существует обратная функция
и существует обратная функция  для
для  , то говорят о параметрическом задании функции
, то говорят о параметрическом задании функции  .
.

 такое, что f (b) - f (a) = f' (ξ)(b - a).
такое, что f (b) - f (a) = f' (ξ)(b - a).

 или
или  .
. и
и  , то
, то  ;
; и
и  , то аналогично
, то аналогично  . Первые две неопределенности
. Первые две неопределенности  можно свести к типу
можно свести к типу  сводятся к типу
сводятся к типу  с помощью соотношения
с помощью соотношения



