
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятия главного вектора и главного момента системы сил. Основная теорема статики. Условия равновесия произвольной системы сил.
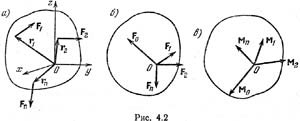
Пусть дана произвольная система сил (F1, F2,..., Fn). Сумму этих сил F=åFk называют главным вектором системы сил. Сумму моментов сил относительно какого-либо полюса называют главным моментом рассматриваемой системы сил относительно этого полюса. Оснтеор статики (теорема Пуансо): Всякую пространственную систему сил в общем случае можно заменить эквивалентной системой, состоящей из одной силы, приложенной в какой-либо точке тела (центре приведения) и равной главному вектору данной системы сил, и одной пары сил, момент которой равен главному моменту всех сил относительно выбранного центра приведения. При равновесии главный вектор системы равен нулю (
где Поскольку точка приведения выбрана произвольно, ясно, что при равновесии сумма моментов сил системы относительно любой точки на плоскости должна равняться нулю:
Эти точки не должны лежать на одной прямой. Условие равновесия произвольно плоской системы сил: Для того чтобы твердое тело под действием произвольной плоской системы сил находилось в равновесии, необходимо и достаточно, чтобы алгебраическая сумма моментов всех сил системы относительно любой точки в плоскости действия сил равнялось нулю. Алгебраический момент силы относительно точки. Алгебраический момент пары. Теорема Вариньона о моменте равнодействующей. Алгебраическим моментом силы относительно точки называют произведение модуля силы на плечо силы относительно этой точки (рис. 8), взятое со знаком плюс или минус. Плечом h силы
Если сила стремится вращать тело вокруг моментной точки против часовой стрелки, то берем знак плюс, если по часовой стрелке – знак минус. Алгебраический момент силы представляет собой произведение силы на длину (в СИ – Н∙м). Алгебраический момент силы не зависит от переноса силы вдоль ее линии действия. Алгебраический момент силы относительно точки равен нулю, если линия действия силы проходит через моментную точку. Алгебраический момент пары сил равен взятому с соответствующим знаком произведению модуля одной из сил пары на плечо пары: M=±F·d.
Правило знаков моментов пар сил аналогично правилу для моментов сил. Теорема Вариньона. Если плоская система сил приводится к равнодействующей, то момент этой равнодействующей относительно любого центра равен алгебраической сумме моментов всех сил системы относительно того же центра.
Понятие плоской системы сил. Уравнения равновесия произвольной плоской системы сил (три формы). Для равновесия произвольной плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы сумма проекций всех сил на каждую из двух прямоугольных осей, расположенных в плоскости действия сил, были равны нулю и сумма алгебраических моментов сил относительно любой точки, расположенной в плоскости действия сил, также была равна нулю:
Равенства (3.4) представляют так называемую основную форму условий равновесия при действии на тело плоской системы сил. Условия равновесия тела под действием плоской системы сил могут быть представлены еще в двух других формах. Вторая форма условий равновесия:
т. е. должны быть равны нулю суммы моментов сил относительно любых двух точек А, В, расположенных в плоскости действия сил, и сумма проекций всех этих сил на ось х (при этом ось х не должна быть перпендикулярна прямой АВ). Третья форма условий равновесия:
т. е. должны быть равны нулю суммы алгебраических моментов всех сил относительно любых трех точек А, В, С (эти точки расположены в плоскости действия сил и не лежат на одной прямой). Если на объект действует плоская система параллельных сил, условия равновесия выражаются двумя формами уравнений равновесия:
или
|
|||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 928; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.169.94 (0.006 с.) |
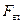 =0).
=0).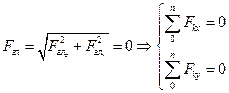
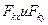 - проекция векторов на оси координат.
- проекция векторов на оси координат.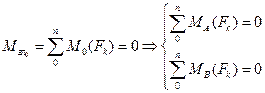 где А и В – разные точки приведения.
где А и В – разные точки приведения.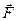 относительно точки называют кратчайшее расстояние между этой точкой и линией действия силы, т. е. длину отрезка перпендикуляра, опущенного из точки на линию действия силы
относительно точки называют кратчайшее расстояние между этой точкой и линией действия силы, т. е. длину отрезка перпендикуляра, опущенного из точки на линию действия силы 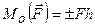 .
.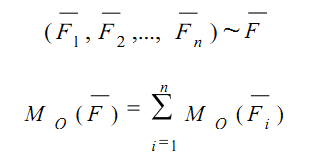
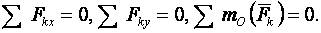 (3.4)
(3.4)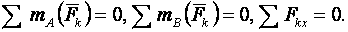 (3.5)
(3.5)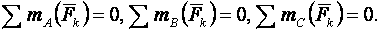 (3.6)
(3.6)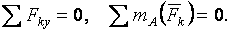 (3.7)
(3.7)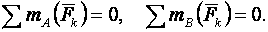 (3.8)
(3.8)


